Ratas framework: A comprehensive genai-based approach to rubric-based marking of real-world textual exams

Automated answer grading is a critical challenge in educational technology, with the potential to streamline assessment processes, ensure grading consistency, and provide timely feedback to students. However, existing approaches are often constrained to specific exam formats, lack interpretability in score assignment, and struggle with real-world applicability across diverse subjects and assessment types. To address these limitations, we introduce RATAS (Rubric Automated Tree-based Answer Scoring), a novel framework that leverages state-of-the-art generative AI models for rubric-based grading of textual responses. RATAS is designed to support a wide range of grading rubrics, enable subject-agnostic evaluation, and generate structured, explainable rationales for assigned scores. We formalize the automatic grading task through a mathematical framework tailored to rubric-based assessment and present an architecture capable of handling complex, real-world exam structures. To rigorously evaluate our approach, we construct a unique, contextualized dataset derived from real-world project-based courses, encompassing diverse response formats and varying levels of complexity. Empirical results demonstrate that RATAS achieves high reliability and accuracy in automated grading while providing interpretable feedback that enhances transparency for both students and nstructors.

An Approximation Approach for Solving the Subpath Planning Problem

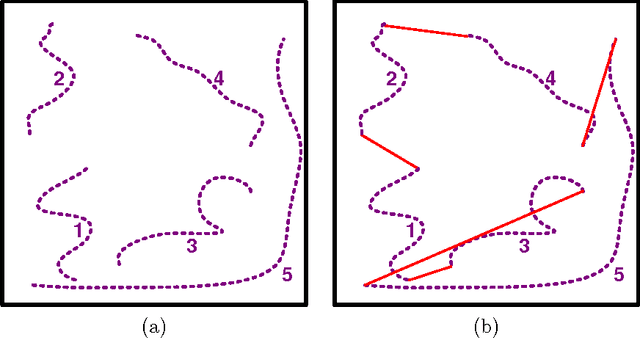
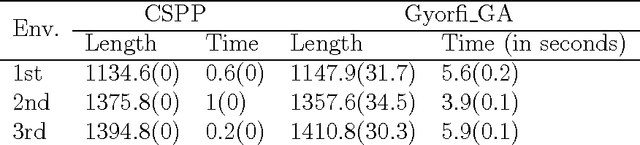
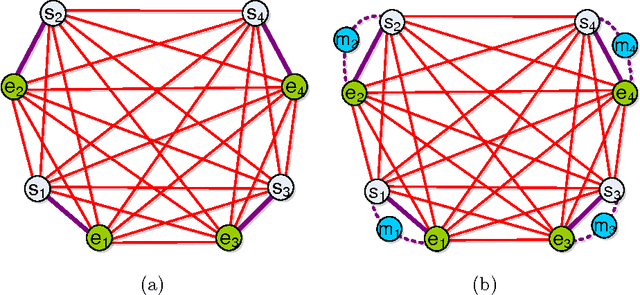
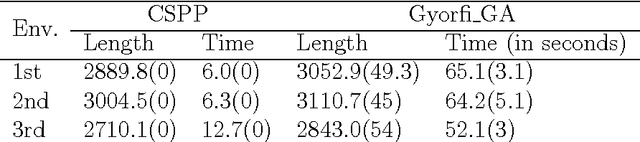
The subpath planning problem is a branch of the path planning problem, which has widespread applications in automated manufacturing process as well as vehicle and robot navigation. This problem is to find the shortest path or tour subject for travelling a set of given subpaths. The current approaches for dealing with the subpath planning problem are all based on meta-heuristic approaches. It is well-known that meta-heuristic based approaches have several deficiencies. To address them, we propose a novel approximation algorithm in the O(n^3) time complexity class, which guarantees to solve any subpath planning problem instance with the fixed ratio bound of 2. Also, the formal proofs of the claims, our empirical evaluation shows that our approximation method acts much better than a state-of-the-art method, both in result and execution time.