Mark N. Wegman
L2-Nonexpansive Neural Networks
Jul 03, 2018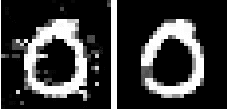
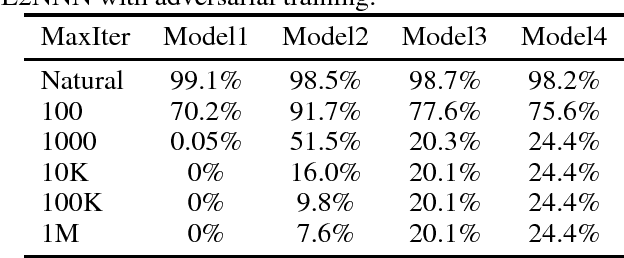
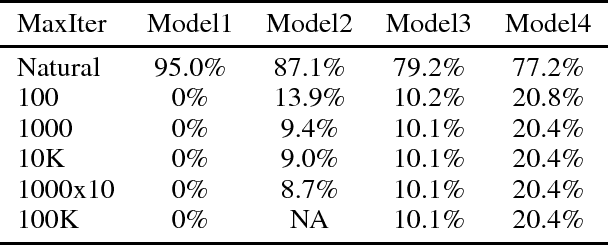
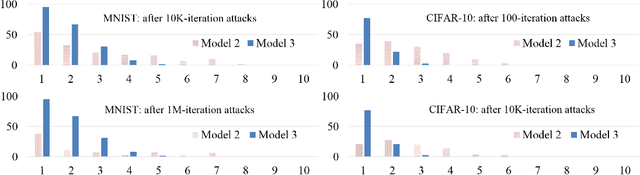
Abstract:This paper proposes a class of well-conditioned neural networks in which a unit amount of change in the inputs causes at most a unit amount of change in the outputs or any of the internal layers. We develop the known methodology of controlling Lipschitz constants to realize its full potential in maximizing robustness, with a new regularization scheme for linear layers, new ways to adapt nonlinearities and a new loss function. With MNIST and CIFAR-10 classifiers, we demonstrate a number of advantages. Without needing any adversarial training, the proposed classifiers exceed the state of the art in robustness against white-box L2-bounded adversarial attacks. Their outputs are quantitatively more meaningful than ordinary networks and indicate levels of confidence and generalization. They are also free of exploding gradients, among other desirable properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge