Adaptive generative moment matching networks for improved learning of dependence structures

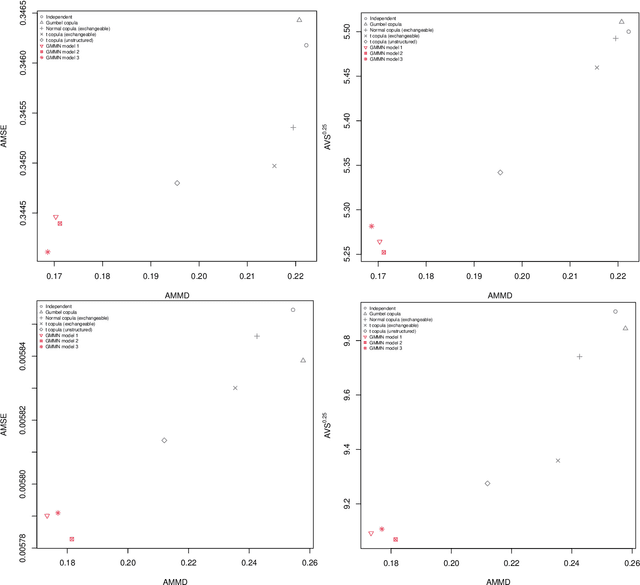
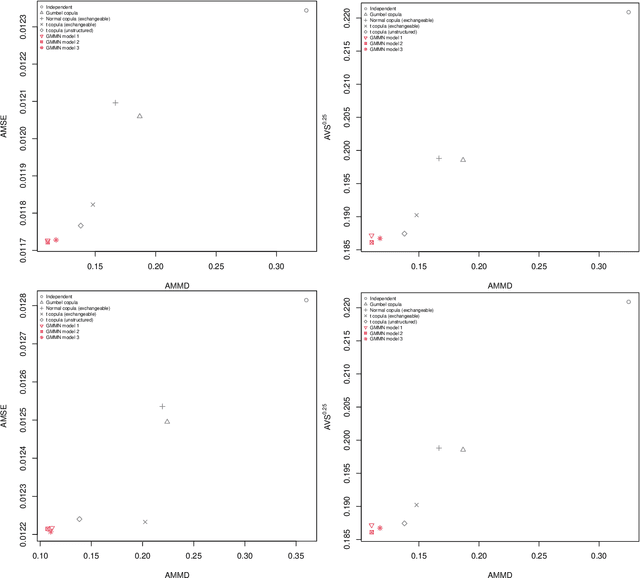
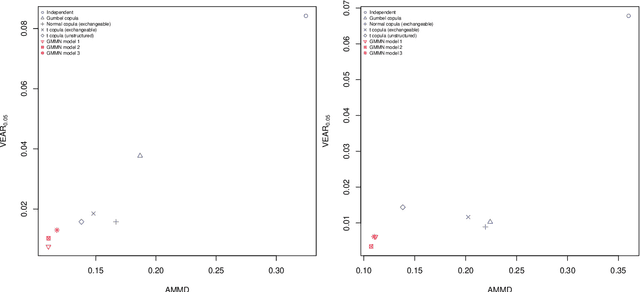
An adaptive bandwidth selection procedure for the mixture kernel in the maximum mean discrepancy (MMD) for fitting generative moment matching networks (GMMNs) is introduced, and its ability to improve the learning of copula random number generators is demonstrated. Based on the relative error of the training loss, the number of kernels is increased during training; additionally, the relative error of the validation loss is used as an early stopping criterion. While training time of such adaptively trained GMMNs (AGMMNs) is similar to that of GMMNs, training performance is increased significantly in comparison to GMMNs, which is assessed and shown based on validation MMD trajectories, samples and validation MMD values. Superiority of AGMMNs over GMMNs, as well as typical parametric copula models, is demonstrated in terms of three applications. First, convergence rates of quasi-random versus pseudo-random samples from high-dimensional copulas are investigated for three functionals of interest and in dimensions as large as 100 for the first time. Second, replicated validation MMDs, as well as Monte Carlo and quasi-Monte Carlo applications based on the expected payoff of a basked call option and the risk measure expected shortfall as functionals are used to demonstrate the improved training of AGMMNs over GMMNs for a copula model fitted to the standardized residuals of the 50 constituents of the S&P 500 index after deGARCHing. Last, both the latter dataset and 50 constituents of the FTSE~100 are used to demonstrate that the improved training of AGMMNs over GMMNs and in comparison to the fitting of classical parametric copula models indeed also translates to an improved model prediction.

Dependence model assessment and selection with DecoupleNets

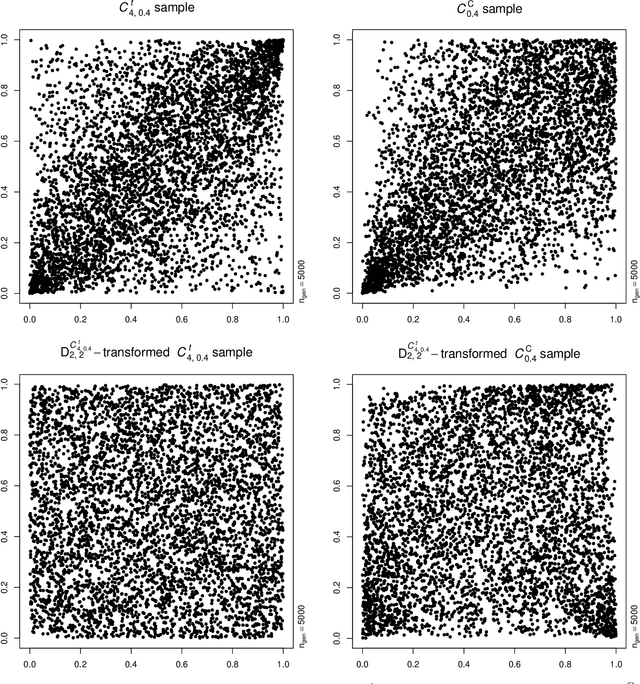
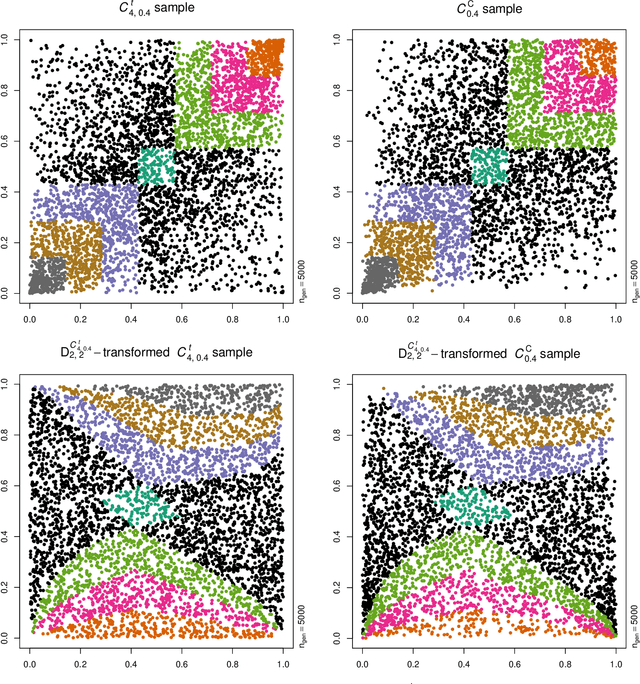
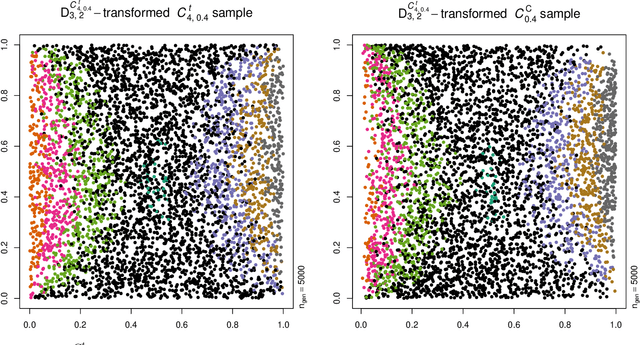
Neural networks are suggested for learning a map from $d$-dimensional samples with any underlying dependence structure to multivariate uniformity in $d'$ dimensions. This map, termed DecoupleNet, is used for dependence model assessment and selection. If the data-generating dependence model was known, and if it was among the few analytically tractable ones, one such transformation for $d'=d$ is Rosenblatt's transform. DecoupleNets only require an available sample and are applicable to $d'<d$, in particular $d'=2$. This allows for simpler model assessment and selection without loss of information, both numerically and, because $d'=2$, graphically. Through simulation studies based on data from various copulas, the feasibility and validity of this novel approach is demonstrated. Applications to real world data illustrate its usefulness for model assessment and selection.

RafterNet: Probabilistic predictions in multi-response regression

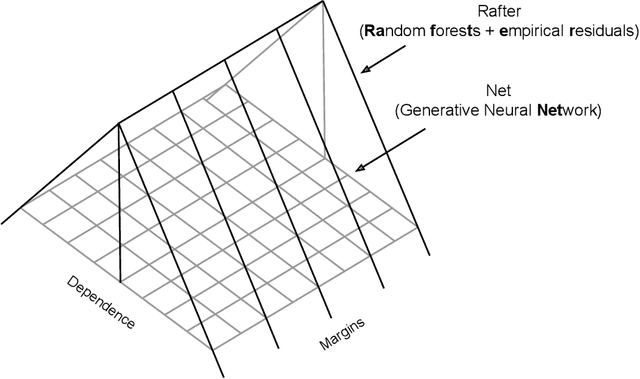
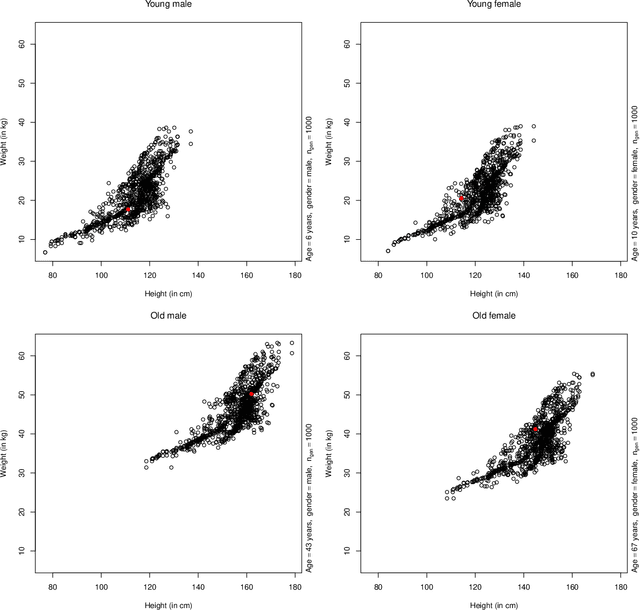
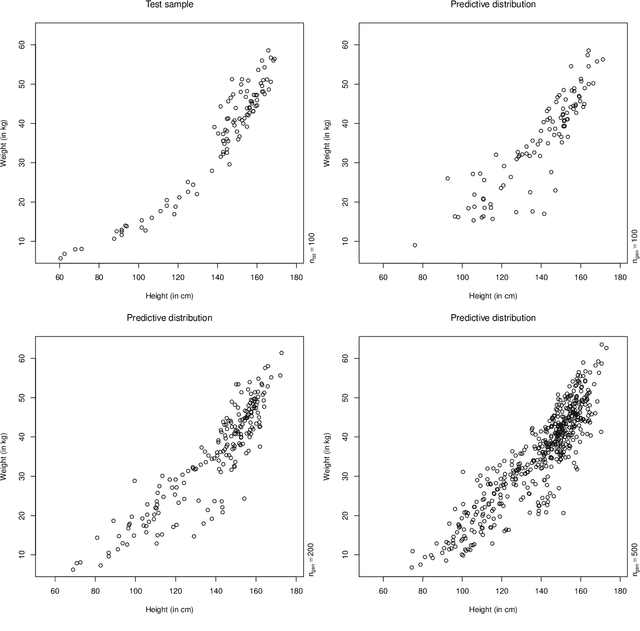
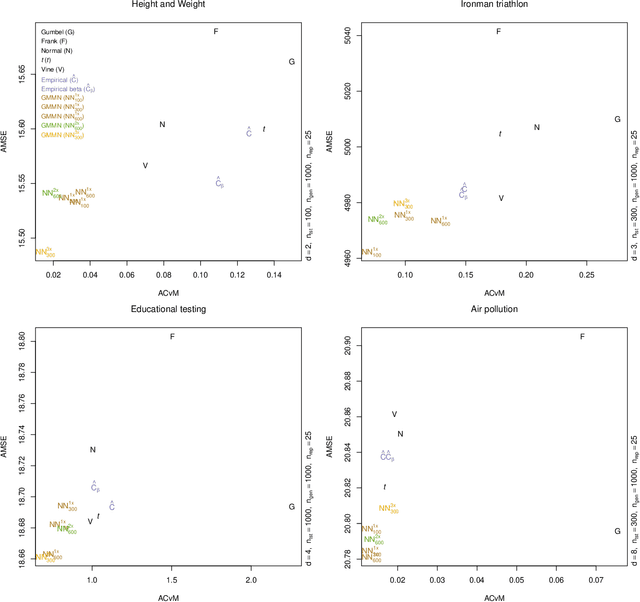
A fully nonparametric approach for making probabilistic predictions in multi-response regression problems is introduced. Random forests are used as marginal models for each response variable and, as novel contribution of the present work, the dependence between the multiple response variables is modeled by a generative neural network. This combined modeling approach of random forests, corresponding empirical marginal residual distributions and a generative neural network is referred to as RafterNet. Multiple datasets serve as examples to demonstrate the flexibility of the approach and its impact for making probabilistic forecasts.

Applications of multivariate quasi-random sampling with neural networks

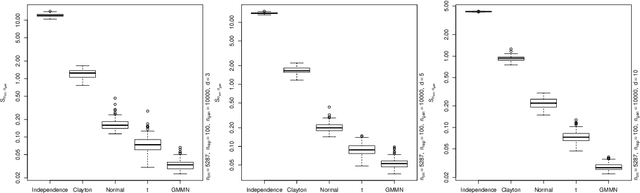
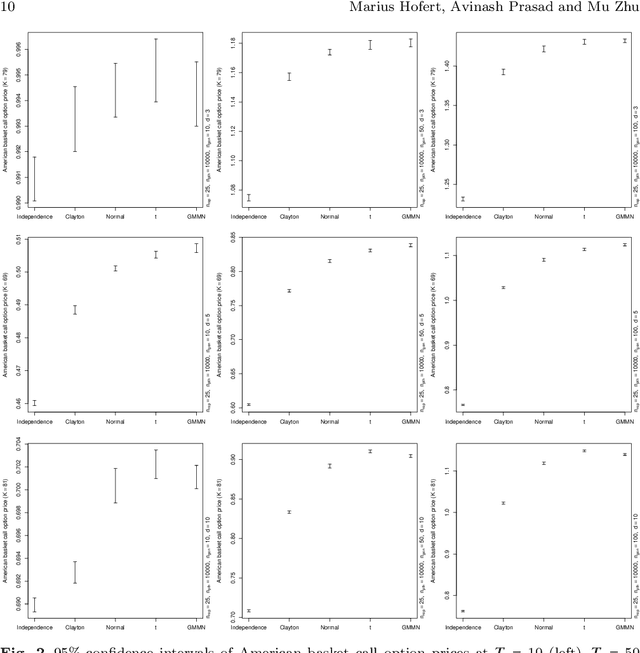
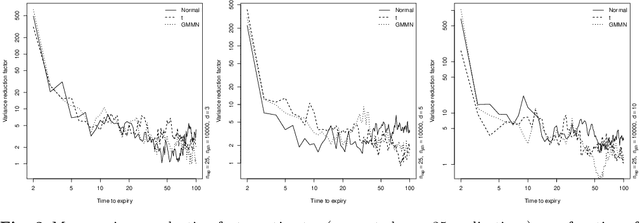
Generative moment matching networks (GMMNs) are suggested for modeling the cross-sectional dependence between stochastic processes. The stochastic processes considered are geometric Brownian motions and ARMA-GARCH models. Geometric Brownian motions lead to an application of pricing American basket call options under dependence and ARMA-GARCH models lead to an application of simulating predictive distributions. In both types of applications the benefit of using GMMNs in comparison to parametric dependence models is highlighted and the fact that GMMNs can produce dependent quasi-random samples with no additional effort is exploited to obtain variance reduction.

Multivariate time-series modeling with generative neural networks

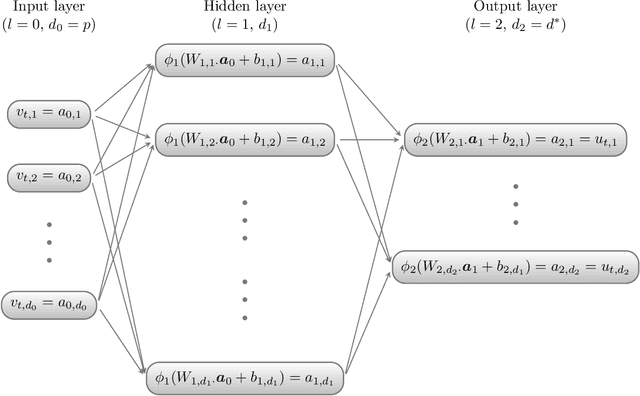
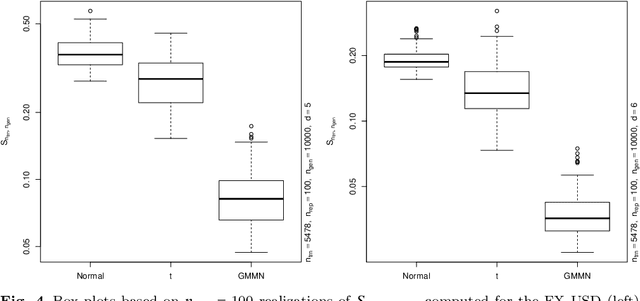
Generative moment matching networks (GMMNs) are introduced as dependence models for the joint innovation distribution of multivariate time series (MTS). Following the popular copula-GARCH approach for modeling dependent MTS data, a framework allowing us to take an alternative GMMN-GARCH approach is presented. First, ARMA-GARCH models are utilized to capture the serial dependence within each univariate marginal time series. Second, if the number of marginal time series is large, principal component analysis (PCA) is used as a dimension-reduction step. Last, the remaining cross-sectional dependence is modeled via a GMMN, our main contribution. GMMNs are highly flexible and easy to simulate from, which is a major advantage over the copula-GARCH approach. Applications involving yield curve modeling and the analysis of foreign exchange rate returns are presented to demonstrate the utility of our approach, especially in terms of producing better empirical predictive distributions and making better probabilistic forecasts. All results are reproducible with the demo GMMN_MTS_paper of the R package gnn.

Quasi-random number generators for multivariate distributions based on generative neural networks

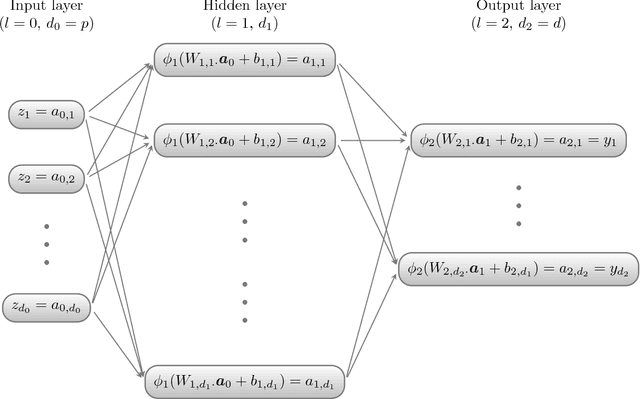
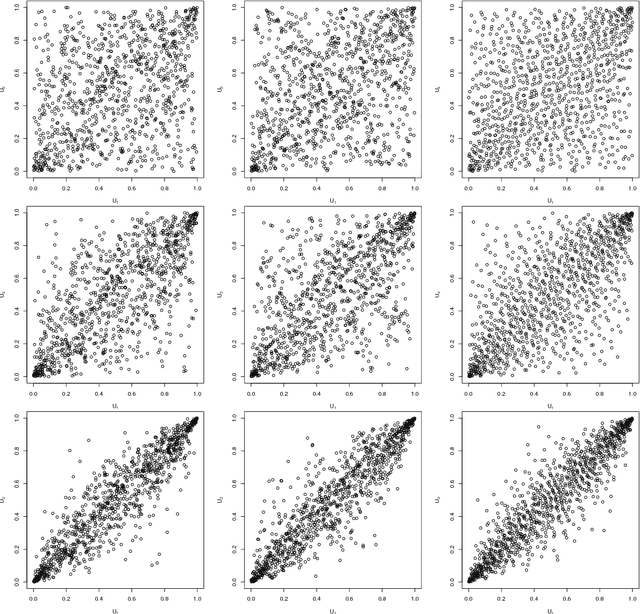
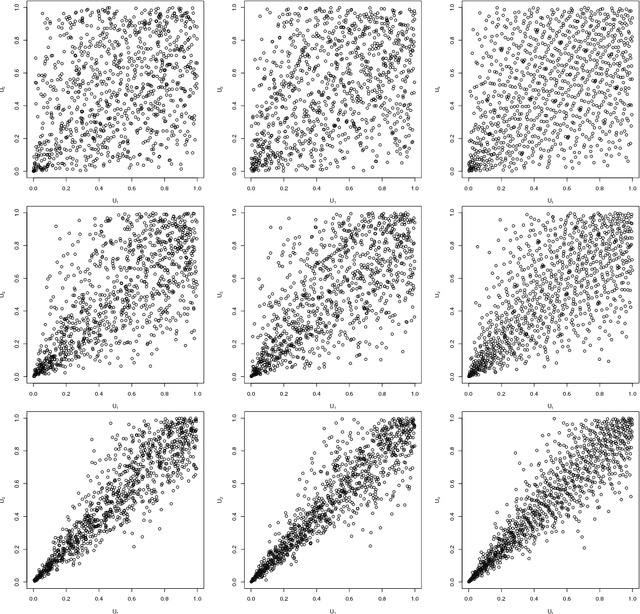
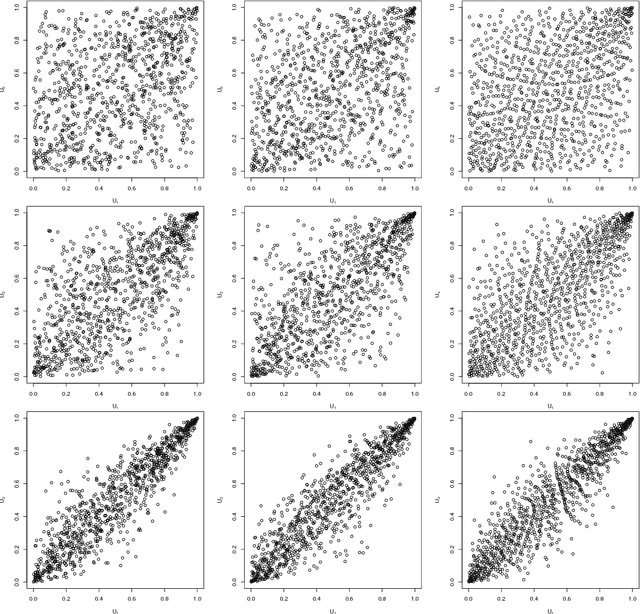
Generative moment matching networks are introduced as quasi-random number generators for multivariate distributions. So far, quasi-random number generators for non-uniform multivariate distributions require a careful design, often need to exploit specific properties of the distribution or quasi-random number sequence under consideration, and are limited to few models. Utilizing generative neural networks, in particular, generative moment matching networks, allows one to construct quasi-random number generators for a much larger variety of multivariate distributions without such restrictions. Once trained, the presented generators only require independent quasi-random numbers as input and are thus fast in generating non-uniform multivariate quasi-random number sequences from the target distribution. Various numerical examples are considered to demonstrate the approach, including applications inspired by risk management practice.