Flexible SE(2) graph neural networks with applications to PDE surrogates

This paper presents a novel approach for constructing graph neural networks equivariant to 2D rotations and translations and leveraging them as PDE surrogates on non-gridded domains. We show that aligning the representations with the principal axis allows us to sidestep many constraints while preserving SE(2) equivariance. By applying our model as a surrogate for fluid flow simulations and conducting thorough benchmarks against non-equivariant models, we demonstrate significant gains in terms of both data efficiency and accuracy.

Ising on the Graph: Task-specific Graph Subsampling via the Ising Model

Reducing a graph while preserving its overall structure is an important problem with many applications. Typically, the reduction approaches either remove edges (sparsification) or merge nodes (coarsening) in an unsupervised way with no specific downstream task in mind. In this paper, we present an approach for subsampling graph structures using an Ising model defined on either the nodes or edges and learning the external magnetic field of the Ising model using a graph neural network. Our approach is task-specific as it can learn how to reduce a graph for a specific downstream task in an end-to-end fashion. The utilized loss function of the task does not even have to be differentiable. We showcase the versatility of our approach on three distinct applications: image segmentation, 3D shape sparsification, and sparse approximate matrix inverse determination.

Carbohydrate NMR chemical shift predictions using E(3) equivariant graph neural networks

Carbohydrates, vital components of biological systems, are well-known for their structural diversity. Nuclear Magnetic Resonance (NMR) spectroscopy plays a crucial role in understanding their intricate molecular arrangements and is essential in assessing and verifying the molecular structure of organic molecules. An important part of this process is to predict the NMR chemical shift from the molecular structure. This work introduces a novel approach that leverages E(3) equivariant graph neural networks to predict carbohydrate NMR spectra. Notably, our model achieves a substantial reduction in mean absolute error, up to threefold, compared to traditional models that rely solely on two-dimensional molecular structure. Even with limited data, the model excels, highlighting its robustness and generalization capabilities. The implications are far-reaching and go beyond an advanced understanding of carbohydrate structures and spectral interpretation. For example, it could accelerate research in pharmaceutical applications, biochemistry, and structural biology, offering a faster and more reliable analysis of molecular structures. Furthermore, our approach is a key step towards a new data-driven era in spectroscopy, potentially influencing spectroscopic techniques beyond NMR.

Variational Elliptical Processes

We present elliptical processes, a family of non-parametric probabilistic models that subsume Gaussian processes and Student's t processes. This generalization includes a range of new heavy-tailed behaviors while retaining computational tractability. Elliptical processes are based on a representation of elliptical distributions as a continuous mixture of Gaussian distributions. We parameterize this mixture distribution as a spline normalizing flow, which we train using variational inference. The proposed form of the variational posterior enables a sparse variational elliptical process applicable to large-scale problems. We highlight advantages compared to Gaussian processes through regression and classification experiments. Elliptical processes can supersede Gaussian processes in several settings, including cases where the likelihood is non-Gaussian or when accurate tail modeling is essential.

Pre-training Transformers for Molecular Property Prediction Using Reaction Prediction

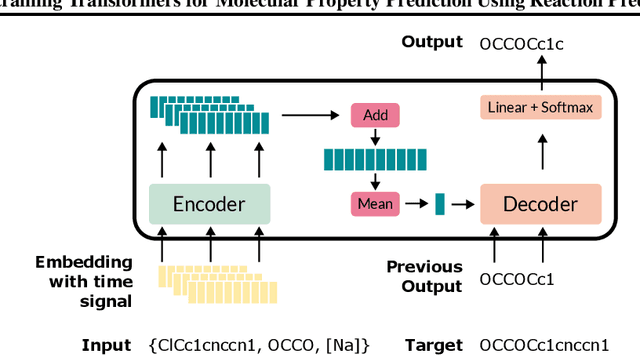
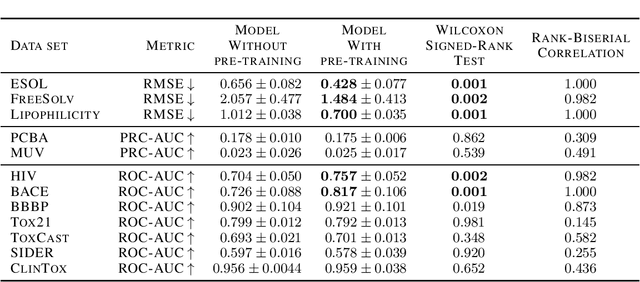
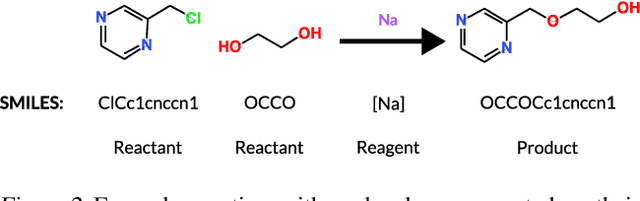
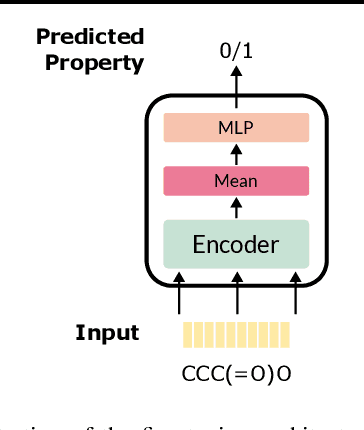
Molecular property prediction is essential in chemistry, especially for drug discovery applications. However, available molecular property data is often limited, encouraging the transfer of information from related data. Transfer learning has had a tremendous impact in fields like Computer Vision and Natural Language Processing signaling for its potential in molecular property prediction. We present a pre-training procedure for molecular representation learning using reaction data and use it to pre-train a SMILES Transformer. We fine-tune and evaluate the pre-trained model on 12 molecular property prediction tasks from MoleculeNet within physical chemistry, biophysics, and physiology and show a statistically significant positive effect on 5 of the 12 tasks compared to a non-pre-trained baseline model.

Graph-based Neural Acceleration for Nonnegative Matrix Factorization

We describe a graph-based neural acceleration technique for nonnegative matrix factorization that builds upon a connection between matrices and bipartite graphs that is well-known in certain fields, e.g., sparse linear algebra, but has not yet been exploited to design graph neural networks for matrix computations. We first consider low-rank factorization more broadly and propose a graph representation of the problem suited for graph neural networks. Then, we focus on the task of nonnegative matrix factorization and propose a graph neural network that interleaves bipartite self-attention layers with updates based on the alternating direction method of multipliers. Our empirical evaluation on synthetic and two real-world datasets shows that we attain substantial acceleration, even though we only train in an unsupervised fashion on smaller synthetic instances.

The Elliptical Processes: a New Family of Flexible Stochastic Processes

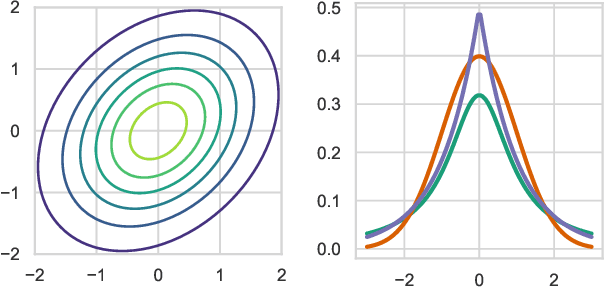
We present the elliptical processes-a new family of stochastic processes that subsumes the Gaussian process and the Student-t process. This generalization retains computational tractability while substantially increasing the range of tail behaviors that can be modeled. We base the elliptical processes on a representation of elliptical distributions as mixtures of Gaussian distributions and derive closed-form expressions for the marginal and conditional distributions. We perform an in-depth study of a particular elliptical process, where the mixture distribution is piecewise constant, and show some of its advantages over the Gaussian process through a number of experiments on robust regression. Looking forward, we believe there are several settings, e.g. when the likelihood is not Gaussian or when accurate tail modeling is critical, where the elliptical processes could become the stochastic processes of choice.

Constructing the Matrix Multilayer Perceptron and its Application to the VAE

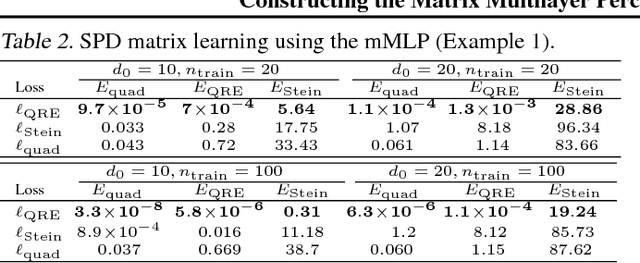
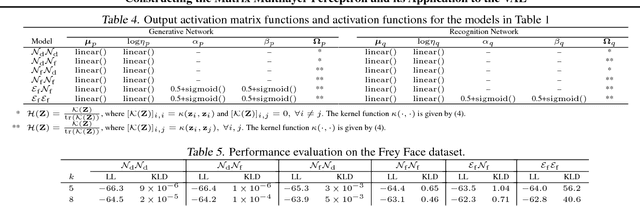
Like most learning algorithms, the multilayer perceptrons (MLP) is designed to learn a vector of parameters from data. However, in certain scenarios we are interested in learning structured parameters (predictions) in the form of symmetric positive definite matrices. Here, we introduce a variant of the MLP, referred to as the matrix MLP, that is specialized at learning symmetric positive definite matrices. We also present an application of the model within the context of the variational autoencoder (VAE). Our formulation of the VAE extends the vanilla formulation to the cases where the recognition and the generative networks can be from the parametric family of distributions with dense covariance matrices. Two specific examples are discussed in more detail: the dense covariance Gaussian and its generalization, the power exponential distribution. Our new developments are illustrated using both synthetic and real data.