The Loss Rank Principle for Model Selection

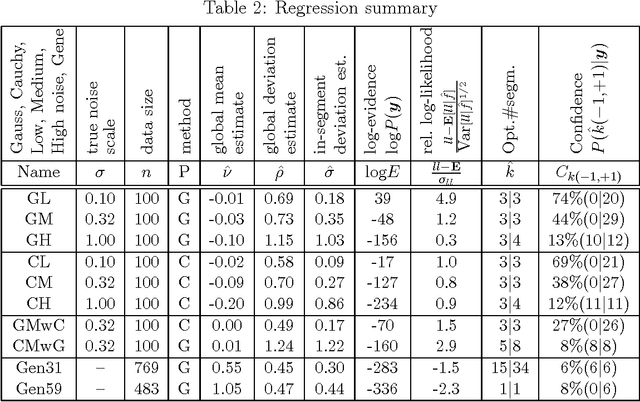
We introduce a new principle for model selection in regression and classification. Many regression models are controlled by some smoothness or flexibility or complexity parameter c, e.g. the number of neighbors to be averaged over in k nearest neighbor (kNN) regression or the polynomial degree in regression with polynomials. Let f_D^c be the (best) regressor of complexity c on data D. A more flexible regressor can fit more data D' well than a more rigid one. If something (here small loss) is easy to achieve it's typically worth less. We define the loss rank of f_D^c as the number of other (fictitious) data D' that are fitted better by f_D'^c than D is fitted by f_D^c. We suggest selecting the model complexity c that has minimal loss rank (LoRP). Unlike most penalized maximum likelihood variants (AIC,BIC,MDL), LoRP only depends on the regression function and loss function. It works without a stochastic noise model, and is directly applicable to any non-parametric regressor, like kNN. In this paper we formalize, discuss, and motivate LoRP, study it for specific regression problems, in particular linear ones, and compare it to other model selection schemes.

Universal Algorithmic Intelligence: A mathematical top->down approach

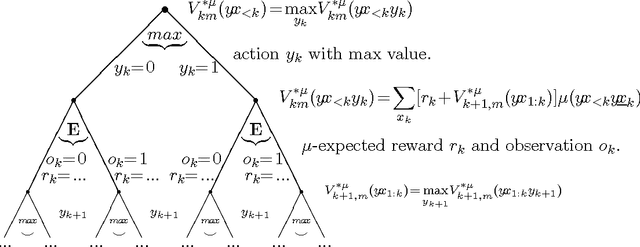
Sequential decision theory formally solves the problem of rational agents in uncertain worlds if the true environmental prior probability distribution is known. Solomonoff's theory of universal induction formally solves the problem of sequence prediction for unknown prior distribution. We combine both ideas and get a parameter-free theory of universal Artificial Intelligence. We give strong arguments that the resulting AIXI model is the most intelligent unbiased agent possible. We outline how the AIXI model can formally solve a number of problem classes, including sequence prediction, strategic games, function minimization, reinforcement and supervised learning. The major drawback of the AIXI model is that it is uncomputable. To overcome this problem, we construct a modified algorithm AIXItl that is still effectively more intelligent than any other time t and length l bounded agent. The computation time of AIXItl is of the order t x 2^l. The discussion includes formal definitions of intelligence order relations, the horizon problem and relations of the AIXI theory to other AI approaches.

Fitness Uniform Optimization

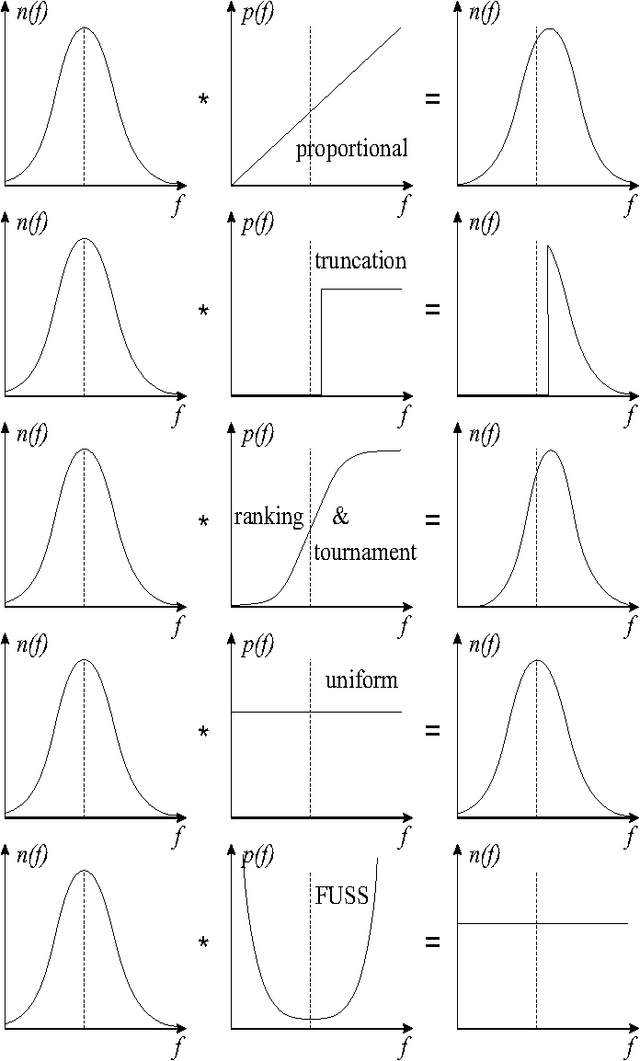
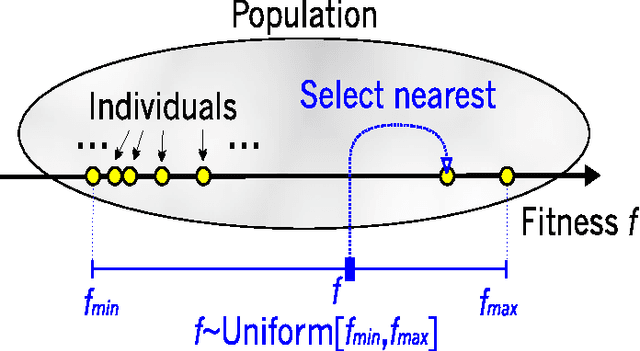
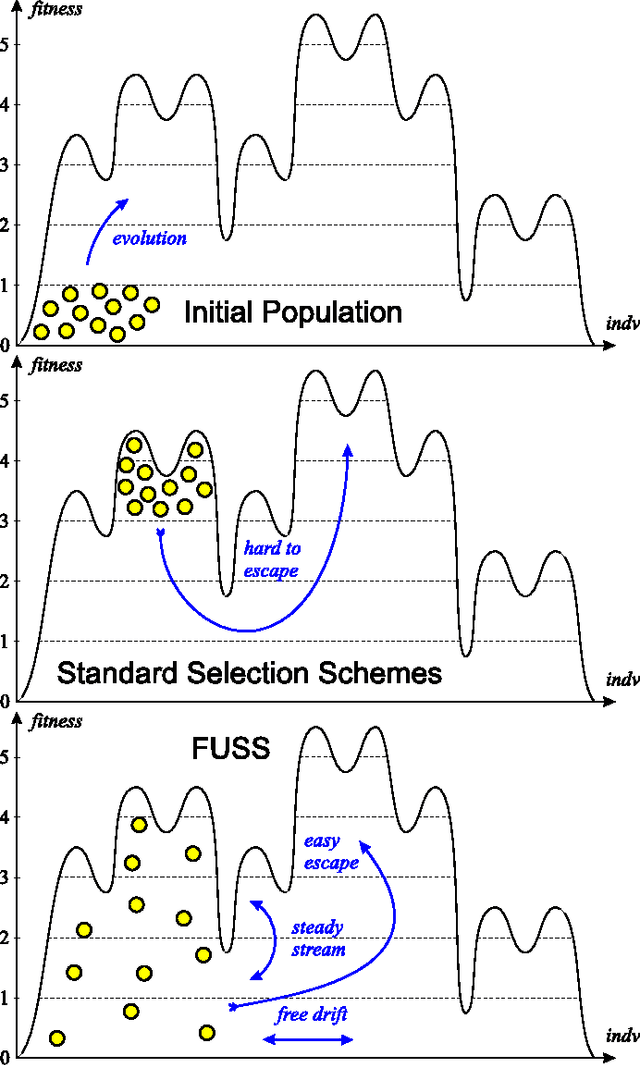
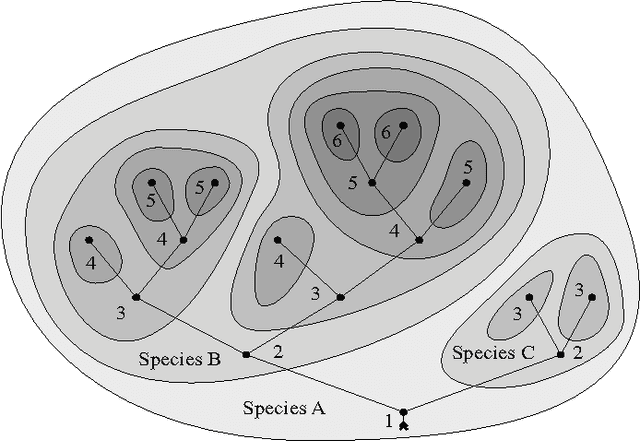
In evolutionary algorithms, the fitness of a population increases with time by mutating and recombining individuals and by a biased selection of more fit individuals. The right selection pressure is critical in ensuring sufficient optimization progress on the one hand and in preserving genetic diversity to be able to escape from local optima on the other hand. Motivated by a universal similarity relation on the individuals, we propose a new selection scheme, which is uniform in the fitness values. It generates selection pressure toward sparsely populated fitness regions, not necessarily toward higher fitness, as is the case for all other selection schemes. We show analytically on a simple example that the new selection scheme can be much more effective than standard selection schemes. We also propose a new deletion scheme which achieves a similar result via deletion and show how such a scheme preserves genetic diversity more effectively than standard approaches. We compare the performance of the new schemes to tournament selection and random deletion on an artificial deceptive problem and a range of NP-hard problems: traveling salesman, set covering and satisfiability.

On Sequence Prediction for Arbitrary Measures

Suppose we are given two probability measures on the set of one-way infinite finite-alphabet sequences and consider the question when one of the measures predicts the other, that is, when conditional probabilities converge (in a certain sense) when one of the measures is chosen to generate the sequence. This question may be considered a refinement of the problem of sequence prediction in its most general formulation: for a given class of probability measures, does there exist a measure which predicts all of the measures in the class? To address this problem, we find some conditions on local absolute continuity which are sufficient for prediction and which generalize several different notions which are known to be sufficient for prediction. We also formulate some open questions to outline a direction for finding the conditions on classes of measures for which prediction is possible.

Bayesian Regression of Piecewise Constant Functions

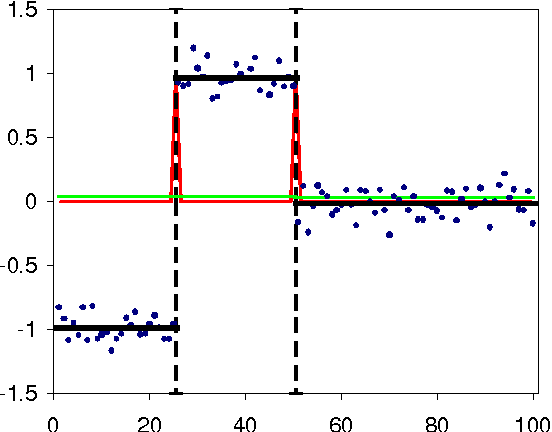
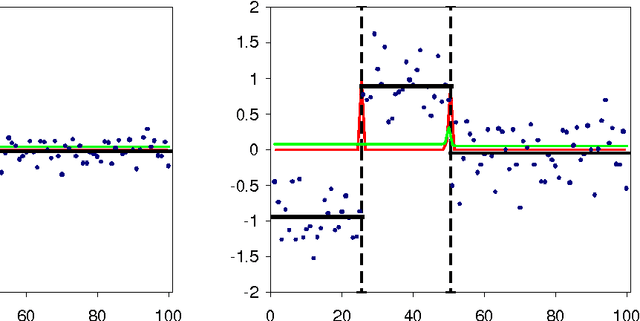
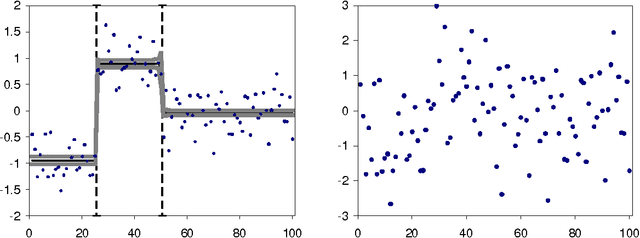
We derive an exact and efficient Bayesian regression algorithm for piecewise constant functions of unknown segment number, boundary location, and levels. It works for any noise and segment level prior, e.g. Cauchy which can handle outliers. We derive simple but good estimates for the in-segment variance. We also propose a Bayesian regression curve as a better way of smoothing data without blurring boundaries. The Bayesian approach also allows straightforward determination of the evidence, break probabilities and error estimates, useful for model selection and significance and robustness studies. We discuss the performance on synthetic and real-world examples. Many possible extensions will be discussed.

General Discounting versus Average Reward

Consider an agent interacting with an environment in cycles. In every interaction cycle the agent is rewarded for its performance. We compare the average reward U from cycle 1 to m (average value) with the future discounted reward V from cycle k to infinity (discounted value). We consider essentially arbitrary (non-geometric) discount sequences and arbitrary reward sequences (non-MDP environments). We show that asymptotically U for m->infinity and V for k->infinity are equal, provided both limits exist. Further, if the effective horizon grows linearly with k or faster, then existence of the limit of U implies that the limit of V exists. Conversely, if the effective horizon grows linearly with k or slower, then existence of the limit of V implies that the limit of U exists.

A Formal Measure of Machine Intelligence

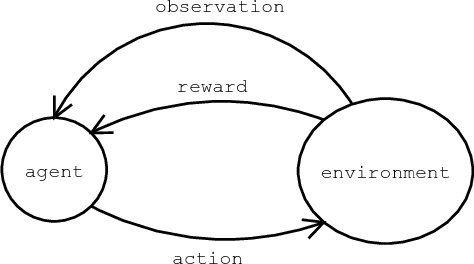
A fundamental problem in artificial intelligence is that nobody really knows what intelligence is. The problem is especially acute when we need to consider artificial systems which are significantly different to humans. In this paper we approach this problem in the following way: We take a number of well known informal definitions of human intelligence that have been given by experts, and extract their essential features. These are then mathematically formalised to produce a general measure of intelligence for arbitrary machines. We believe that this measure formally captures the concept of machine intelligence in the broadest reasonable sense.

On the Foundations of Universal Sequence Prediction

Solomonoff completed the Bayesian framework by providing a rigorous, unique, formal, and universal choice for the model class and the prior. We discuss in breadth how and in which sense universal (non-i.i.d.) sequence prediction solves various (philosophical) problems of traditional Bayesian sequence prediction. We show that Solomonoff's model possesses many desirable properties: Fast convergence and strong bounds, and in contrast to most classical continuous prior densities has no zero p(oste)rior problem, i.e. can confirm universal hypotheses, is reparametrization and regrouping invariant, and avoids the old-evidence and updating problem. It even performs well (actually better) in non-computable environments.

Asymptotic Learnability of Reinforcement Problems with Arbitrary Dependence

We address the problem of reinforcement learning in which observations may exhibit an arbitrary form of stochastic dependence on past observations and actions. The task for an agent is to attain the best possible asymptotic reward where the true generating environment is unknown but belongs to a known countable family of environments. We find some sufficient conditions on the class of environments under which an agent exists which attains the best asymptotic reward for any environment in the class. We analyze how tight these conditions are and how they relate to different probabilistic assumptions known in reinforcement learning and related fields, such as Markov Decision Processes and mixing conditions.

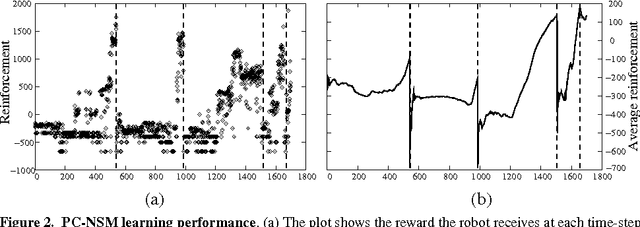
Metric State Space Reinforcement Learning for a Vision-Capable Mobile Robot

We address the problem of autonomously learning controllers for vision-capable mobile robots. We extend McCallum's (1995) Nearest-Sequence Memory algorithm to allow for general metrics over state-action trajectories. We demonstrate the feasibility of our approach by successfully running our algorithm on a real mobile robot. The algorithm is novel and unique in that it (a) explores the environment and learns directly on a mobile robot without using a hand-made computer model as an intermediate step, (b) does not require manual discretization of the sensor input space, (c) works in piecewise continuous perceptual spaces, and (d) copes with partial observability. Together this allows learning from much less experience compared to previous methods.