Feature Markov Decision Processes

General purpose intelligent learning agents cycle through (complex,non-MDP) sequences of observations, actions, and rewards. On the other hand, reinforcement learning is well-developed for small finite state Markov Decision Processes (MDPs). So far it is an art performed by human designers to extract the right state representation out of the bare observations, i.e. to reduce the agent setup to the MDP framework. Before we can think of mechanizing this search for suitable MDPs, we need a formal objective criterion. The main contribution of this article is to develop such a criterion. I also integrate the various parts into one learning algorithm. Extensions to more realistic dynamic Bayesian networks are developed in a companion article.

On the Possibility of Learning in Reactive Environments with Arbitrary Dependence

We address the problem of reinforcement learning in which observations may exhibit an arbitrary form of stochastic dependence on past observations and actions, i.e. environments more general than (PO)MDPs. The task for an agent is to attain the best possible asymptotic reward where the true generating environment is unknown but belongs to a known countable family of environments. We find some sufficient conditions on the class of environments under which an agent exists which attains the best asymptotic reward for any environment in the class. We analyze how tight these conditions are and how they relate to different probabilistic assumptions known in reinforcement learning and related fields, such as Markov Decision Processes and mixing conditions.

Temporal Difference Updating without a Learning Rate

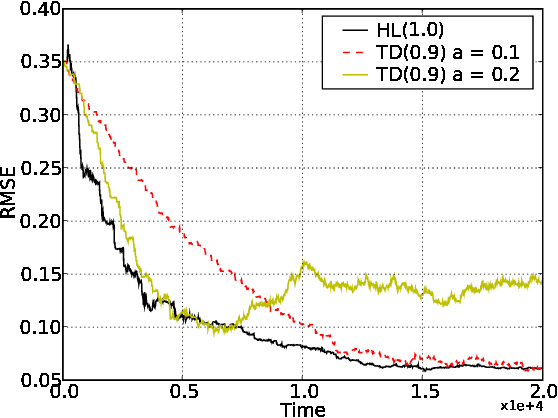
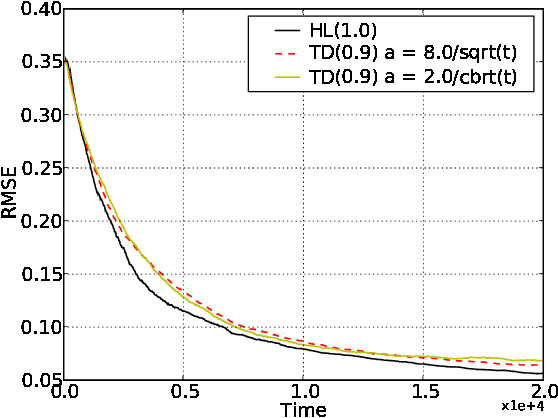
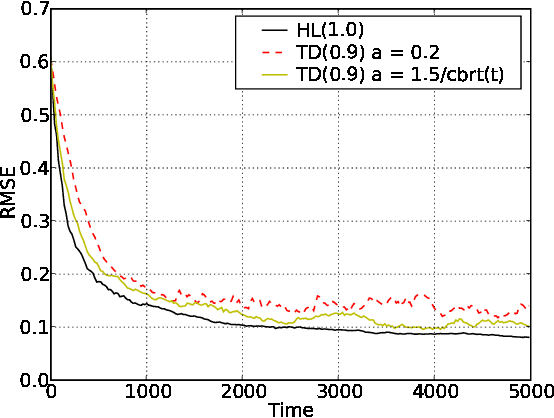
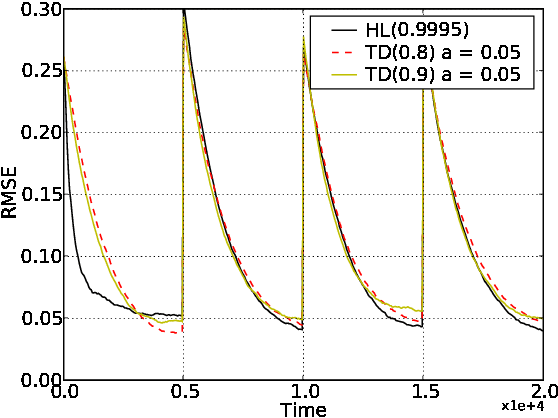
We derive an equation for temporal difference learning from statistical principles. Specifically, we start with the variational principle and then bootstrap to produce an updating rule for discounted state value estimates. The resulting equation is similar to the standard equation for temporal difference learning with eligibility traces, so called TD(lambda), however it lacks the parameter alpha that specifies the learning rate. In the place of this free parameter there is now an equation for the learning rate that is specific to each state transition. We experimentally test this new learning rule against TD(lambda) and find that it offers superior performance in various settings. Finally, we make some preliminary investigations into how to extend our new temporal difference algorithm to reinforcement learning. To do this we combine our update equation with both Watkins' Q(lambda) and Sarsa(lambda) and find that it again offers superior performance without a learning rate parameter.

Predictive Hypothesis Identification

While statistics focusses on hypothesis testing and on estimating (properties of) the true sampling distribution, in machine learning the performance of learning algorithms on future data is the primary issue. In this paper we bridge the gap with a general principle (PHI) that identifies hypotheses with best predictive performance. This includes predictive point and interval estimation, simple and composite hypothesis testing, (mixture) model selection, and others as special cases. For concrete instantiations we will recover well-known methods, variations thereof, and new ones. PHI nicely justifies, reconciles, and blends (a reparametrization invariant variation of) MAP, ML, MDL, and moment estimation. One particular feature of PHI is that it can genuinely deal with nested hypotheses.

Equivalence of Probabilistic Tournament and Polynomial Ranking Selection

Crucial to an Evolutionary Algorithm's performance is its selection scheme. We mathematically investigate the relation between polynomial rank and probabilistic tournament methods which are (respectively) generalisations of the popular linear ranking and tournament selection schemes. We show that every probabilistic tournament is equivalent to a unique polynomial rank scheme. In fact, we derived explicit operators for translating between these two types of selection. Of particular importance is that most linear and most practical quadratic rank schemes are probabilistic tournaments.

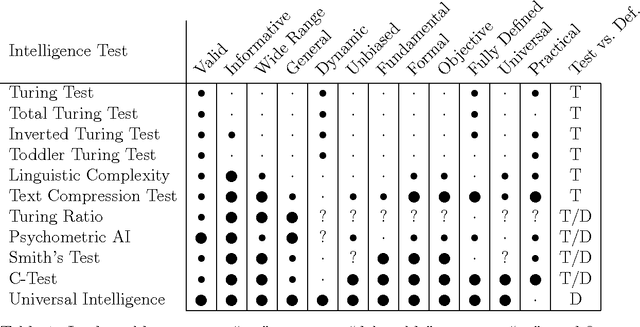
Tests of Machine Intelligence

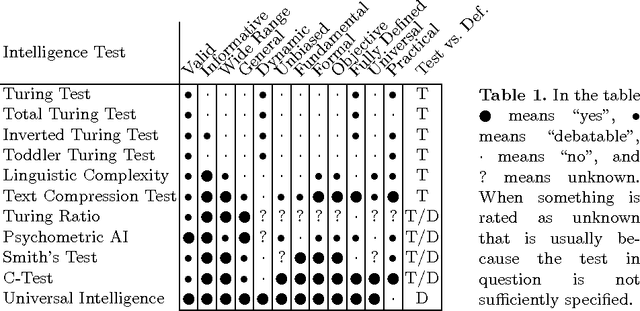
Although the definition and measurement of intelligence is clearly of fundamental importance to the field of artificial intelligence, no general survey of definitions and tests of machine intelligence exists. Indeed few researchers are even aware of alternatives to the Turing test and its many derivatives. In this paper we fill this gap by providing a short survey of the many tests of machine intelligence that have been proposed.

Universal Intelligence: A Definition of Machine Intelligence

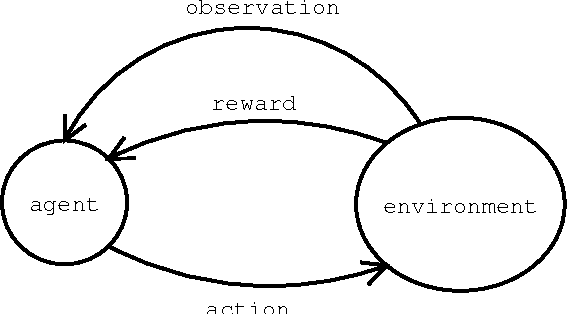
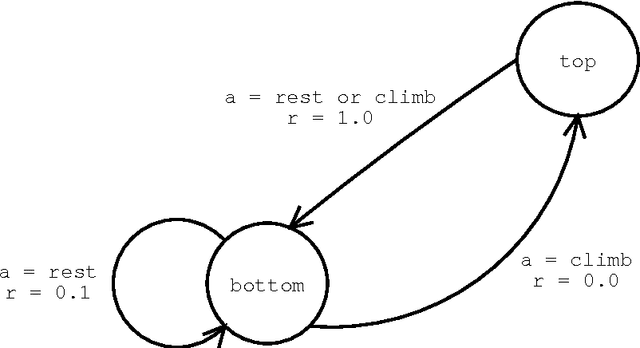
A fundamental problem in artificial intelligence is that nobody really knows what intelligence is. The problem is especially acute when we need to consider artificial systems which are significantly different to humans. In this paper we approach this problem in the following way: We take a number of well known informal definitions of human intelligence that have been given by experts, and extract their essential features. These are then mathematically formalised to produce a general measure of intelligence for arbitrary machines. We believe that this equation formally captures the concept of machine intelligence in the broadest reasonable sense. We then show how this formal definition is related to the theory of universal optimal learning agents. Finally, we survey the many other tests and definitions of intelligence that have been proposed for machines.

On Universal Prediction and Bayesian Confirmation

The Bayesian framework is a well-studied and successful framework for inductive reasoning, which includes hypothesis testing and confirmation, parameter estimation, sequence prediction, classification, and regression. But standard statistical guidelines for choosing the model class and prior are not always available or fail, in particular in complex situations. Solomonoff completed the Bayesian framework by providing a rigorous, unique, formal, and universal choice for the model class and the prior. We discuss in breadth how and in which sense universal (non-i.i.d.) sequence prediction solves various (philosophical) problems of traditional Bayesian sequence prediction. We show that Solomonoff's model possesses many desirable properties: Strong total and weak instantaneous bounds, and in contrast to most classical continuous prior densities has no zero p(oste)rior problem, i.e. can confirm universal hypotheses, is reparametrization and regrouping invariant, and avoids the old-evidence and updating problem. It even performs well (actually better) in non-computable environments.

On Semimeasures Predicting Martin-Loef Random Sequences

Solomonoff's central result on induction is that the posterior of a universal semimeasure M converges rapidly and with probability 1 to the true sequence generating posterior mu, if the latter is computable. Hence, M is eligible as a universal sequence predictor in case of unknown mu. Despite some nearby results and proofs in the literature, the stronger result of convergence for all (Martin-Loef) random sequences remained open. Such a convergence result would be particularly interesting and natural, since randomness can be defined in terms of M itself. We show that there are universal semimeasures M which do not converge for all random sequences, i.e. we give a partial negative answer to the open problem. We also provide a positive answer for some non-universal semimeasures. We define the incomputable measure D as a mixture over all computable measures and the enumerable semimeasure W as a mixture over all enumerable nearly-measures. We show that W converges to D and D to mu on all random sequences. The Hellinger distance measuring closeness of two distributions plays a central role.

A Collection of Definitions of Intelligence

This paper is a survey of a large number of informal definitions of ``intelligence'' that the authors have collected over the years. Naturally, compiling a complete list would be impossible as many definitions of intelligence are buried deep inside articles and books. Nevertheless, the 70-odd definitions presented here are, to the authors' knowledge, the largest and most well referenced collection there is.