V-EfficientNets: Vector-Valued Efficiently Scaled Convolutional Neural Network Models

EfficientNet models are convolutional neural networks optimized for parameter allocation by jointly balancing network width, depth, and resolution. Renowned for their exceptional accuracy, these models have become a standard for image classification tasks across diverse computer vision benchmarks. While traditional neural networks learn correlations between feature channels during training, vector-valued neural networks inherently treat multidimensional data as coherent entities, taking for granted the inter-channel relationships. This paper introduces vector-valued EfficientNets (V-EfficientNets), a novel extension of EfficientNet designed to process arbitrary vector-valued data. The proposed models are evaluated on a medical image classification task, achieving an average accuracy of 99.46% on the ALL-IDB2 dataset for detecting acute lymphoblastic leukemia. V-EfficientNets demonstrate remarkable efficiency, significantly reducing parameters while outperforming state-of-the-art models, including the original EfficientNet. The source code is available at https://github.com/mevalle/v-nets.

Dynamics of Structured Complex-Valued Hopfield Neural Networks

In this paper, we explore the dynamics of structured complex-valued Hopfield neural networks (CvHNNs), which arise when the synaptic weight matrix possesses specific structural properties. We begin by analyzing CvHNNs with a Hermitian synaptic weight matrix and establish the existence of four-cycle dynamics in CvHNNs with skew-Hermitian weight matrices operating synchronously. Furthermore, we introduce two new classes of complex-valued matrices: braided Hermitian and braided skew-Hermitian matrices. We demonstrate that CvHNNs utilizing these matrix types exhibit cycles of length eight when operating in full parallel update mode. Finally, we conduct extensive computational experiments on synchronous CvHNNs, exploring other synaptic weight matrix structures. The findings provide a comprehensive overview of the dynamics of structured CvHNNs, offering insights that may contribute to developing improved associative memory models when integrated with suitable learning rules.

Universal Approximation Theorem for Vector- and Hypercomplex-Valued Neural Networks

The universal approximation theorem states that a neural network with one hidden layer can approximate continuous functions on compact sets with any desired precision. This theorem supports using neural networks for various applications, including regression and classification tasks. Furthermore, it is valid for real-valued neural networks and some hypercomplex-valued neural networks such as complex-, quaternion-, tessarine-, and Clifford-valued neural networks. However, hypercomplex-valued neural networks are a type of vector-valued neural network defined on an algebra with additional algebraic or geometric properties. This paper extends the universal approximation theorem for a wide range of vector-valued neural networks, including hypercomplex-valued models as particular instances. Precisely, we introduce the concept of non-degenerate algebra and state the universal approximation theorem for neural networks defined on such algebras.

Training Single-Layer Morphological Perceptron Using Convex-Concave Programming

This paper concerns the training of a single-layer morphological perceptron using disciplined convex-concave programming (DCCP). We introduce an algorithm referred to as K-DDCCP, which combines the existing single-layer morphological perceptron (SLMP) model proposed by Ritter and Urcid with the weighted disciplined convex-concave programming (WDCCP) algorithm by Charisopoulos and Maragos. The proposed training algorithm leverages the disciplined convex-concave procedure (DCCP) and formulates a non-convex optimization problem for binary classification. To tackle this problem, the constraints are expressed as differences of convex functions, enabling the application of the DCCP package. The experimental results confirm the effectiveness of the K-DDCCP algorithm in solving binary classification problems. Overall, this work contributes to the field of morphological neural networks by proposing an algorithm that extends the capabilities of the SLMP model.

Dual Quaternion Rotational and Translational Equivariance in 3D Rigid Motion Modelling

Objects' rigid motions in 3D space are described by rotations and translations of a highly-correlated set of points, each with associated $x,y,z$ coordinates that real-valued networks consider as separate entities, losing information. Previous works exploit quaternion algebra and their ability to model rotations in 3D space. However, these algebras do not properly encode translations, leading to sub-optimal performance in 3D learning tasks. To overcome these limitations, we employ a dual quaternion representation of rigid motions in the 3D space that jointly describes rotations and translations of point sets, processing each of the points as a single entity. Our approach is translation and rotation equivariant, so it does not suffer from shifts in the data and better learns object trajectories, as we validate in the experimental evaluations. Models endowed with this formulation outperform previous approaches in a human pose forecasting application, attesting to the effectiveness of the proposed dual quaternion formulation for rigid motions in 3D space.

Understanding Vector-Valued Neural Networks and Their Relationship with Real and Hypercomplex-Valued Neural Networks

Despite the many successful applications of deep learning models for multidimensional signal and image processing, most traditional neural networks process data represented by (multidimensional) arrays of real numbers. The intercorrelation between feature channels is usually expected to be learned from the training data, requiring numerous parameters and careful training. In contrast, vector-valued neural networks are conceived to process arrays of vectors and naturally consider the intercorrelation between feature channels. Consequently, they usually have fewer parameters and often undergo more robust training than traditional neural networks. This paper aims to present a broad framework for vector-valued neural networks, referred to as V-nets. In this context, hypercomplex-valued neural networks are regarded as vector-valued models with additional algebraic properties. Furthermore, this paper explains the relationship between vector-valued and traditional neural networks. Precisely, a vector-valued neural network can be obtained by placing restrictions on a real-valued model to consider the intercorrelation between feature channels. Finally, we show how V-nets, including hypercomplex-valued neural networks, can be implemented in current deep-learning libraries as real-valued networks.

Shortest Length Total Orders Do Not Minimize Irregularity in Vector-Valued Mathematical Morphology

Mathematical morphology is a theory concerned with non-linear operators for image processing and analysis. The underlying framework for mathematical morphology is a partially ordered set with well-defined supremum and infimum operations. Because vectors can be ordered in many ways, finding appropriate ordering schemes is a major challenge in mathematical morphology for vector-valued images, such as color and hyperspectral images. In this context, the irregularity issue plays a key role in designing effective morphological operators. Briefly, the irregularity follows from a disparity between the ordering scheme and a metric in the value set. Determining an ordering scheme using a metric provide reasonable approaches to vector-valued mathematical morphology. Because total orderings correspond to paths on the value space, one attempt to reduce the irregularity of morphological operators would be defining a total order based on the shortest length path. However, this paper shows that the total ordering associated with the shortest length path does not necessarily imply minimizing the irregularity.

Extending the Universal Approximation Theorem for a Broad Class of Hypercomplex-Valued Neural Networks

The universal approximation theorem asserts that a single hidden layer neural network approximates continuous functions with any desired precision on compact sets. As an existential result, the universal approximation theorem supports the use of neural networks for various applications, including regression and classification tasks. The universal approximation theorem is not limited to real-valued neural networks but also holds for complex, quaternion, tessarines, and Clifford-valued neural networks. This paper extends the universal approximation theorem for a broad class of hypercomplex-valued neural networks. Precisely, we first introduce the concept of non-degenerate hypercomplex algebra. Complex numbers, quaternions, and tessarines are examples of non-degenerate hypercomplex algebras. Then, we state the universal approximation theorem for hypercomplex-valued neural networks defined on a non-degenerate algebra.

Acute Lymphoblastic Leukemia Detection Using Hypercomplex-Valued Convolutional Neural Networks

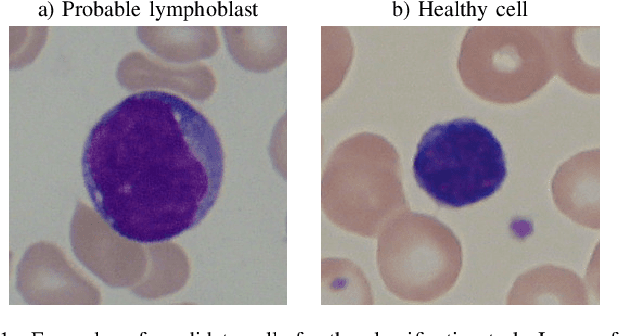
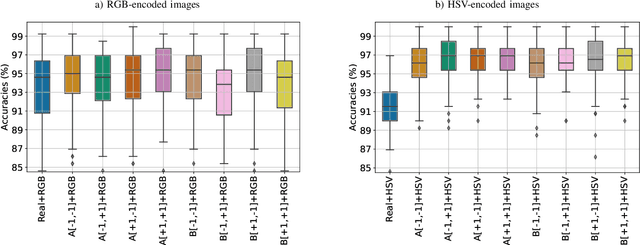
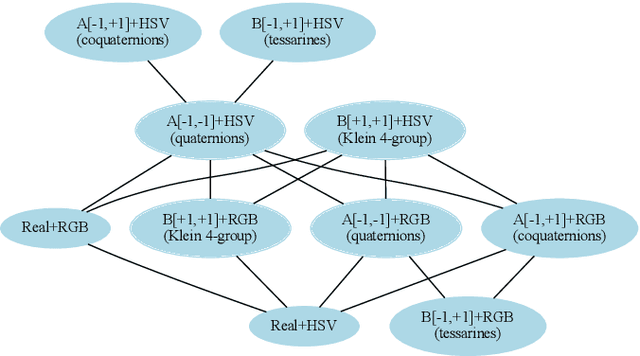
This paper features convolutional neural networks defined on hypercomplex algebras applied to classify lymphocytes in blood smear digital microscopic images. Such classification is helpful for the diagnosis of acute lymphoblast leukemia (ALL), a type of blood cancer. We perform the classification task using eight hypercomplex-valued convolutional neural networks (HvCNNs) along with real-valued convolutional networks. Our results show that HvCNNs perform better than the real-valued model, showcasing higher accuracy with a much smaller number of parameters. Moreover, we found that HvCNNs based on Clifford algebras processing HSV-encoded images attained the highest observed accuracies. Precisely, our HvCNN yielded an average accuracy rate of 96.6% using the ALL-IDB2 dataset with a 50% train-test split, a value extremely close to the state-of-the-art models but using a much simpler architecture with significantly fewer parameters.

Quaternion-Valued Convolutional Neural Network Applied for Acute Lymphoblastic Leukemia Diagnosis

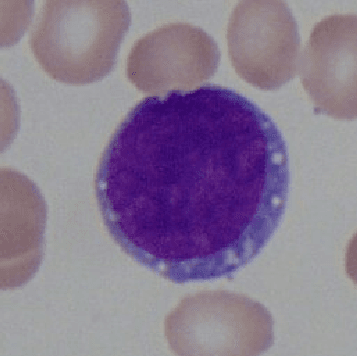
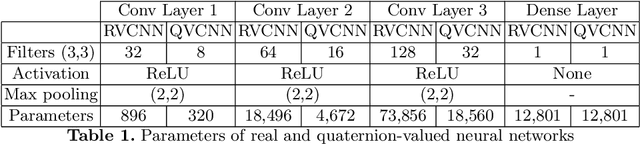
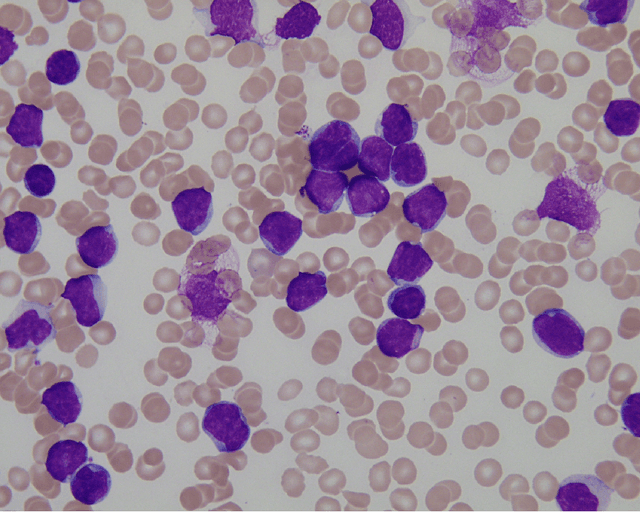
The field of neural networks has seen significant advances in recent years with the development of deep and convolutional neural networks. Although many of the current works address real-valued models, recent studies reveal that neural networks with hypercomplex-valued parameters can better capture, generalize, and represent the complexity of multidimensional data. This paper explores the quaternion-valued convolutional neural network application for a pattern recognition task from medicine, namely, the diagnosis of acute lymphoblastic leukemia. Precisely, we compare the performance of real-valued and quaternion-valued convolutional neural networks to classify lymphoblasts from the peripheral blood smear microscopic images. The quaternion-valued convolutional neural network achieved better or similar performance than its corresponding real-valued network but using only 34% of its parameters. This result confirms that quaternion algebra allows capturing and extracting information from a color image with fewer parameters.