Distance-based classifier by data transformation for high-dimension, strongly spiked eigenvalue models

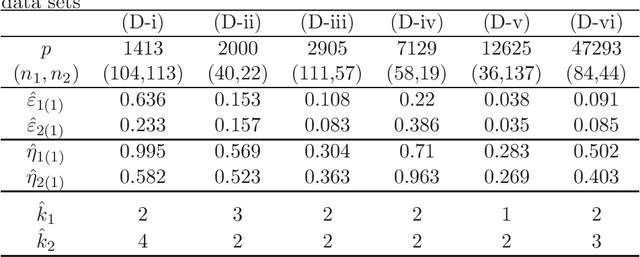
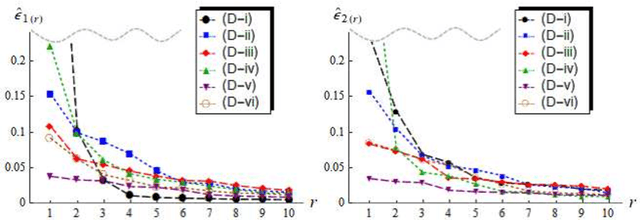
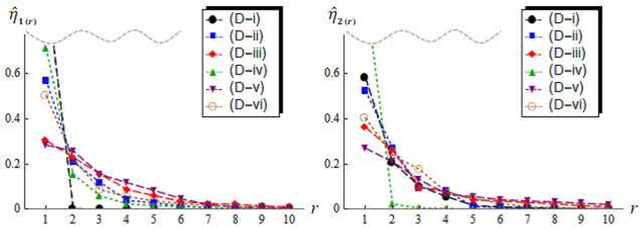
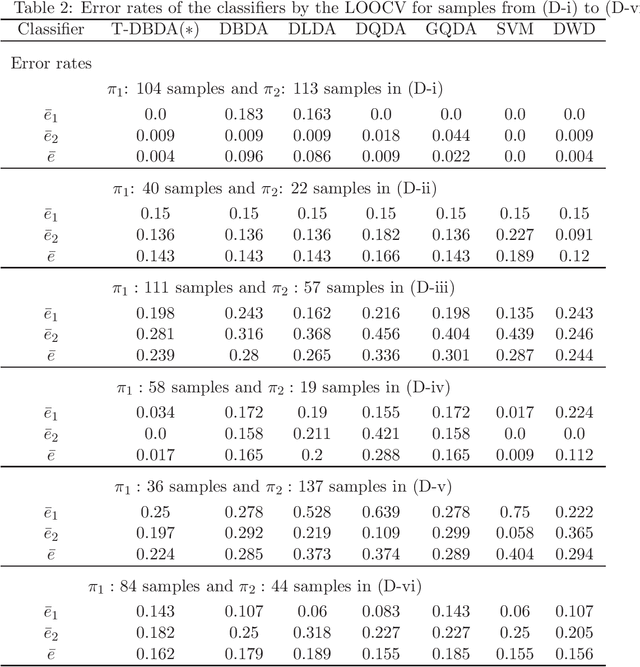
We consider classifiers for high-dimensional data under the strongly spiked eigenvalue (SSE) model. We first show that high-dimensional data often have the SSE model. We consider a distance-based classifier using eigenstructures for the SSE model. We apply the noise reduction methodology to estimation of the eigenvalues and eigenvectors in the SSE model. We create a new distance-based classifier by transforming data from the SSE model to the non-SSE model. We give simulation studies and discuss the performance of the new classifier. Finally, we demonstrate the new classifier by using microarray data sets.

Support vector machine and its bias correction in high-dimension, low-sample-size settings

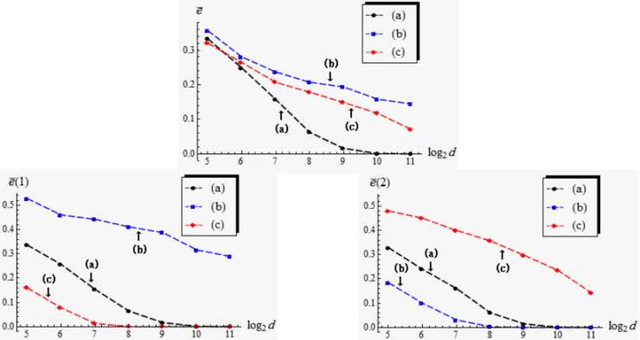
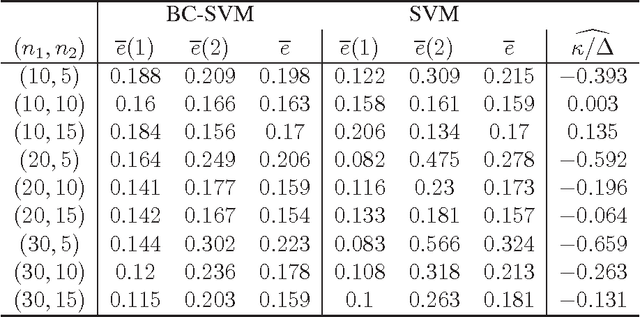
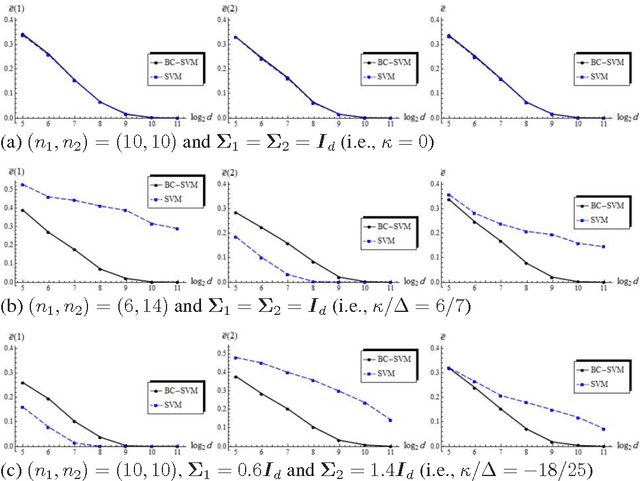
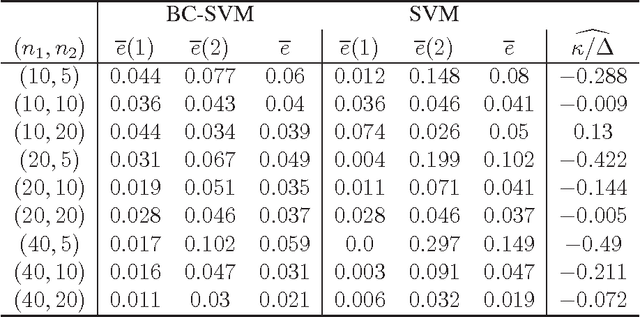
In this paper, we consider asymptotic properties of the support vector machine (SVM) in high-dimension, low-sample-size (HDLSS) settings. We show that the hard-margin linear SVM holds a consistency property in which misclassification rates tend to zero as the dimension goes to infinity under certain severe conditions. We show that the SVM is very biased in HDLSS settings and its performance is affected by the bias directly. In order to overcome such difficulties, we propose a bias-corrected SVM (BC-SVM). We show that the BC-SVM gives preferable performances in HDLSS settings. We also discuss the SVMs in multiclass HDLSS settings. Finally, we check the performance of the classifiers in actual data analyses.

High-dimensional quadratic classifiers in non-sparse settings

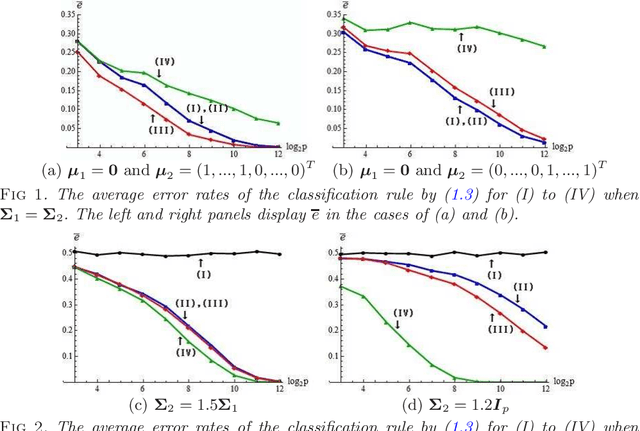
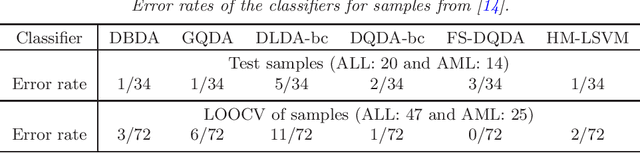
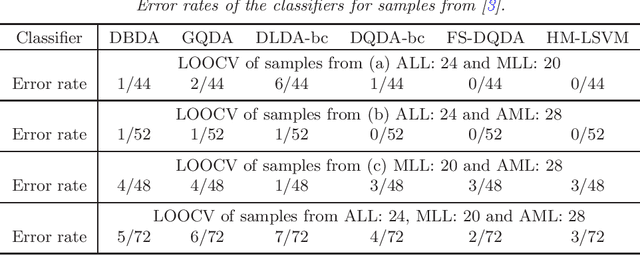
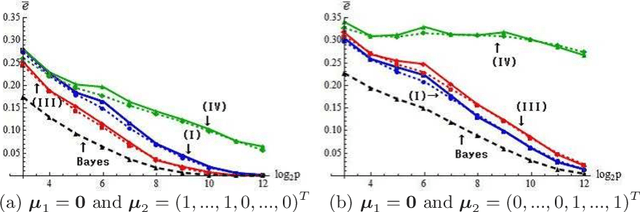
We consider high-dimensional quadratic classifiers in non-sparse settings. The target of classification rules is not Bayes error rates in the context. The classifier based on the Mahalanobis distance does not always give a preferable performance even if the populations are normal distributions having known covariance matrices. The quadratic classifiers proposed in this paper draw information about heterogeneity effectively through both the differences of expanding mean vectors and covariance matrices. We show that they hold a consistency property in which misclassification rates tend to zero as the dimension goes to infinity under non-sparse settings. We verify that they are asymptotically distributed as a normal distribution under certain conditions. We also propose a quadratic classifier after feature selection by using both the differences of mean vectors and covariance matrices. Finally, we discuss performances of the classifiers in actual data analyses. The proposed classifiers achieve highly accurate classification with very low computational costs.