Majid Janzamin
UC Irvine
High-Dimensional Covariance Decomposition into Sparse Markov and Independence Domains
Jun 27, 2012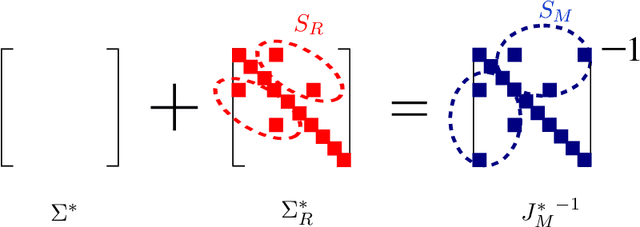
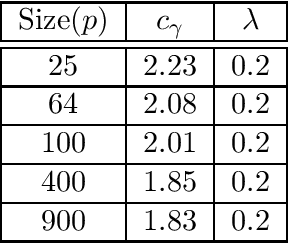
Abstract:In this paper, we present a novel framework incorporating a combination of sparse models in different domains. We posit the observed data as generated from a linear combination of a sparse Gaussian Markov model (with a sparse precision matrix) and a sparse Gaussian independence model (with a sparse covariance matrix). We provide efficient methods for decomposition of the data into two domains, \viz Markov and independence domains. We characterize a set of sufficient conditions for identifiability and model consistency. Our decomposition method is based on a simple modification of the popular $\ell_1$-penalized maximum-likelihood estimator ($\ell_1$-MLE). We establish that our estimator is consistent in both the domains, i.e., it successfully recovers the supports of both Markov and independence models, when the number of samples $n$ scales as $n = \Omega(d^2 \log p)$, where $p$ is the number of variables and $d$ is the maximum node degree in the Markov model. Our conditions for recovery are comparable to those of $\ell_1$-MLE for consistent estimation of a sparse Markov model, and thus, we guarantee successful high-dimensional estimation of a richer class of models under comparable conditions. Our experiments validate these results and also demonstrate that our models have better inference accuracy under simple algorithms such as loopy belief propagation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge