GLAMP: An Approximate Message Passing Framework for Transfer Learning with Applications to Lasso-based Estimators

Approximate Message Passing (AMP) algorithms enable precise characterization of certain classes of random objects in the high-dimensional limit, and have found widespread applications in fields such as statistics, deep learning, genetics, and communications. However, existing AMP frameworks cannot simultaneously handle matrix-valued iterates and non-separable denoising functions. This limitation prevents them from precisely characterizing estimators that draw information from multiple data sources with distribution shifts. In this work, we introduce Generalized Long Approximate Message Passing (GLAMP), a novel extension of AMP that addresses this limitation. We rigorously prove state evolution for GLAMP. GLAMP significantly broadens the scope of AMP, enabling the analysis of transfer learning estimators that were previously out of reach. We demonstrate the utility of GLAMP by precisely characterizing the risk of three Lasso-based transfer learning estimators: the Stacked Lasso, the Model Averaging Estimator, and the Second Step Estimator. We also demonstrate the remarkable finite sample accuracy of our theory via extensive simulations.

Learning and Optimization with Seasonal Patterns

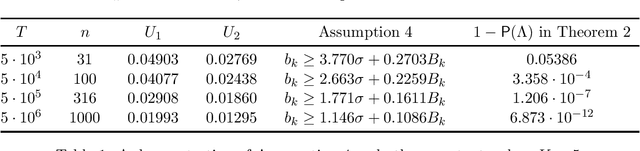
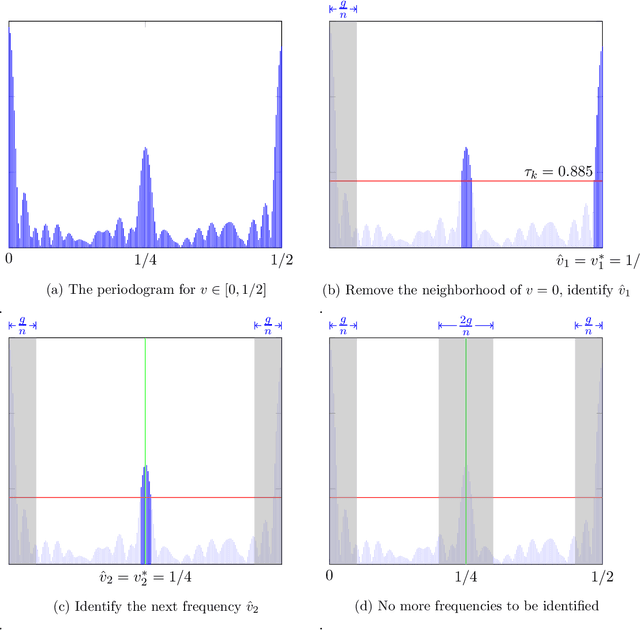
Seasonality is a common form of non-stationary patterns in the business world. We study a decision maker who tries to learn the optimal decision over time when the environment is unknown and evolving with seasonality. We consider a multi-armed bandit (MAB) framework where the mean rewards are periodic. The unknown periods of the arms can be different and scale with the length of the horizon $T$ polynomially. We propose a two-staged policy that combines Fourier analysis with a confidence-bound based learning procedure to learn the periods and minimize the regret. In stage one, the policy is able to correctly estimate the periods of all arms with high probability. In stage two, the policy explores mean rewards of arms in each phase using the periods estimated in stage one and exploits the optimal arm in the long run. We show that our policy achieves the rate of regret $\tilde{O}(\sqrt{T\sum_{k=1}^K T_k})$, where $K$ is the number of arms and $T_k$ is the period of arm $k$. It matches the optimal rate of regret of the classic MAB problem $O(\sqrt{TK})$ if we regard each phase of an arm as a separate arm.