Geometric Structural Knowledge Graph Foundation Model

Structural knowledge graph foundation models aim to generalize reasoning to completely new graphs with unseen entities and relations. A key limitation of existing approaches like Ultra is their reliance on a single relational transformation (e.g., element-wise multiplication) in message passing, which can constrain expressiveness and fail to capture diverse relational and structural patterns exhibited on diverse graphs. In this paper, we propose Gamma, a novel foundation model that introduces multi-head geometric attention to knowledge graph reasoning. Gamma replaces the single relational transformation with multiple parallel ones, including real, complex, split-complex, and dual number based transformations, each designed to model different relational structures. A relational conditioned attention fusion mechanism then adaptively fuses them at link level via a lightweight gating with entropy regularization, allowing the model to robustly emphasize the most appropriate relational bias for each triple pattern. We present a full formalization of these algebraic message functions and discuss how their combination increases expressiveness beyond any single space. Comprehensive experiments on 56 diverse knowledge graphs demonstrate that Gamma consistently outperforms Ultra in zero-shot inductive link prediction, with a 5.5% improvement in mean reciprocal rank on the inductive benchmarks and a 4.4% improvement across all benchmarks, highlighting benefits from complementary geometric representations.

Choosing the number of factors in factor analysis with incomplete data via a hierarchical Bayesian information criterion

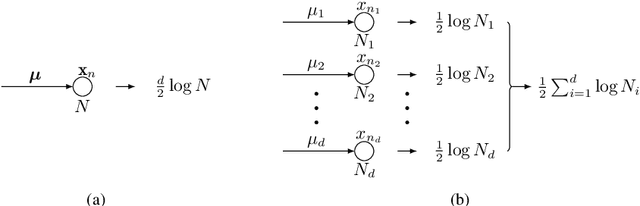
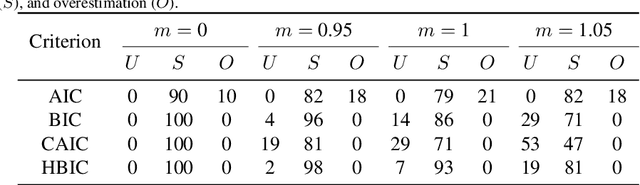
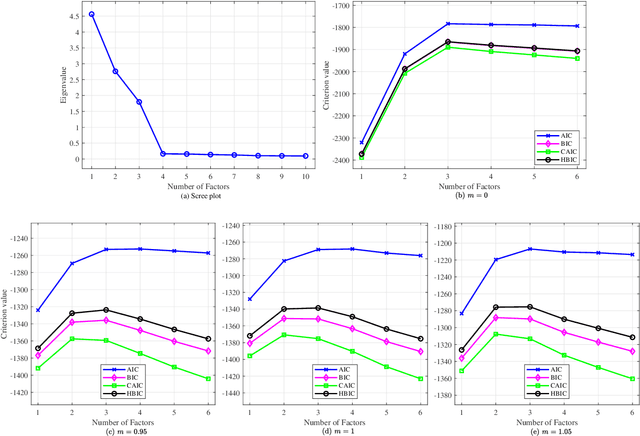
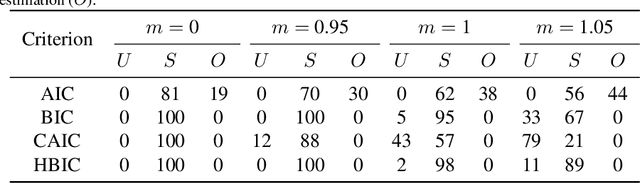
The Bayesian information criterion (BIC), defined as the observed data log likelihood minus a penalty term based on the sample size $N$, is a popular model selection criterion for factor analysis with complete data. This definition has also been suggested for incomplete data. However, the penalty term based on the `complete' sample size $N$ is the same no matter whether in a complete or incomplete data case. For incomplete data, there are often only $N_i<N$ observations for variable $i$, which means that using the `complete' sample size $N$ implausibly ignores the amounts of missing information inherent in incomplete data. Given this observation, a novel criterion called hierarchical BIC (HBIC) for factor analysis with incomplete data is proposed. The novelty is that it only uses the actual amounts of observed information, namely $N_i$'s, in the penalty term. Theoretically, it is shown that HBIC is a large sample approximation of variational Bayesian (VB) lower bound, and BIC is a further approximation of HBIC, which means that HBIC shares the theoretical consistency of BIC. Experiments on synthetic and real data sets are conducted to access the finite sample performance of HBIC, BIC, and related criteria with various missing rates. The results show that HBIC and BIC perform similarly when the missing rate is small, but HBIC is more accurate when the missing rate is not small.