When can in-context learning generalize out of task distribution?

In-context learning (ICL) is a remarkable capability of pretrained transformers that allows models to generalize to unseen tasks after seeing only a few examples. We investigate empirically the conditions necessary on the pretraining distribution for ICL to emerge and generalize \emph{out-of-distribution}. Previous work has focused on the number of distinct tasks necessary in the pretraining dataset. Here, we use a different notion of task diversity to study the emergence of ICL in transformers trained on linear functions. We find that as task diversity increases, transformers undergo a transition from a specialized solution, which exhibits ICL only within the pretraining task distribution, to a solution which generalizes out of distribution to the entire task space. We also investigate the nature of the solutions learned by the transformer on both sides of the transition, and observe similar transitions in nonlinear regression problems. We construct a phase diagram to characterize how our concept of task diversity interacts with the number of pretraining tasks. In addition, we explore how factors such as the depth of the model and the dimensionality of the regression problem influence the transition.

Learning Continuous Chaotic Attractors with a Reservoir Computer

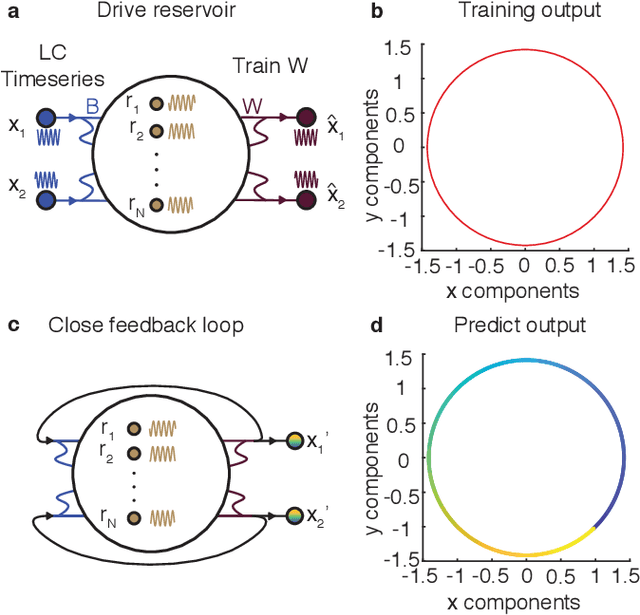
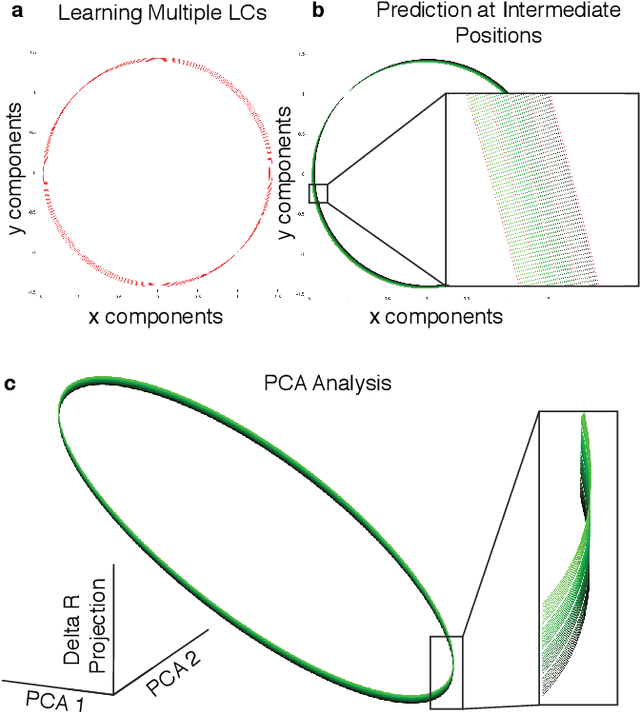
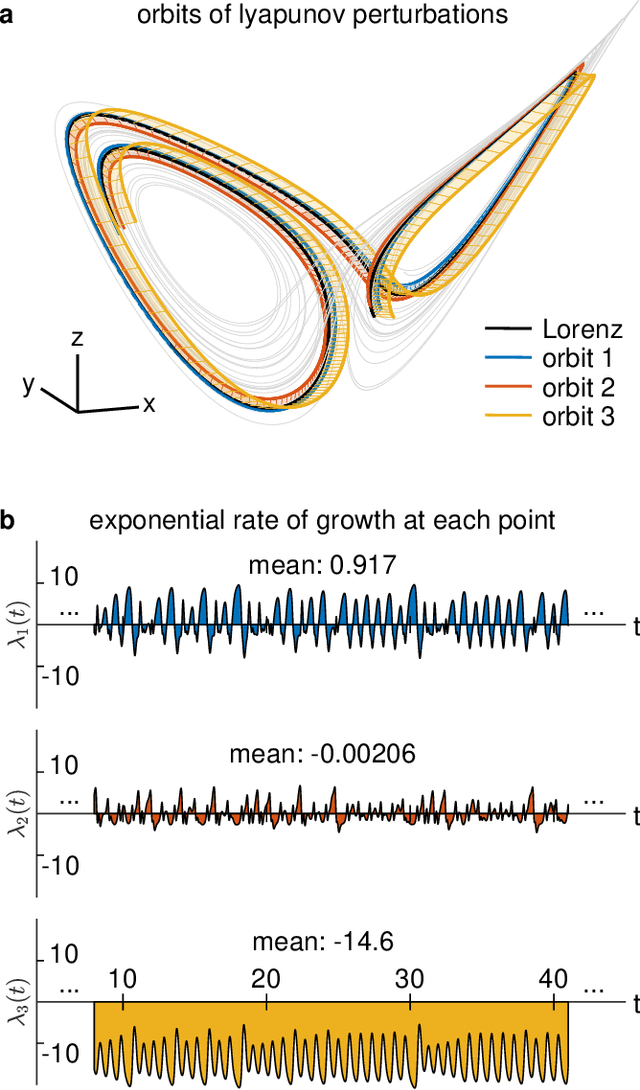
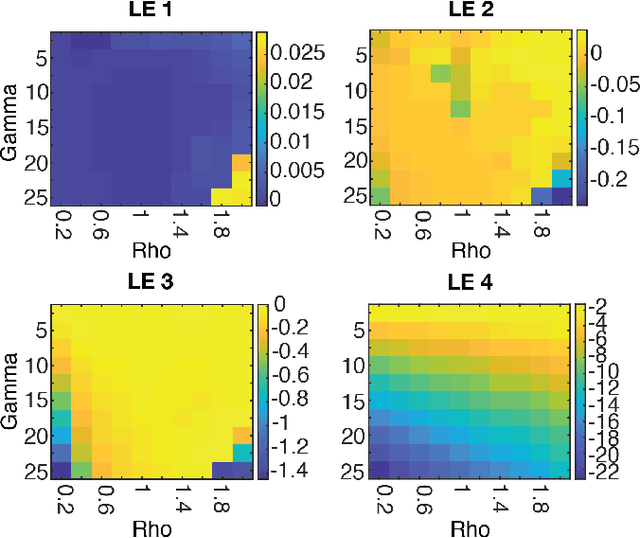
Neural systems are well known for their ability to learn and store information as memories. Even more impressive is their ability to abstract these memories to create complex internal representations, enabling advanced functions such as the spatial manipulation of mental representations. While recurrent neural networks (RNNs) are capable of representing complex information, the exact mechanisms of how dynamical neural systems perform abstraction are still not well-understood, thereby hindering the development of more advanced functions. Here, we train a 1000-neuron RNN -- a reservoir computer (RC) -- to abstract a continuous dynamical attractor memory from isolated examples of dynamical attractor memories. Further, we explain the abstraction mechanism with new theory. By training the RC on isolated and shifted examples of either stable limit cycles or chaotic Lorenz attractors, the RC learns a continuum of attractors, as quantified by an extra Lyapunov exponent equal to zero. We propose a theoretical mechanism of this abstraction by combining ideas from differentiable generalized synchronization and feedback dynamics. Our results quantify abstraction in simple neural systems, enabling us to design artificial RNNs for abstraction, and leading us towards a neural basis of abstraction.