Gaussian variational approximation with sparse precision matrices

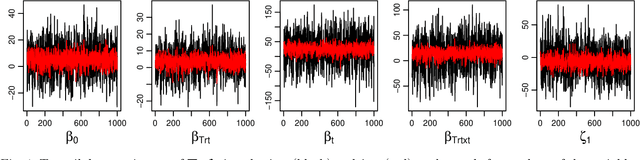
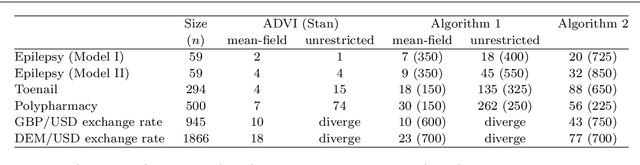
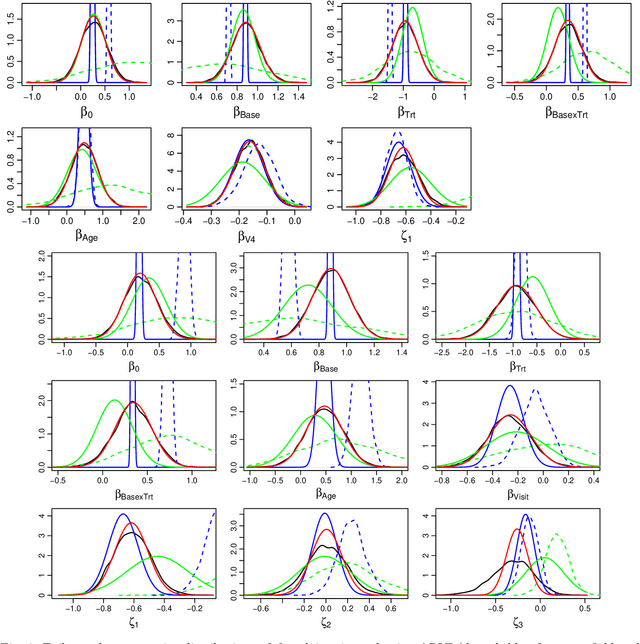
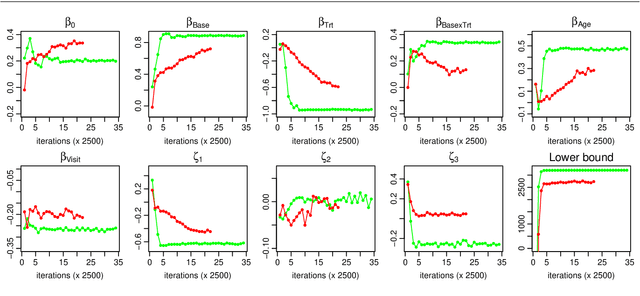
We consider the problem of learning a Gaussian variational approximation to the posterior distribution for a high-dimensional parameter, where we impose sparsity in the precision matrix to reflect appropriate conditional independence structure in the model. Incorporating sparsity in the precision matrix allows the Gaussian variational distribution to be both flexible and parsimonious, and the sparsity is achieved through parameterization in terms of the Cholesky factor. Efficient stochastic gradient methods which make appropriate use of gradient information for the target distribution are developed for the optimization. We consider alternative estimators of the stochastic gradients which have lower variation and are more stable. Our approach is illustrated using generalized linear mixed models and state space models for time series.

Topic-adjusted visibility metric for scientific articles

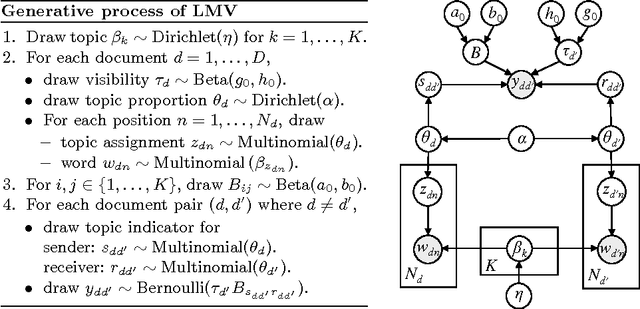
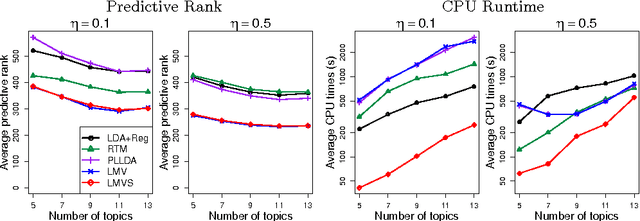
Measuring the impact of scientific articles is important for evaluating the research output of individual scientists, academic institutions and journals. While citations are raw data for constructing impact measures, there exist biases and potential issues if factors affecting citation patterns are not properly accounted for. In this work, we address the problem of field variation and introduce an article level metric useful for evaluating individual articles' visibility. This measure derives from joint probabilistic modeling of the content in the articles and the citations amongst them using latent Dirichlet allocation (LDA) and the mixed membership stochastic blockmodel (MMSB). Our proposed model provides a visibility metric for individual articles adjusted for field variation in citation rates, a structural understanding of citation behavior in different fields, and article recommendations which take into account article visibility and citation patterns. We develop an efficient algorithm for model fitting using variational methods. To scale up to large networks, we develop an online variant using stochastic gradient methods and case-control likelihood approximation. We apply our methods to the benchmark KDD Cup 2003 dataset with approximately 30,000 high energy physics papers.