PubSub-VFL: Towards Efficient Two-Party Split Learning in Heterogeneous Environments via Publisher/Subscriber Architecture

With the rapid advancement of the digital economy, data collaboration between organizations has become a well-established business model, driving the growth of various industries. However, privacy concerns make direct data sharing impractical. To address this, Two-Party Split Learning (a.k.a. Vertical Federated Learning (VFL)) has emerged as a promising solution for secure collaborative learning. Despite its advantages, this architecture still suffers from low computational resource utilization and training efficiency. Specifically, its synchronous dependency design increases training latency, while resource and data heterogeneity among participants further hinder efficient computation. To overcome these challenges, we propose PubSub-VFL, a novel VFL paradigm with a Publisher/Subscriber architecture optimized for two-party collaborative learning with high computational efficiency. PubSub-VFL leverages the decoupling capabilities of the Pub/Sub architecture and the data parallelism of the parameter server architecture to design a hierarchical asynchronous mechanism, reducing training latency and improving system efficiency. Additionally, to mitigate the training imbalance caused by resource and data heterogeneity, we formalize an optimization problem based on participants' system profiles, enabling the selection of optimal hyperparameters while preserving privacy. We conduct a theoretical analysis to demonstrate that PubSub-VFL achieves stable convergence and is compatible with security protocols such as differential privacy. Extensive case studies on five benchmark datasets further validate its effectiveness, showing that, compared to state-of-the-art baselines, PubSub-VFL not only accelerates training by $2 \sim 7\times$ without compromising accuracy, but also achieves a computational resource utilization rate of up to 91.07%.

Maximizing approximately k-submodular functions

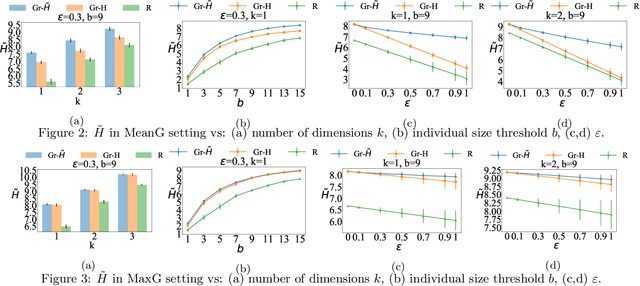
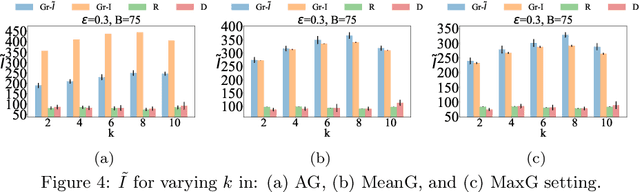
We introduce the problem of maximizing approximately $k$-submodular functions subject to size constraints. In this problem, one seeks to select $k$-disjoint subsets of a ground set with bounded total size or individual sizes, and maximum utility, given by a function that is "close" to being $k$-submodular. The problem finds applications in tasks such as sensor placement, where one wishes to install $k$ types of sensors whose measurements are noisy, and influence maximization, where one seeks to advertise $k$ topics to users of a social network whose level of influence is uncertain. To deal with the problem, we first provide two natural definitions for approximately $k$-submodular functions and establish a hierarchical relationship between them. Next, we show that simple greedy algorithms offer approximation guarantees for different types of size constraints. Last, we demonstrate experimentally that the greedy algorithms are effective in sensor placement and influence maximization problems.