A Geometric Theory of Cognition

Human cognition spans perception, memory, intuitive judgment, deliberative reasoning, action selection, and social inference, yet these capacities are often explained through distinct computational theories. Here we present a unified mathematical framework in which diverse cognitive processes emerge from a single geometric principle. We represent the cognitive state as a point on a differentiable manifold endowed with a learned Riemannian metric that encodes representational constraints, computational costs, and structural relations among cognitive variables. A scalar cognitive potential combines predictive accuracy, structural parsimony, task utility, and normative or logical requirements. Cognition unfolds as the Riemannian gradient flow of this potential, providing a universal dynamical law from which a broad range of psychological phenomena arise. Classical dual-process effects--rapid intuitive responses and slower deliberative reasoning--emerge naturally from metric-induced anisotropies that generate intrinsic time-scale separations and geometric phase transitions, without invoking modular or hybrid architectures. We derive analytical conditions for these regimes and demonstrate their behavioural signatures through simulations of canonical cognitive tasks. Together, these results establish a geometric foundation for cognition and suggest guiding principles for the development of more general and human-like artificial intelligence systems.

D3PG: Dirichlet DDGP for Task Partitioning and Offloading with Constrained Hybrid Action Space in Mobile Edge Computing

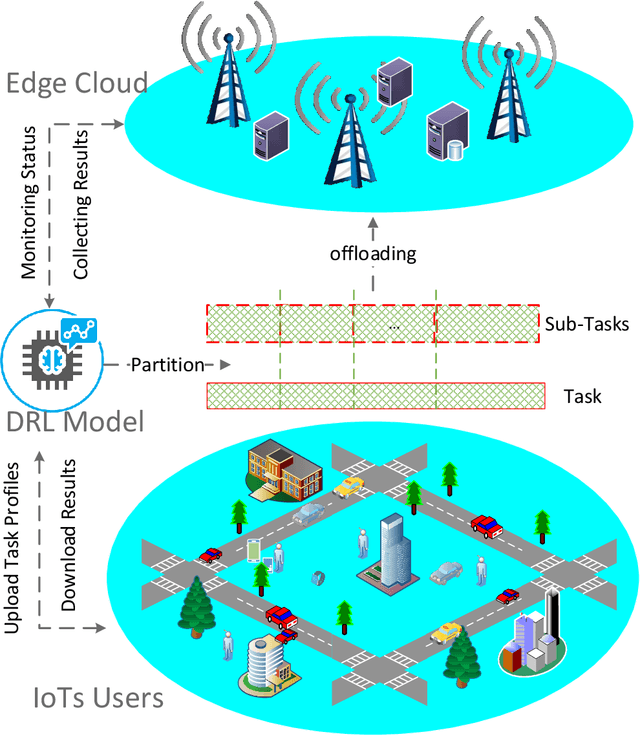
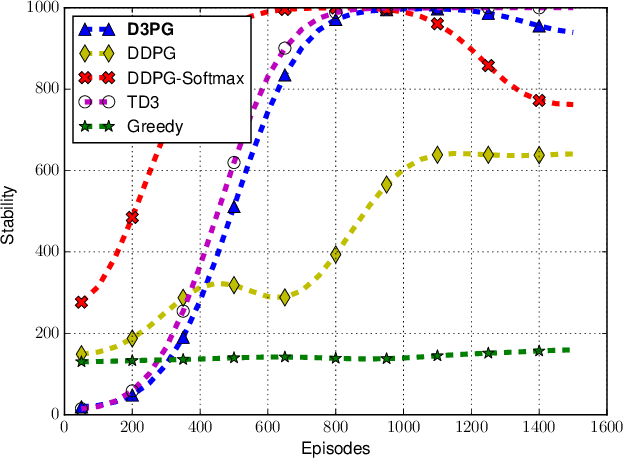
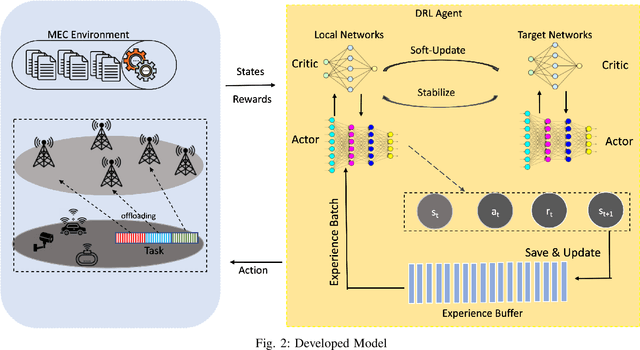
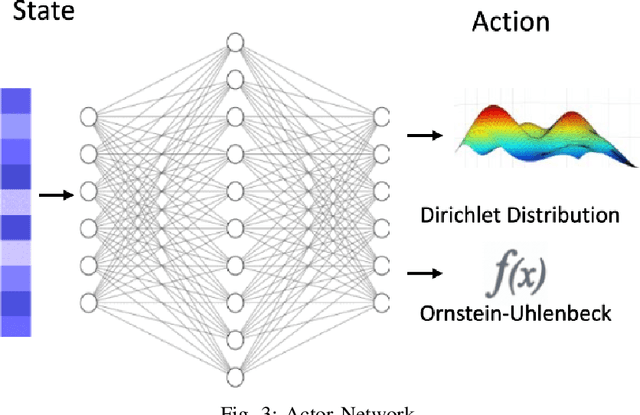
Mobile Edge Computing (MEC) has been regarded as a promising paradigm to reduce service latency for data processing in the Internet of Things, by provisioning computing resources at the network edge. In this work, we jointly optimize the task partitioning and computational power allocation for computation offloading in a dynamic environment with multiple IoT devices and multiple edge servers. We formulate the problem as a Markov decision process with constrained hybrid action space, which cannot be well handled by existing deep reinforcement learning (DRL) algorithms. Therefore, we develop a novel Deep Reinforcement Learning called Dirichlet Deep Deterministic Policy Gradient (D3PG), which is built on Deep Deterministic Policy Gradient (DDPG) to solve the problem. The developed model can learn to solve multi-objective optimization, including maximizing the number of tasks processed before expiration and minimizing the energy cost and service latency.} More importantly, D3PG can effectively deal with constrained distribution-continuous hybrid action space, where the distribution variables are for the task partitioning and offloading, while the continuous variables are for computational frequency control. Moreover, the D3PG can address many similar issues in MEC and general reinforcement learning problems. Extensive simulation results show that the proposed D3PG outperforms the state-of-art methods.