Set-Membership Estimation for Fault Diagnosis of Nonlinear Systems

This paper introduces a Fault Diagnosis (Detection, Isolation, and Estimation) method using Set-Membership Estimation (SME) designed for a class of nonlinear systems that are linear to the fault parameters. The methodology advances fault diagnosis by continuously evaluating an estimate of the fault parameter and a feasible parameter set where the true fault parameter belongs. Unlike previous SME approaches, in this work, we address nonlinear systems subjected to both input and output uncertainties by utilizing inclusion functions and interval arithmetic. Additionally, we present an approach to outer-approximate the polytopic description of the feasible parameter set by effectively balancing approximation accuracy with computational efficiency resulting in improved fault detectability. Lastly, we introduce adaptive regularization of the parameter estimates to enhance the estimation process when the input-output data are sparse or non-informative, enhancing fault identifiability. We demonstrate the effectiveness of this method in simulations involving an Autonomous Surface Vehicle in both a path-following and a realistic collision avoidance scenario, underscoring its potential to enhance safety and reliability in critical applications.

Globally Guided Trajectory Planning in Dynamic Environments

Navigating mobile robots through environments shared with humans is challenging. From the perspective of the robot, humans are dynamic obstacles that must be avoided. These obstacles make the collision-free space nonconvex, which leads to two distinct passing behaviors per obstacle (passing left or right). For local planners, such as receding-horizon trajectory optimization, each behavior presents a local optimum in which the planner can get stuck. This may result in slow or unsafe motion even when a better plan exists. In this work, we identify trajectories for multiple locally optimal driving behaviors, by considering their topology. This identification is made consistent over successive iterations by propagating the topology information. The most suitable high-level trajectory guides a local optimization-based planner, resulting in fast and safe motion plans. We validate the proposed planner on a mobile robot in simulation and real-world experiments.

Scenario-Based Trajectory Optimization in Uncertain Dynamic Environments

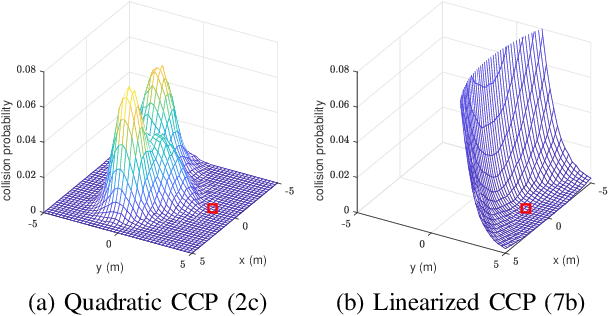
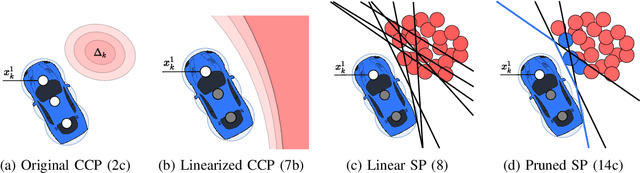
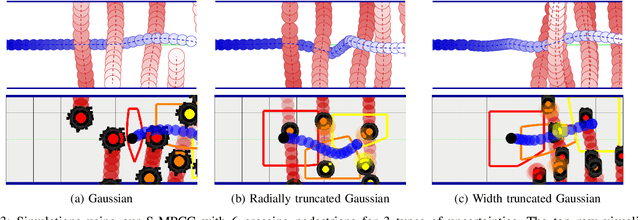
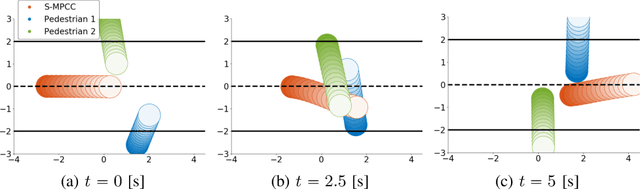
We present an optimization-based method to plan the motion of an autonomous robot under the uncertainties associated with dynamic obstacles, such as humans. Our method bounds the marginal risk of collisions at each point in time by incorporating chance constraints into the planning problem. This problem is not suitable for online optimization outright for arbitrary probability distributions. Hence, we sample from these chance constraints using an uncertainty model, to generate "scenarios", which translate the probabilistic constraints into deterministic ones. In practice, each scenario represents the collision constraint for a dynamic obstacle at the location of the sample. The number of theoretically required scenarios can be very large. Nevertheless, by exploiting the geometry of the workspace, we show how to prune most scenarios before optimization and we demonstrate how the reduced scenarios can still provide probabilistic guarantees on the safety of the motion plan. Since our approach is scenario based, we are able to handle arbitrary uncertainty distributions. We apply our method in a Model Predictive Contouring Control framework and demonstrate its benefits in simulations and experiments with a moving robot platform navigating among pedestrians, running in real-time.