Extension of Saaty's inconsistency index to incomplete comparisons: Approximated thresholds

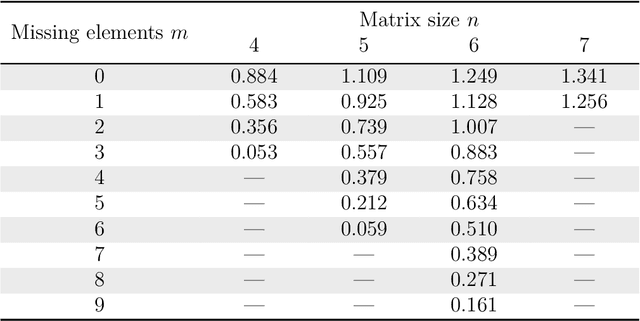
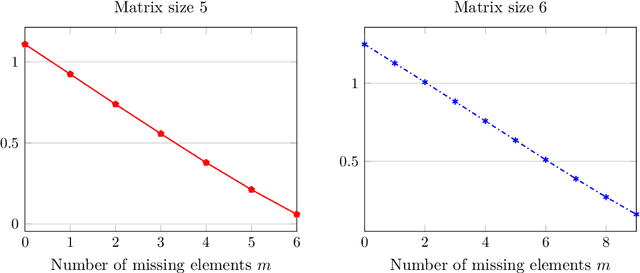
Pairwise comparison matrices are increasingly used in settings where some pairs are missing. However, there exist few inconsistency indices to analyse such incomplete data sets and even fewer measures have an associated threshold. This paper generalises the inconsistency index proposed by Saaty to incomplete pairwise comparison matrices. The extension is based on the approach of filling the missing elements to minimise the eigenvalue of the incomplete matrix. It means that the well-established values of the random index, a crucial component of the consistency ratio for which the famous threshold of 0.1 provides the condition for the acceptable level of inconsistency, cannot be directly adopted. The inconsistency of random matrices turns out to be the function of matrix size and the number of missing elements, with a nearly linear dependence in the case of the latter variable. Our results can be directly used by practitioners as a statistical criterion for accepting/rejecting an incomplete pairwise comparison matrix.

A revenue allocation scheme based on pairwise comparisons

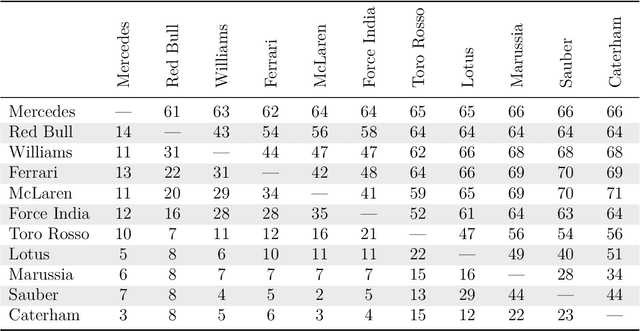
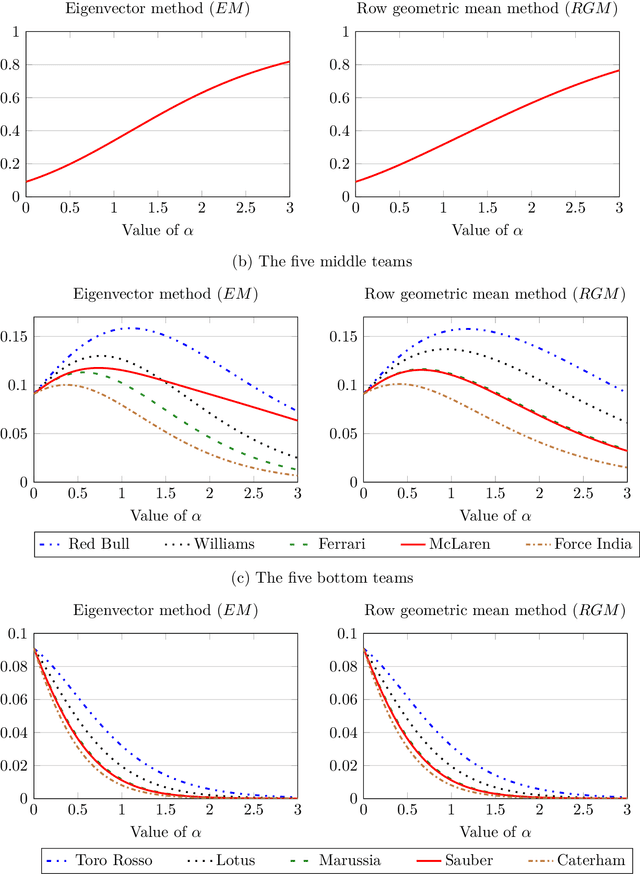
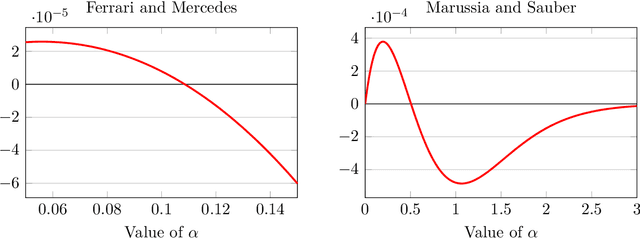
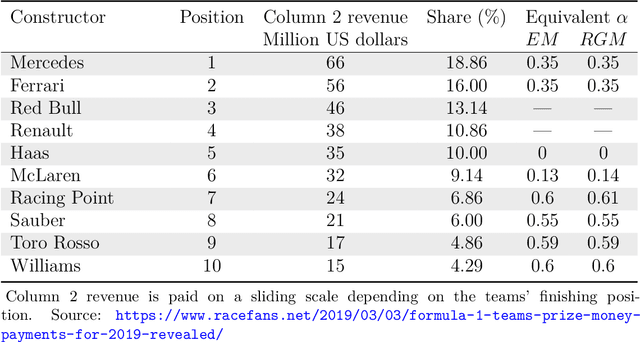
A model of sharing revenues among groups when group members are ranked several times is presented. The methodology is based on pairwise comparison matrices, allows for the use of any weighting method, and makes possible to tune the level of inequality. Our proposal is demonstrated on the example of Formula One prize money allocation among the constructors. We introduce an axiom called scale invariance, which requires the ranking of teams to be independent of the parameter controlling inequality. The eigenvector method is revealed to violate this condition in our dataset, while the row geometric mean method always satisfies it. The revenue allocation is not influenced by the arbitrary valuation given to the race prizes in the official points scoring system of Formula One.

Axiomatizations of inconsistency indices for triads

Pairwise comparison matrices often exhibit inconsistency, therefore, a number of indices has been introduced to measure their deviation from a consistent matrix. Since inconsistency first emerges in the case of three alternatives, several inconsistency indices are based on triads. Recently, a set of axioms has been proposed, and is required to be satisfied by any reasonable inconsistency index. We illustrate by an example that this set seems to be not exhaustive, hence expand it by adding two new properties. We consider all axioms on the set of triads, and choose the logically independent ones. Finally, it is proved that they characterize the inconsistency ranking induced by the Koczkodaj inconsistency index on this domain.

Characterization of an inconsistency ranking for pairwise comparison matrices

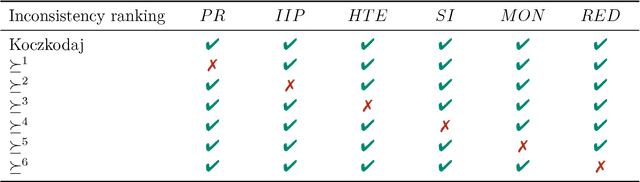
Pairwise comparisons between alternatives are a well-known method for measuring preferences of a decision-maker. Since these often do not exhibit consistency, a number of inconsistency indices has been introduced in order to measure the deviation from this ideal case. We axiomatically characterize the inconsistency ranking induced by the Koczkodaj inconsistency index: six independent properties are presented such that they determine a unique linear order on the set of all pairwise comparison matrices.

An application of incomplete pairwise comparison matrices for ranking top tennis players

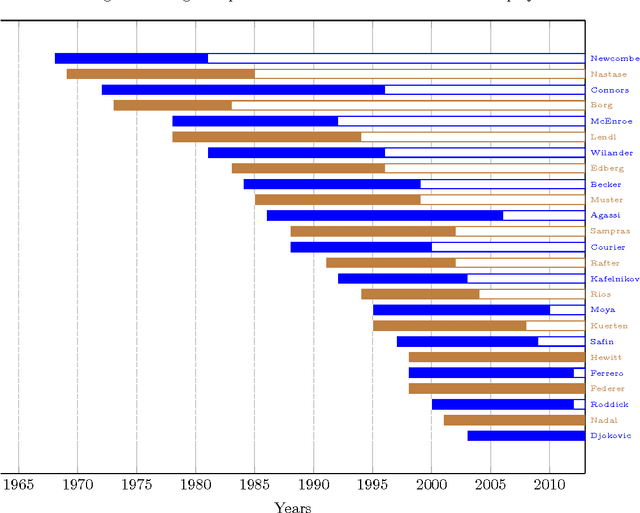
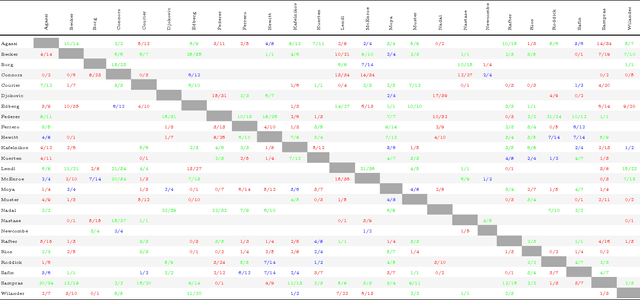
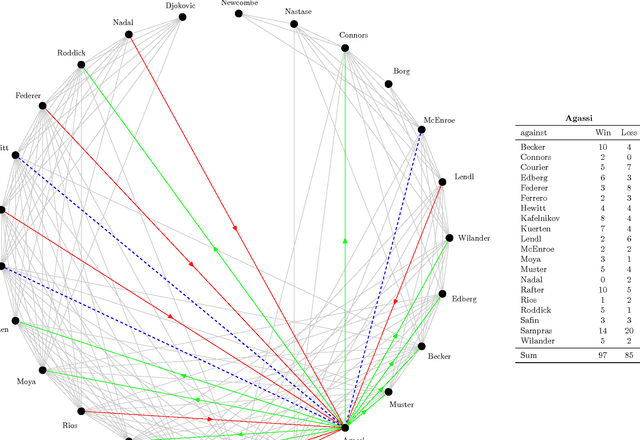
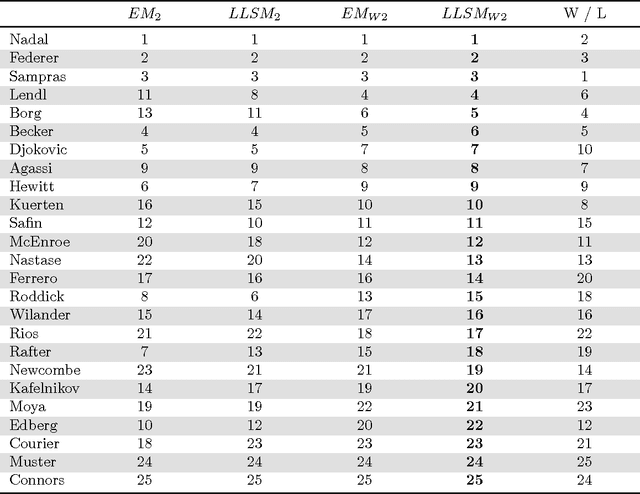
Pairwise comparison is an important tool in multi-attribute decision making. Pairwise comparison matrices (PCM) have been applied for ranking criteria and for scoring alternatives according to a given criterion. Our paper presents a special application of incomplete PCMs: ranking of professional tennis players based on their results against each other. The selected 25 players have been on the top of the ATP rankings for a shorter or longer period in the last 40 years. Some of them have never met on the court. One of the aims of the paper is to provide ranking of the selected players, however, the analysis of incomplete pairwise comparison matrices is also in the focus. The eigenvector method and the logarithmic least squares method were used to calculate weights from incomplete PCMs. In our results the top three players of four decades were Nadal, Federer and Sampras. Some questions have been raised on the properties of incomplete PCMs and remains open for further investigation.