Pose Estimation of a Thruster-Driven Bioinspired Multi-Link Robot

This work demonstrates pose (position and shape) estimation for a free-floating, bioinspired multi-link robot with unactuated joints, link-mounted thrusters for control, and a single gyroscope per link, resulting in an underactuated, minimally sensed platform. Through a proof-of-concept hardware experiment and offline Kalman filter analysis, we show that the robot's pose can be reliably estimated. State estimation is performed using an unscented Kalman filter augmented with Gaussian process residual learning to compensate for non-zero-mean, non-Gaussian noise. We further show that a filter trained on a multi-gait dataset (forward, backward, left, right, and turning) performs comparably to one trained on a larger forward-gait-only dataset when both are evaluated on the same forward-gait test trajectory. These results reveal overlap in the gait input space, which can be exploited to reduce training data requirements while enhancing the filter's generalizability across multiple gaits.

Nonlinear Modeling and Observability of a Planar Multi-Link Robot with Link Thrusters

This work is motivated by the development of cooperative teams of small, soft underwater robots designed to accomplish complex tasks through collective behavior. These robots take inspiration from biology: salps are gelatinous, jellyfish-like marine animals that utilize jet propulsion for maneuvering and can physically connect to form dynamic chains of arbitrary shape and size. The primary contributions of this research are twofold: first, we adapt a planar nonlinear multi-link snake robot model to model a planar multi-link salp-inspired system by removing joint actuators, introducing link thrusters, and allowing for non-uniform link lengths, masses, and moments of inertia. Second, we conduct a nonlinear observability analysis of the multi-link system with link thrusters, showing that the link angles, angular velocities, masses, and moments of inertia are locally observable when equipped with inertial measurement units and operating under specific thruster conditions. This research provides a theoretical foundation for modeling and estimating both the state and intrinsic parameters of a multi-link system with link thrusters, which are essential for effective controller design and performance.

Optimal Fiducial Marker Placement for Satellite Proximity Operations Using Observability Gramians

This paper investigates optimal fiducial marker placement on the surface of a satellite performing relative proximity operations with an observer satellite. The absolute and relative translation and attitude equations of motion for the satellite pair are modeled using dual quaternions. The observability of the relative dual quaternion system is analyzed using empirical observability Gramian methods. The optimal placement of a fiducial marker set, in which each marker gives simultaneous optical range and attitude measurements, is determined for the pair of satellites. A geostationary flyby between the observing body (chaser) and desired (target) satellites is numerically simulated and the optimal fiducial placement sets of five and ten on the surface of the desired satellite are solved. It is shown that the optimal solution maximizes the distance between fiducial markers and selects marker locations that are most sensitive to measuring changes in the state during the nonlinear trajectory, despite being visible for less time than other candidate marker locations. Definitions and properties of quaternions and dual quaternions, and parallels between the two, are presented alongside the relative motion model.

Relative Pose Observability Analysis Using Dual Quaternions

Relative pose (position and orientation) estimation is an essential component of many robotics applications. Fiducial markers, such as the AprilTag visual fiducial system, yield a relative pose measurement from a single marker detection and provide a powerful tool for pose estimation. In this paper, we perform a Lie algebraic nonlinear observability analysis on a nonlinear dual quaternion system that is composed of a relative pose measurement model and a relative motion model. We prove that many common dual quaternion expressions yield Jacobian matrices with advantageous block structures and rank properties that are beneficial for analysis. We show that using a dual quaternion representation yields an observability matrix with a simple block triangular structure and satisfies the necessary full rank condition.

On the sensitivity of pose estimation neural networks: rotation parameterizations, Lipschitz constants, and provable bounds

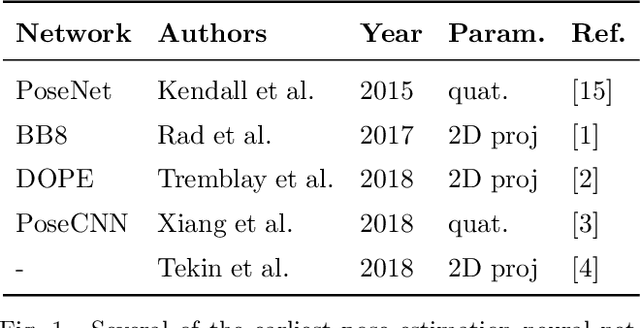
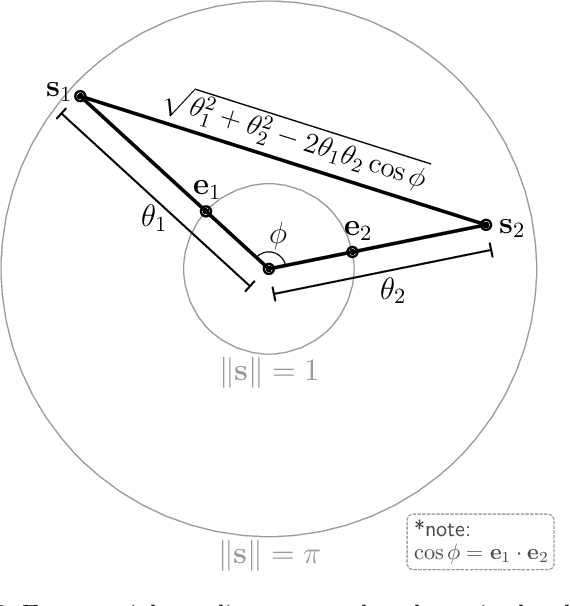
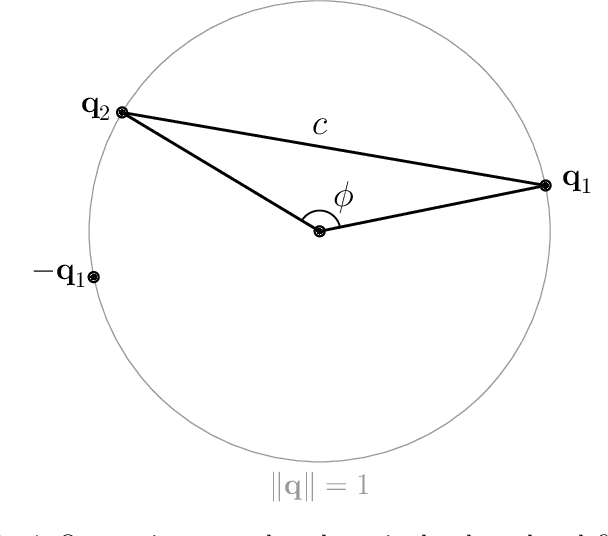
In this paper, we approach the task of determining sensitivity bounds for pose estimation neural networks. This task is particularly challenging as it requires characterizing the sensitivity of 3D rotations. We develop a sensitivity measure that describes the maximum rotational change in a network's output with respect to a Euclidean change in its input. We show that this measure is a type of Lipschitz constant, and that it is bounded by the product of a network's Euclidean Lipschitz constant and an intrinsic property of a rotation parameterization which we call the "distance ratio constant". We derive the distance ratio constant for several rotation parameterizations, and then discuss why the structure of most of these parameterizations makes it difficult to construct a pose estimation network with provable sensitivity bounds. However, we show that sensitivity bounds can be computed for networks which parameterize rotation using unconstrained exponential coordinates. We then construct and train such a network and compute sensitivity bounds for it.

Analytical bounds on the local Lipschitz constants of ReLU networks

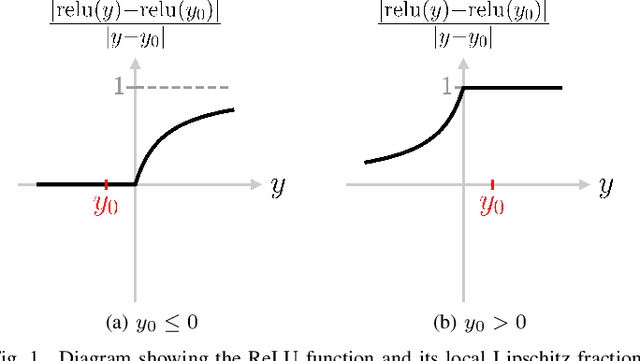
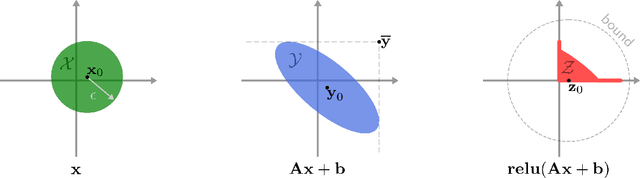
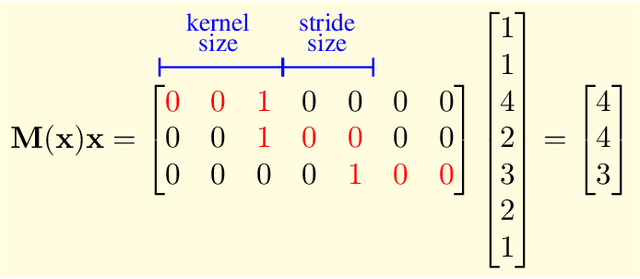
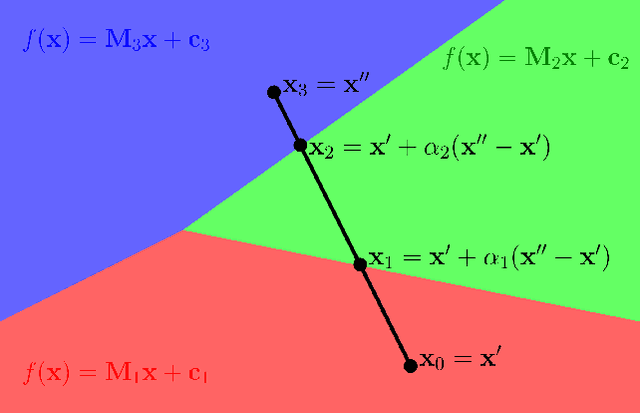
In this paper, we determine analytical upper bounds on the local Lipschitz constants of feedforward neural networks with ReLU activation functions. We do so by deriving Lipschitz constants and bounds for ReLU, affine-ReLU, and max pooling functions, and combining the results to determine a network-wide bound. Our method uses several insights to obtain tight bounds, such as keeping track of the zero elements of each layer, and analyzing the composition of affine and ReLU functions. Furthermore, we employ a careful computational approach which allows us to apply our method to large networks such as AlexNet and VGG-16. We present several examples using different networks, which show how our local Lipschitz bounds are tighter than the global Lipschitz bounds. We also show how our method can be applied to provide adversarial bounds for classification networks. These results show that our method produces the largest known bounds on minimum adversarial perturbations for large networks such as AlexNet and VGG-16.

Analytical bounds on the local Lipschitz constants of affine-ReLU functions

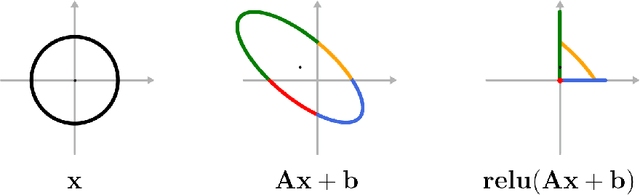
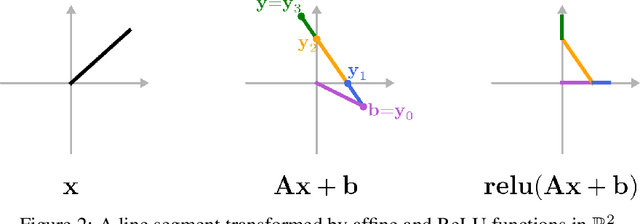
In this paper, we determine analytical bounds on the local Lipschitz constants of of affine functions composed with rectified linear units (ReLUs). Affine-ReLU functions represent a widely used layer in deep neural networks, due to the fact that convolution, fully-connected, and normalization functions are all affine, and are often followed by a ReLU activation function. Using an analytical approach, we mathematically determine upper bounds on the local Lipschitz constant of an affine-ReLU function, show how these bounds can be combined to determine a bound on an entire network, and discuss how the bounds can be efficiently computed, even for larger layers and networks. We show several examples by applying our results to AlexNet, as well as several smaller networks based on the MNIST and CIFAR-10 datasets. The results show that our method produces tighter bounds than the standard conservative bound (i.e. the product of the spectral norms of the layers' linear matrices), especially for small perturbations.