Reference Model of Multi-Entity Bayesian Networks for Predictive Situation Awareness

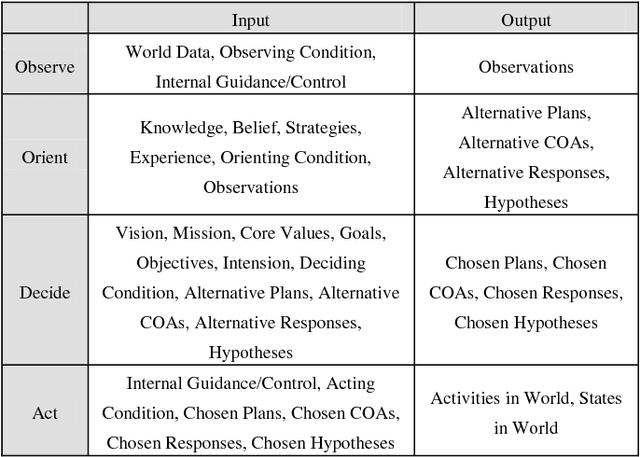
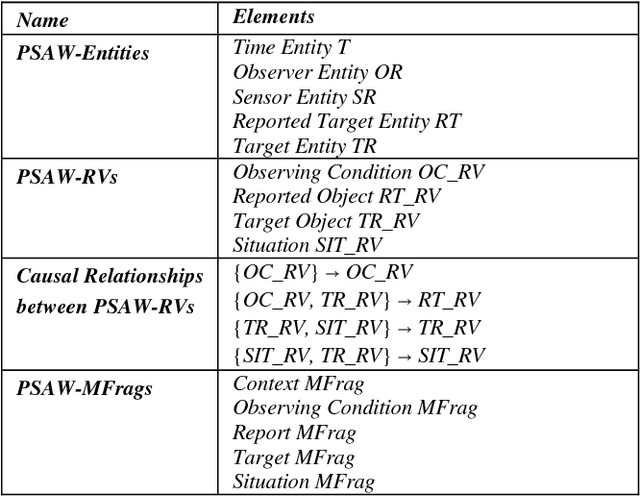
During the past quarter-century, situation awareness (SAW) has become a critical research theme, because of its importance. Since the concept of SAW was first introduced during World War I, various versions of SAW have been researched and introduced. Predictive Situation Awareness (PSAW) focuses on the ability to predict aspects of a temporally evolving situation over time. PSAW requires a formal representation and a reasoning method using such a representation. A Multi-Entity Bayesian Network (MEBN) is a knowledge representation formalism combining Bayesian Networks (BN) with First-Order Logic (FOL). MEBN can be used to represent uncertain situations (supported by BN) as well as complex situations (supported by FOL). Also, efficient reasoning algorithms for MEBN have been developed. MEBN can be a formal representation to support PSAW and has been used for several PSAW systems. Although several MEBN applications for PSAW exist, very little work can be found in the literature that attempts to generalize a MEBN model to support PSAW. In this research, we define a reference model for MEBN in PSAW, called a PSAW-MEBN reference model. The PSAW-MEBN reference model enables us to easily develop a MEBN model for PSAW by supporting the design of a MEBN model for PSAW. In this research, we introduce two example use cases using the PSAW-MEBN reference model to develop MEBN models to support PSAW: a Smart Manufacturing System and a Maritime Domain Awareness System.

MEBN-RM: A Mapping between Multi-Entity Bayesian Network and Relational Model

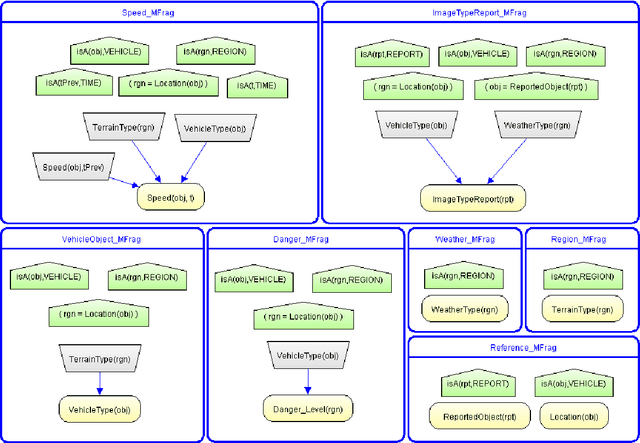
Multi-Entity Bayesian Network (MEBN) is a knowledge representation formalism combining Bayesian Networks (BN) with First-Order Logic (FOL). MEBN has sufficient expressive power for general-purpose knowledge representation and reasoning. Developing a MEBN model to support a given application is a challenge, requiring definition of entities, relationships, random variables, conditional dependence relationships, and probability distributions. When available, data can be invaluable both to improve performance and to streamline development. By far the most common format for available data is the relational database (RDB). Relational databases describe and organize data according to the Relational Model (RM). Developing a MEBN model from data stored in an RDB therefore requires mapping between the two formalisms. This paper presents MEBN-RM, a set of mapping rules between key elements of MEBN and RM. We identify links between the two languages (RM and MEBN) and define four levels of mapping from elements of RM to elements of MEBN. These definitions are implemented in the MEBN-RM algorithm, which converts a relational schema in RM to a partial MEBN model. Through this research, the software has been released as a MEBN-RM open-source software tool. The method is illustrated through two example use cases using MEBN-RM to develop MEBN models: a Critical Infrastructure Defense System and a Smart Manufacturing System.

Human-aided Multi-Entity Bayesian Networks Learning from Relational Data

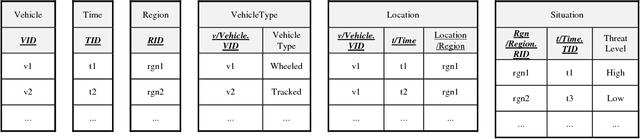
An Artificial Intelligence (AI) system is an autonomous system which emulates human mental and physical activities such as Observe, Orient, Decide, and Act, called the OODA process. An AI system performing the OODA process requires a semantically rich representation to handle a complex real world situation and ability to reason under uncertainty about the situation. Multi-Entity Bayesian Networks (MEBNs) combines First-Order Logic with Bayesian Networks for representing and reasoning about uncertainty in complex, knowledge-rich domains. MEBN goes beyond standard Bayesian networks to enable reasoning about an unknown number of entities interacting with each other in various types of relationships, a key requirement for the OODA process of an AI system. MEBN models have heretofore been constructed manually by a domain expert. However, manual MEBN modeling is labor-intensive and insufficiently agile. To address these problems, an efficient method is needed for MEBN modeling. One of the methods is to use machine learning to learn a MEBN model in whole or in part from data. In the era of Big Data, data-rich environments, characterized by uncertainty and complexity, have become ubiquitous. The larger the data sample is, the more accurate the results of the machine learning approach can be. Therefore, machine learning has potential to improve the quality of MEBN models as well as the effectiveness for MEBN modeling. In this research, we study a MEBN learning framework to develop a MEBN model from a combination of domain expert's knowledge and data. To evaluate the MEBN learning framework, we conduct an experiment to compare the MEBN learning framework and the existing manual MEBN modeling in terms of development efficiency.

Gaussian Mixture Reduction for Time-Constrained Approximate Inference in Hybrid Bayesian Networks

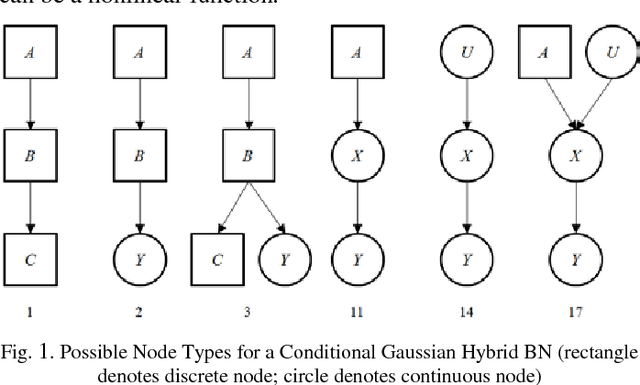
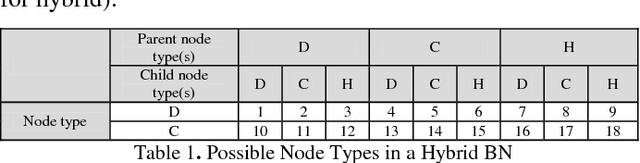
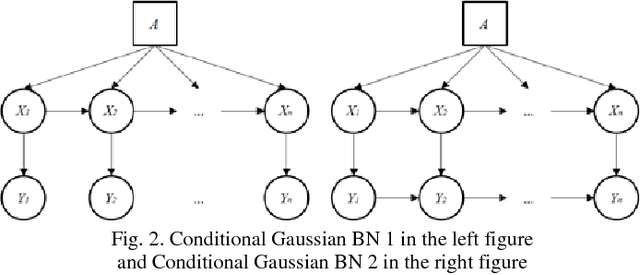
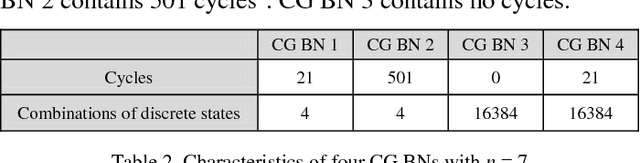
Hybrid Bayesian Networks (HBNs), which contain both discrete and continuous variables, arise naturally in many application areas (e.g., image understanding, data fusion, medical diagnosis, fraud detection). This paper concerns inference in an important subclass of HBNs, the conditional Gaussian (CG) networks, in which all continuous random variables have Gaussian distributions and all children of continuous random variables must be continuous. Inference in CG networks can be NP-hard even for special-case structures, such as poly-trees, where inference in discrete Bayesian networks can be performed in polynomial time. Therefore, approximate inference is required. In approximate inference, it is often necessary to trade off accuracy against solution time. This paper presents an extension to the Hybrid Message Passing inference algorithm for general CG networks and an algorithm for optimizing its accuracy given a bound on computation time. The extended algorithm uses Gaussian mixture reduction to prevent an exponential increase in the number of Gaussian mixture components. The trade-off algorithm performs pre-processing to find optimal run-time settings for the extended algorithm. Experimental results for four CG networks compare performance of the extended algorithm with existing algorithms and show the optimal settings for these CG networks.

An Application of Non-Monotonic Probabilistic Reasoning to Air Force Threat Correlation

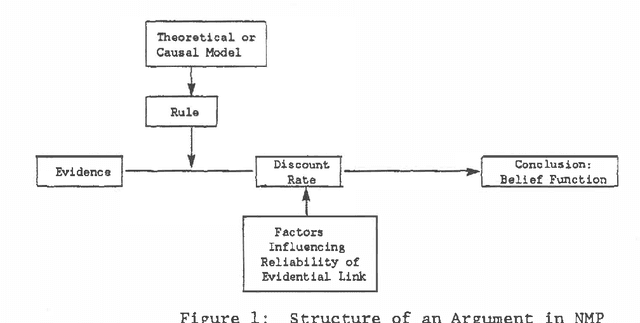
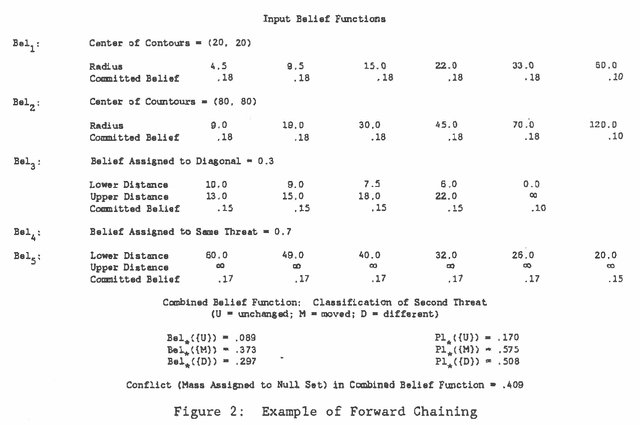
Current approaches to expert systems' reasoning under uncertainty fail to capture the iterative revision process characteristic of intelligent human reasoning. This paper reports on a system, called the Non-monotonic Probabilist, or NMP (Cohen, et al., 1985). When its inferences result in substantial conflict, NMP examines and revises the assumptions underlying the inferences until conflict is reduced to acceptable levels. NMP has been implemented in a demonstration computer-based system, described below, which supports threat correlation and in-flight route replanning by Air Force pilots.

Belief in Belief Functions: An Examination of Shafer's Canonical Examples

In the canonical examples underlying Shafer-Dempster theory, beliefs over the hypotheses of interest are derived from a probability model for a set of auxiliary hypotheses. Beliefs are derived via a compatibility relation connecting the auxiliary hypotheses to subsets of the primary hypotheses. A belief function differs from a Bayesian probability model in that one does not condition on those parts of the evidence for which no probabilities are specified. The significance of this difference in conditioning assumptions is illustrated with two examples giving rise to identical belief functions but different Bayesian probability distributions.

Hierarchical Evidence and Belief Functions

Dempster/Shafer (D/S) theory has been advocated as a way of representing incompleteness of evidence in a system's knowledge base. Methods now exist for propagating beliefs through chains of inference. This paper discusses how rules with attached beliefs, a common representation for knowledge in automated reasoning systems, can be transformed into the joint belief functions required by propagation algorithms. A rule is taken as defining a conditional belief function on the consequent given the antecedents. It is demonstrated by example that different joint belief functions may be consistent with a given set of rules. Moreover, different representations of the same rules may yield different beliefs on the consequent hypotheses.

A Probabilistic Reasoning Environment

A framework is presented for a computational theory of probabilistic argument. The Probabilistic Reasoning Environment encodes knowledge at three levels. At the deepest level are a set of schemata encoding the system's domain knowledge. This knowledge is used to build a set of second-level arguments, which are structured for efficient recapture of the knowledge used to construct them. Finally, at the top level is a Bayesian network constructed from the arguments. The system is designed to facilitate not just propagation of beliefs and assimilation of evidence, but also the dynamic process of constructing a belief network, evaluating its adequacy, and revising it when necessary.

Conflict and Surprise: Heuristics for Model Revision

Any probabilistic model of a problem is based on assumptions which, if violated, invalidate the model. Users of probability based decision aids need to be alerted when cases arise that are not covered by the aid's model. Diagnosis of model failure is also necessary to control dynamic model construction and revision. This paper presents a set of decision theoretically motivated heuristics for diagnosing situations in which a model is likely to provide an inadequate representation of the process being modeled.

The Bounded Bayesian

The ideal Bayesian agent reasons from a global probability model, but real agents are restricted to simplified models which they know to be adequate only in restricted circumstances. Very little formal theory has been developed to help fallibly rational agents manage the process of constructing and revising small world models. The goal of this paper is to present a theoretical framework for analyzing model management approaches. For a probability forecasting problem, a search process over small world models is analyzed as an approximation to a larger-world model which the agent cannot explicitly enumerate or compute. Conditions are given under which the sequence of small-world models converges to the larger-world probabilities.