Deep Koopman operator framework for causal discovery in nonlinear dynamical systems

We use a deep Koopman operator-theoretic formalism to develop a novel causal discovery algorithm, Kausal. Causal discovery aims to identify cause-effect mechanisms for better scientific understanding, explainable decision-making, and more accurate modeling. Standard statistical frameworks, such as Granger causality, lack the ability to quantify causal relationships in nonlinear dynamics due to the presence of complex feedback mechanisms, timescale mixing, and nonstationarity. This presents a challenge in studying many real-world systems, such as the Earth's climate. Meanwhile, Koopman operator methods have emerged as a promising tool for approximating nonlinear dynamics in a linear space of observables. In Kausal, we propose to leverage this powerful idea for causal analysis where optimal observables are inferred using deep learning. Causal estimates are then evaluated in a reproducing kernel Hilbert space, and defined as the distance between the marginal dynamics of the effect and the joint dynamics of the cause-effect observables. Our numerical experiments demonstrate Kausal's superior ability in discovering and characterizing causal signals compared to existing approaches of prescribed observables. Lastly, we extend our analysis to observations of El Ni\~no-Southern Oscillation highlighting our algorithm's applicability to real-world phenomena. Our code is available at https://github.com/juannat7/kausal.

Simulating the Air Quality Impact of Prescribed Fires Using a Graph Neural Network-Based PM$_{2.5}$ Emissions Forecasting System

The increasing size and severity of wildfires across western North America have generated dangerous levels of PM$_{2.5}$ pollution in recent years. In a warming climate, expanding the use of prescribed fires is widely considered to be the most robust fire mitigation strategy. However, reliably forecasting the potential air quality impact from these prescribed fires, a critical ingredient in determining the fires' location and time, at hourly to daily time scales remains a challenging problem. This paper proposes a novel integration of prescribed fire simulation with a spatio-temporal graph neural network-based PM$_{2.5}$ forecasting model. The experiments in this work focus on determining the optimal time for implementing prescribed fires in California as well as quantifying the potential air quality trade-offs involved in conducting more prescribed fires outside the fire season.

Correlation of Auroral Dynamics and GNSS Scintillation with an Autoencoder

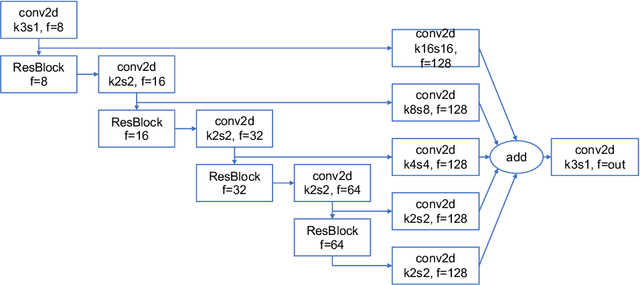
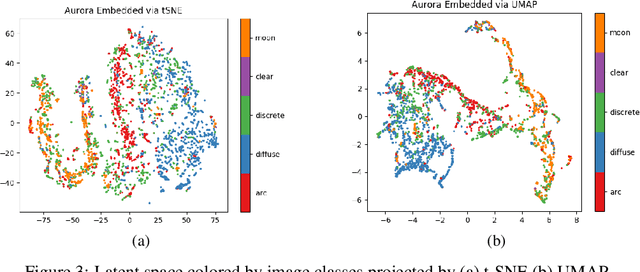
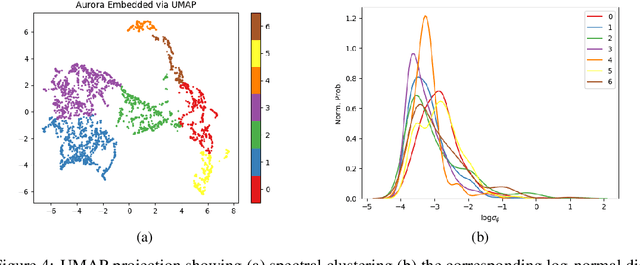
High energy particles originating from solar activity travel along the the Earth's magnetic field and interact with the atmosphere around the higher latitudes. These interactions often manifest as aurora in the form of visible light in the Earth's ionosphere. These interactions also result in irregularities in the electron density, which cause disruptions in the amplitude and phase of the radio signals from the Global Navigation Satellite Systems (GNSS), known as 'scintillation'. In this paper we use a multi-scale residual autoencoder (Res-AE) to show the correlation between specific dynamic structures of the aurora and the magnitude of the GNSS phase scintillations ($\sigma_{\phi}$). Auroral images are encoded in a lower dimensional feature space using the Res-AE, which in turn are clustered with t-SNE and UMAP. Both methods produce similar clusters, and specific clusters demonstrate greater correlations with observed phase scintillations. Our results suggest that specific dynamic structures of auroras are highly correlated with GNSS phase scintillations.

Prediction of GNSS Phase Scintillations: A Machine Learning Approach

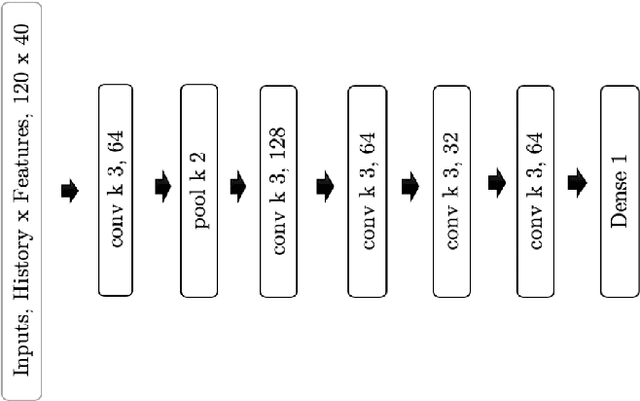
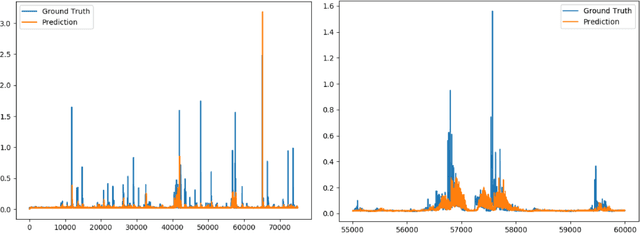
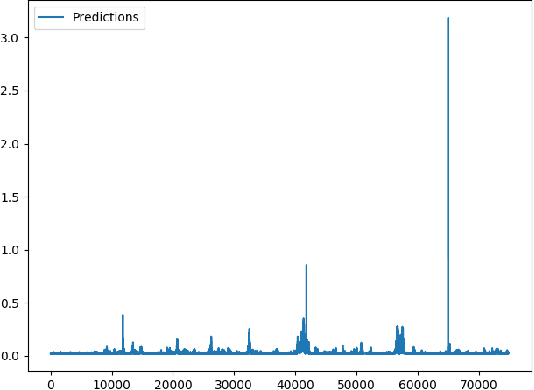
A Global Navigation Satellite System (GNSS) uses a constellation of satellites around the earth for accurate navigation, timing, and positioning. Natural phenomena like space weather introduce irregularities in the Earth's ionosphere, disrupting the propagation of the radio signals that GNSS relies upon. Such disruptions affect both the amplitude and the phase of the propagated waves. No physics-based model currently exists to predict the time and location of these disruptions with sufficient accuracy and at relevant scales. In this paper, we focus on predicting the phase fluctuations of GNSS radio waves, known as phase scintillations. We propose a novel architecture and loss function to predict 1 hour in advance the magnitude of phase scintillations within a time window of plus-minus 5 minutes with state-of-the-art performance.