Julia Ling
Turbulent scalar flux in inclined jets in crossflow: counter gradient transport and deep learning modelling
Jan 14, 2020
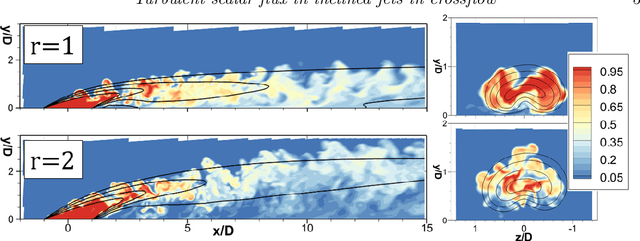
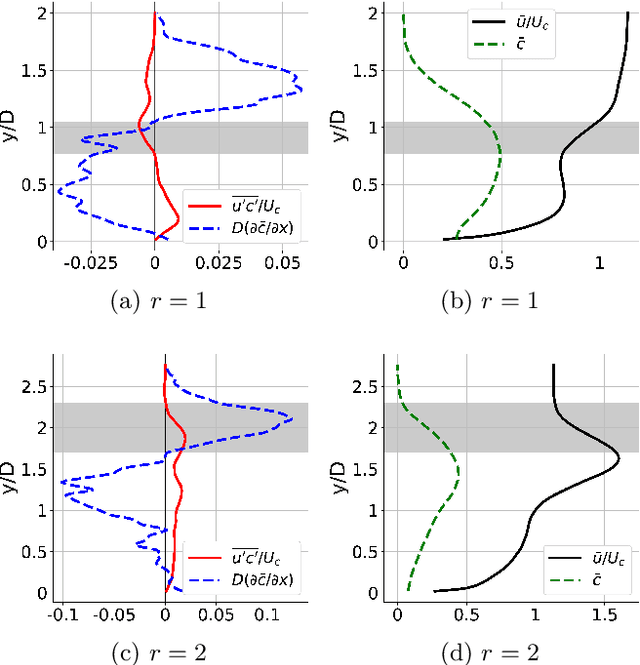
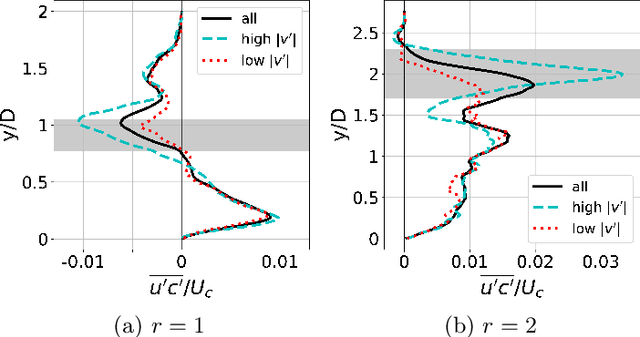
Abstract:A cylindrical and inclined jet in crossflow is studied under two distinct velocity ratios, $r=1$ and $r=2$, using highly resolved large eddy simulations (LES). First, an investigation of turbulent scalar mixing sheds light onto the previously observed but unexplained phenomenon of negative turbulent diffusivity. We identify two distinct types of counter gradient transport, prevalent in different regions: the first, throughout the windward shear layer, is caused by cross-gradient transport; the second, close to the wall right after injection, is caused by non-local effects. Then, we propose a deep learning approach for modelling the turbulent scalar flux by adapting the tensor basis neural network previously developed to model Reynolds stresses (Ling et al. 2016a). This approach uses a deep neural network with embedded coordinate frame invariance to predict a tensorial turbulent diffusivity that is not explicitly available in the high fidelity data used for training. After ensuring that the matrix diffusivity leads to a stable solution for the advection diffusion equation, we apply this approach in the inclined jets in crossflow under study. The results show significant improvement compared to a simple model, particularly where cross-gradient effects play an important role in turbulent mixing. The model proposed herein is not limited to jets in crossflow; it can be used in any turbulent flow where the Reynolds averaged transport of a scalar is considered.
Machine-learned metrics for predicting the likelihood of success in materials discovery
Nov 27, 2019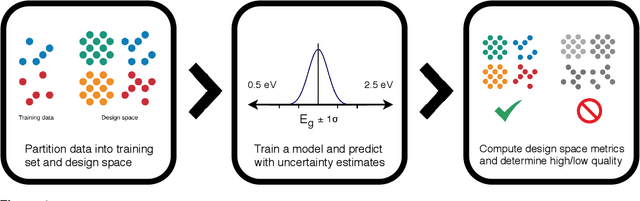
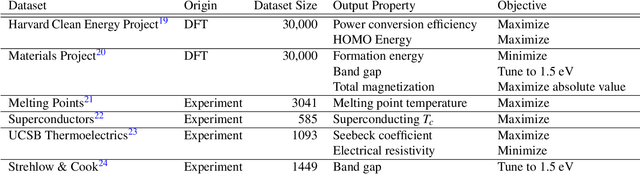
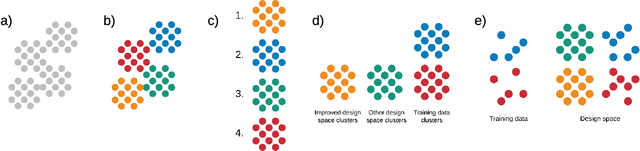
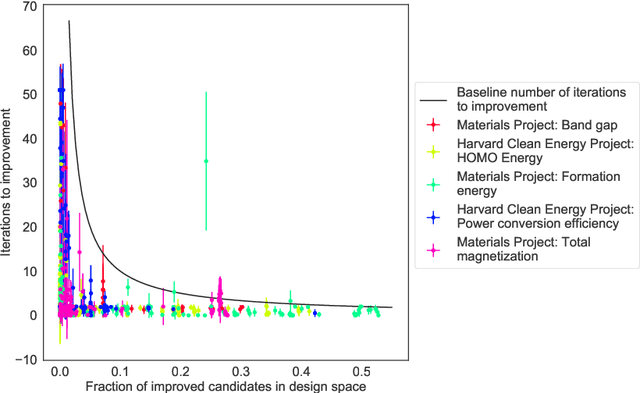
Abstract:Materials discovery is often compared to the challenge of finding a needle in a haystack. While much work has focused on accurately predicting the properties of candidate materials with machine learning (ML), which amounts to evaluating whether a given candidate is a piece of straw or a needle, less attention has been paid to a critical question: Are we searching in the right haystack? We refer to the haystack as the design space for a particular materials discovery problem (i.e. the set of possible candidate materials to synthesize), and thus frame this question as one of design space selection. In this paper, we introduce two metrics, the Predicted Fraction of Improved Candidates (PFIC), and the Cumulative Maximum Likelihood of Improvement (CMLI), which we demonstrate can identify discovery-rich and discovery-poor design spaces, respectively. Using CMLI and PFIC together to identify optimal design spaces can significantly accelerate ML-driven materials discovery.
Assessing the Frontier: Active Learning, Model Accuracy, and Multi-objective Materials Discovery and Optimization
Nov 06, 2019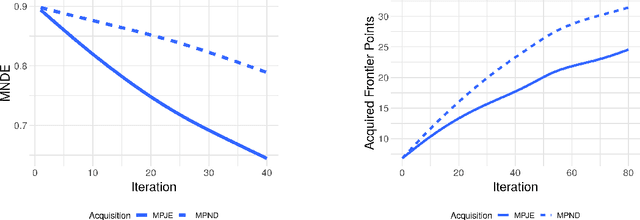

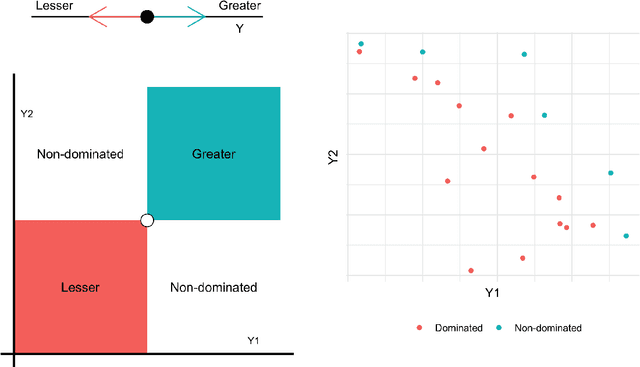
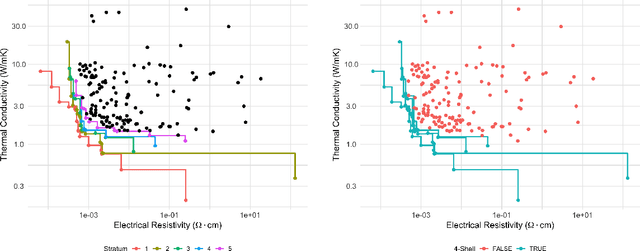
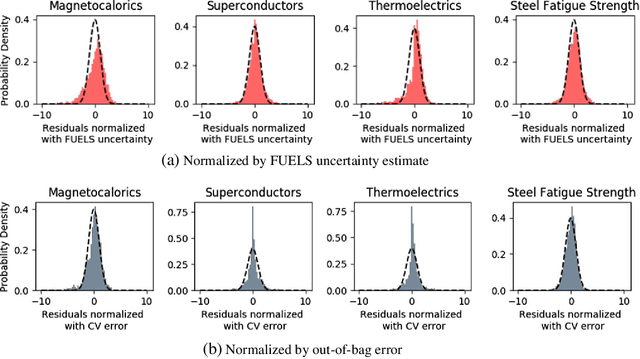
Abstract:Discovering novel materials can be greatly accelerated by iterative machine learning-informed proposal of candidates---active learning. However, standard \emph{global-scope error} metrics for model quality are not predictive of discovery performance, and can be misleading. We introduce the notion of \emph{Pareto shell-scope error} to help judge the suitability of a model for proposing material candidates. Further, through synthetic cases and a thermoelectric dataset, we probe the relation between acquisition function fidelity and active learning performance. Results suggest novel diagnostic tools, as well as new insights for acquisition function design.
Generalization of machine-learned turbulent heat flux models applied to film cooling flows
Oct 07, 2019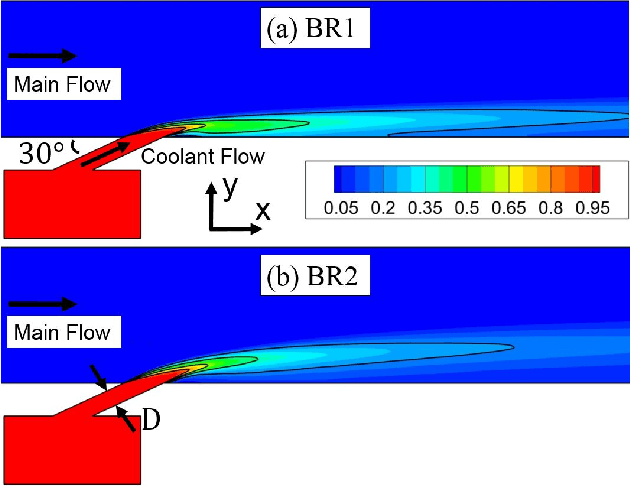

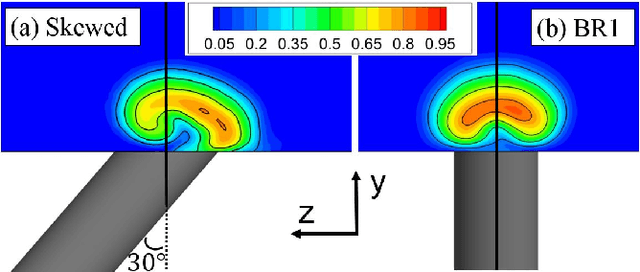
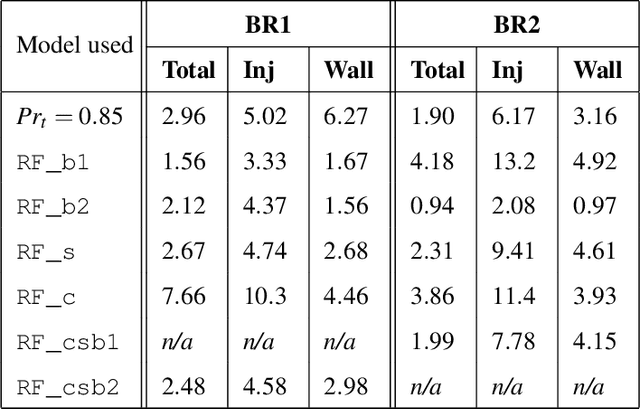
Abstract:The design of film cooling systems relies heavily on Reynolds-Averaged Navier-Stokes (RANS) simulations, which solve for mean quantities and model all turbulent scales. Most turbulent heat flux models, which are based on isotropic diffusion with a fixed turbulent Prandtl number ($Pr_t$), fail to accurately predict heat transfer in film cooling flows. In the present work, machine learning models are trained to predict a non-uniform $Pr_t$ field, using various datasets as training sets. The ability of these models to generalize beyond the flows on which they were trained is explored. Furthermore, visualization techniques are employed to compare distinct datasets and to help explain the cross-validation results.
Overcoming data scarcity with transfer learning
Nov 02, 2017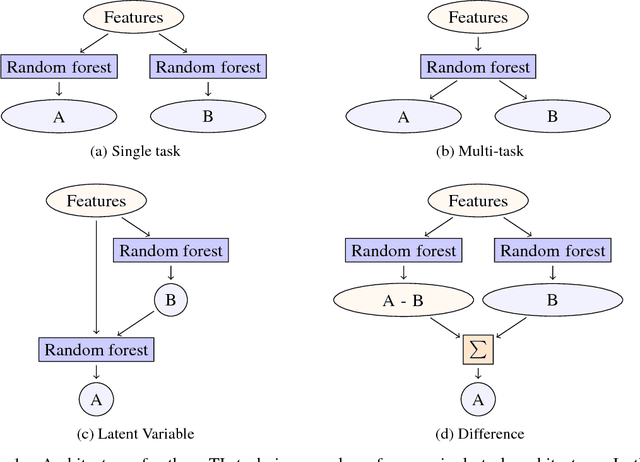
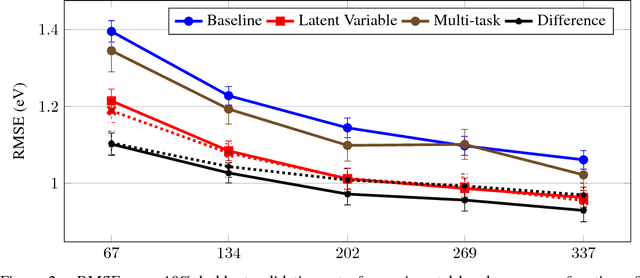
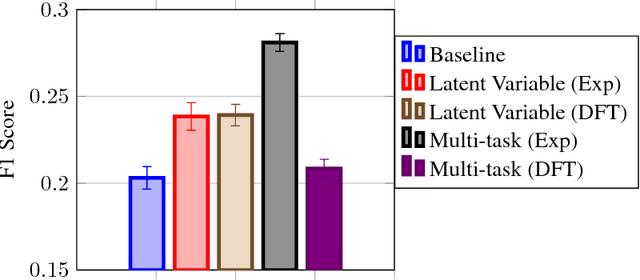
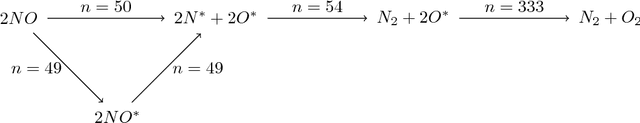
Abstract:Despite increasing focus on data publication and discovery in materials science and related fields, the global view of materials data is highly sparse. This sparsity encourages training models on the union of multiple datasets, but simple unions can prove problematic as (ostensibly) equivalent properties may be measured or computed differently depending on the data source. These hidden contextual differences introduce irreducible errors into analyses, fundamentally limiting their accuracy. Transfer learning, where information from one dataset is used to inform a model on another, can be an effective tool for bridging sparse data while preserving the contextual differences in the underlying measurements. Here, we describe and compare three techniques for transfer learning: multi-task, difference, and explicit latent variable architectures. We show that difference architectures are most accurate in the multi-fidelity case of mixed DFT and experimental band gaps, while multi-task most improves classification performance of color with band gaps. For activation energies of steps in NO reduction, the explicit latent variable method is not only the most accurate, but also enjoys cancellation of errors in functions that depend on multiple tasks. These results motivate the publication of high quality materials datasets that encode transferable information, independent of industrial or academic interest in the particular labels, and encourage further development and application of transfer learning methods to materials informatics problems.
Building Data-driven Models with Microstructural Images: Generalization and Interpretability
Nov 01, 2017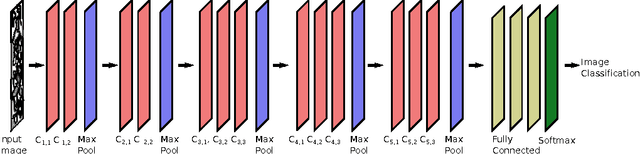
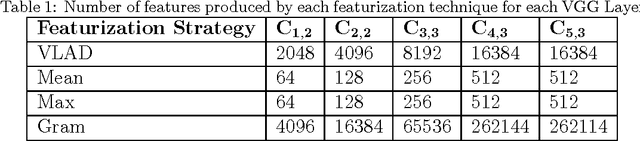
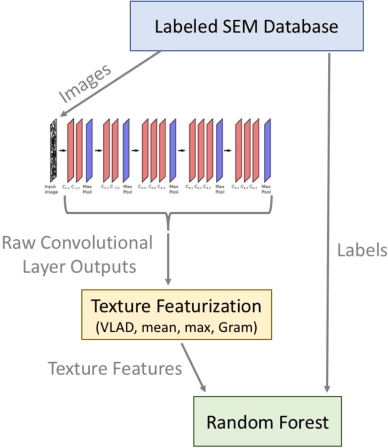
Abstract:As data-driven methods rise in popularity in materials science applications, a key question is how these machine learning models can be used to understand microstructure. Given the importance of process-structure-property relations throughout materials science, it seems logical that models that can leverage microstructural data would be more capable of predicting property information. While there have been some recent attempts to use convolutional neural networks to understand microstructural images, these early studies have focused only on which featurizations yield the highest machine learning model accuracy for a single data set. This paper explores the use of convolutional neural networks for classifying microstructure with a more holistic set of objectives in mind: generalization between data sets, number of features required, and interpretability.
High-Dimensional Materials and Process Optimization using Data-driven Experimental Design with Well-Calibrated Uncertainty Estimates
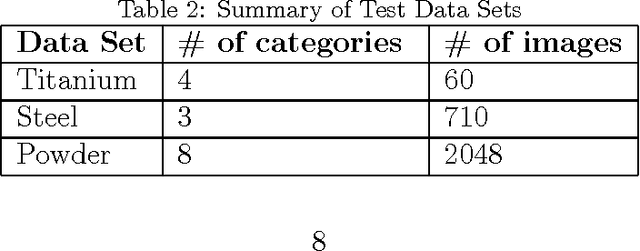
Jul 04, 2017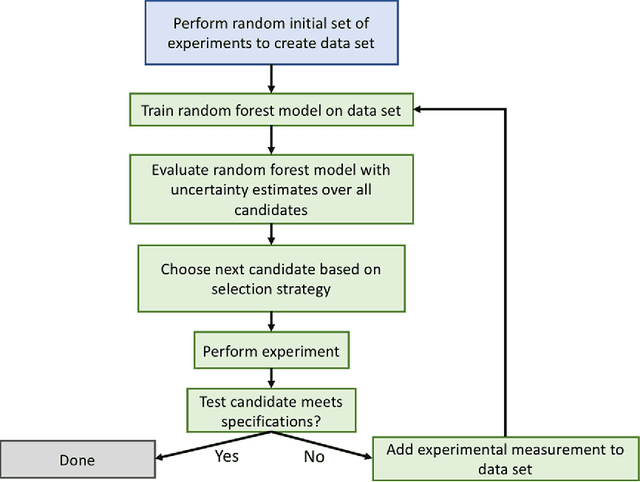

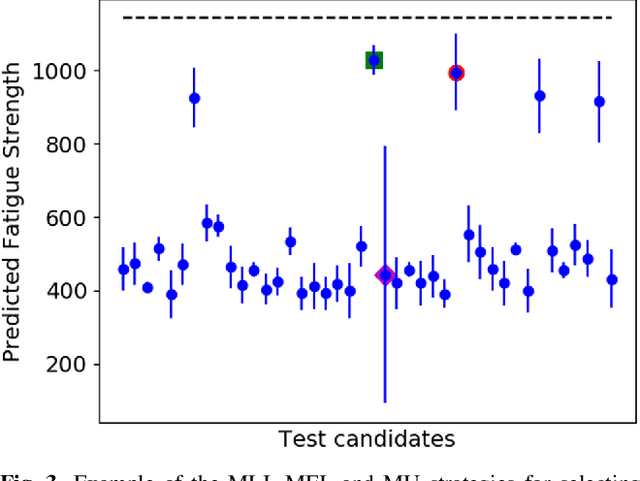
Abstract:The optimization of composition and processing to obtain materials that exhibit desirable characteristics has historically relied on a combination of scientist intuition, trial and error, and luck. We propose a methodology that can accelerate this process by fitting data-driven models to experimental data as it is collected to suggest which experiment should be performed next. This methodology can guide the scientist to test the most promising candidates earlier, and can supplement scientific intuition and knowledge with data-driven insights. A key strength of the proposed framework is that it scales to high-dimensional parameter spaces, as are typical in materials discovery applications. Importantly, the data-driven models incorporate uncertainty analysis, so that new experiments are proposed based on a combination of exploring high-uncertainty candidates and exploiting high-performing regions of parameter space. Over four materials science test cases, our methodology led to the optimal candidate being found with three times fewer required measurements than random guessing on average.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge