Improving Speech Decoding from ECoG with Self-Supervised Pretraining

Recent work on intracranial brain-machine interfaces has demonstrated that spoken speech can be decoded with high accuracy, essentially by treating the problem as an instance of supervised learning and training deep neural networks to map from neural activity to text. However, such networks pay for their expressiveness with very large numbers of labeled data, a requirement that is particularly burdensome for invasive neural recordings acquired from human patients. On the other hand, these patients typically produce speech outside of the experimental blocks used for training decoders. Making use of such data, and data from other patients, to improve decoding would ease the burden of data collection -- especially onerous for dys- and anarthric patients. Here we demonstrate that this is possible, by reengineering wav2vec -- a simple, self-supervised, fully convolutional model that learns latent representations of audio using a noise-contrastive loss -- for electrocorticographic (ECoG) data. We train this model on unlabelled ECoG recordings, and subsequently use it to transform ECoG from labeled speech sessions into wav2vec's representation space, before finally training a supervised encoder-decoder to map these representations to text. We experiment with various numbers of labeled blocks; for almost all choices, the new representations yield superior decoding performance to the original ECoG data, and in no cases do they yield worse. Performance can also be improved in some cases by pretraining wav2vec on another patient's data. In the best cases, wav2vec's representations decrease word error rates over the original data by upwards of 50%.

Learning Recurrent Models with Temporally Local Rules

Fitting generative models to sequential data typically involves two recursive computations through time, one forward and one backward. The latter could be a computation of the loss gradient (as in backpropagation through time), or an inference algorithm (as in the RTS/Kalman smoother). The backward pass in particular is computationally expensive (since it is inherently serial and cannot exploit GPUs), and difficult to map onto biological processes. Work-arounds have been proposed; here we explore a very different one: requiring the generative model to learn the joint distribution over current and previous states, rather than merely the transition probabilities. We show on toy datasets that different architectures employing this principle can learn aspects of the data typically requiring the backward pass.

Inferring Population Dynamics in Macaque Cortex

The proliferation of multi-unit cortical recordings over the last two decades, especially in macaques and during motor-control tasks, has generated interest in neural "population dynamics": the time evolution of neural activity across a group of neurons working together. A good model of these dynamics should be able to infer the activity of unobserved neurons within the same population and of the observed neurons at future times. Accordingly, Pandarinath and colleagues have introduced a benchmark to evaluate models on these two (and related) criteria: four data sets, each consisting of firing rates from a population of neurons, recorded from macaque cortex during movement-related tasks. Here we show that simple, general-purpose architectures based on recurrent neural networks (RNNs) outperform more "bespoke" models, and indeed outperform all published models on all four data sets in the benchmark. Performance can be improved further still with a novel, hybrid architecture that augments the RNN with self-attention, as in transformer networks. But pure transformer models fail to achieve this level of performance, either in our work or that of other groups. We argue that the autoregressive bias imposed by RNNs is critical for achieving the highest levels of performance. We conclude, however, by proposing that the benchmark be augmented with an alternative evaluation of latent dynamics that favors generative over discriminative models like the ones we propose in this report.

An Introduction to Modern Statistical Learning

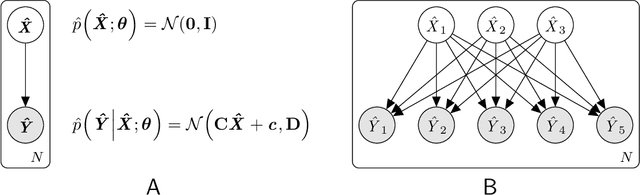
This work in progress aims to provide a unified introduction to statistical learning, building up slowly from classical models like the GMM and HMM to modern neural networks like the VAE and diffusion models. There are today many internet resources that explain this or that new machine-learning algorithm in isolation, but they do not (and cannot, in so brief a space) connect these algorithms with each other or with the classical literature on statistical models, out of which the modern algorithms emerged. Also conspicuously lacking is a single notational system which, although unfazing to those already familiar with the material (like the authors of these posts), raises a significant barrier to the novice's entry. Likewise, I have aimed to assimilate the various models, wherever possible, to a single framework for inference and learning, showing how (and why) to change one model into another with minimal alteration (some of them novel, others from the literature). Some background is of course necessary. I have assumed the reader is familiar with basic multivariable calculus, probability and statistics, and linear algebra. The goal of this book is certainly not completeness, but rather to draw a more or less straight-line path from the basics to the extremely powerful new models of the last decade. The goal then is to complement, not replace, such comprehensive texts as Bishop's \emph{Pattern Recognition and Machine Learning}, which is now 15 years old.

Recurrent Exponential-Family Harmoniums without Backprop-Through-Time

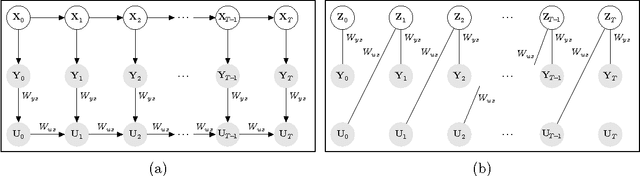
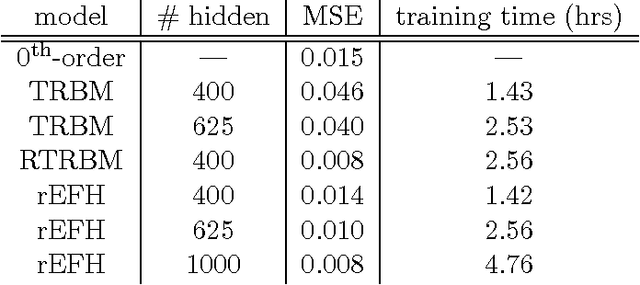
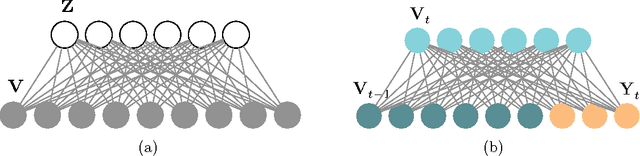
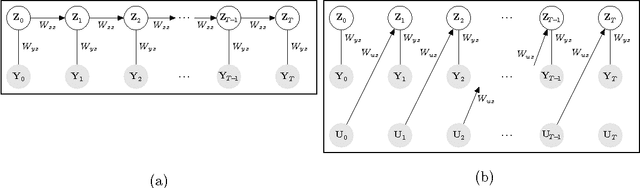
Exponential-family harmoniums (EFHs), which extend restricted Boltzmann machines (RBMs) from Bernoulli random variables to other exponential families (Welling et al., 2005), are generative models that can be trained with unsupervised-learning techniques, like contrastive divergence (Hinton et al. 2006; Hinton, 2002), as density estimators for static data. Methods for extending RBMs--and likewise EFHs--to data with temporal dependencies have been proposed previously (Sutskever and Hinton, 2007; Sutskever et al., 2009), the learning procedure being validated by qualitative assessment of the generative model. Here we propose and justify, from a very different perspective, an alternative training procedure, proving sufficient conditions for optimal inference under that procedure. The resulting algorithm can be learned with only forward passes through the data--backprop-through-time is not required, as in previous approaches. The proof exploits a recent result about information retention in density estimators (Makin and Sabes, 2015), and applies it to a "recurrent EFH" (rEFH) by induction. Finally, we demonstrate optimality by simulation, testing the rEFH: (1) as a filter on training data generated with a linear dynamical system, the position of which is noisily reported by a population of "neurons" with Poisson-distributed spike counts; and (2) with the qualitative experiments proposed by Sutskever et al. (2009).