Sampling from multimodal distributions using tempered Hamiltonian transitions

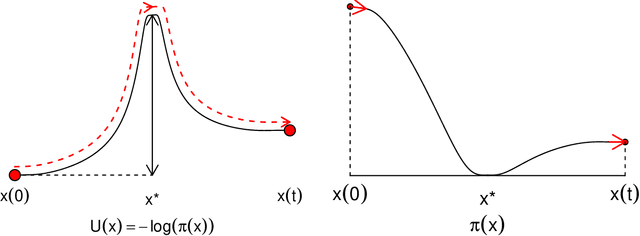
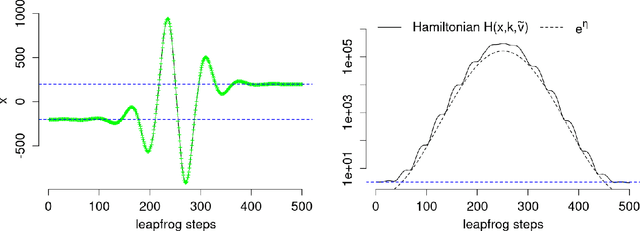
Hamiltonian Monte Carlo (HMC) methods are widely used to draw samples from unnormalized target densities due to high efficiency and favorable scalability with respect to increasing space dimensions. However, HMC struggles when the target distribution is multimodal, because the maximum increase in the potential energy function (i.e., the negative log density function) along the simulated path is bounded by the initial kinetic energy, which follows a half of the $\chi_d^2$ distribution, where d is the space dimension. In this paper, we develop a Hamiltonian Monte Carlo method where the constructed paths can travel across high potential energy barriers. This method does not require the modes of the target distribution to be known in advance. Our approach enables frequent jumps between the isolated modes of the target density by continuously varying the mass of the simulated particle while the Hamiltonian path is constructed. Thus, this method can be considered as a combination of HMC and the tempered transitions method. Compared to other tempering methods, our method has a distinctive advantage in the Gibbs sampler settings, where the target distribution changes at each step. We develop a practical tuning strategy for our method and demonstrate that it can construct globally mixing Markov chains targeting high-dimensional, multimodal distributions, using mixtures of normals and a sensor network localization problem.

Markov chain Monte Carlo algorithms with sequential proposals

We explore a general framework in Markov chain Monte Carlo (MCMC) sampling where sequential proposals are tried as a candidate for the next state of the Markov chain. This sequential-proposal framework can be applied to various existing MCMC methods, including Metropolis-Hastings algorithms using random proposals and methods that use deterministic proposals such as Hamiltonian Monte Carlo (HMC) or the bouncy particle sampler. Sequential-proposal MCMC methods construct the same Markov chains as those constructed by the delayed rejection method under certain circumstances. In the context of HMC, the sequential-proposal approach has been proposed as extra chance generalized hybrid Monte Carlo (XCGHMC). We develop two novel methods in which the trajectories leading to proposals in HMC are automatically tuned to avoid doubling back, as in the No-U-Turn sampler (NUTS). The numerical efficiency of these new methods compare favorably to the NUTS. We additionally show that the sequential-proposal bouncy particle sampler enables the constructed Markov chain to pass through regions of low target density and thus facilitates better mixing of the chain when the target density is multimodal.