Natural Language, AI, and Quantum Computing in 2024: Research Ingredients and Directions in QNLP

Language processing is at the heart of current developments in artificial intelligence, and quantum computers are becoming available at the same time. This has led to great interest in quantum natural language processing, and several early proposals and experiments. This paper surveys the state of this area, showing how NLP-related techniques including word embeddings, sequential models, attention, and grammatical parsing have been used in quantum language processing. We introduce a new quantum design for the basic task of text encoding (representing a string of characters in memory), which has not been addressed in detail before. As well as motivating new technologies, quantum theory has made key contributions to the challenging questions of 'What is uncertainty?' and 'What is intelligence?' As these questions are taking on fresh urgency with artificial systems, the paper also considers some of the ways facts are conceptualized and presented in language. In particular, we argue that the problem of 'hallucinations' arises through a basic misunderstanding: language expresses any number of plausible hypotheses, only a few of which become actual, a distinction that is ignored in classical mechanics, but present (albeit confusing) in quantum mechanics.

KrADagrad: Kronecker Approximation-Domination Gradient Preconditioned Stochastic Optimization

Second order stochastic optimizers allow parameter update step size and direction to adapt to loss curvature, but have traditionally required too much memory and compute for deep learning. Recently, Shampoo [Gupta et al., 2018] introduced a Kronecker factored preconditioner to reduce these requirements: it is used for large deep models [Anil et al., 2020] and in production [Anil et al., 2022]. However, it takes inverse matrix roots of ill-conditioned matrices. This requires 64-bit precision, imposing strong hardware constraints. In this paper, we propose a novel factorization, Kronecker Approximation-Domination (KrAD). Using KrAD, we update a matrix that directly approximates the inverse empirical Fisher matrix (like full matrix AdaGrad), avoiding inversion and hence 64-bit precision. We then propose KrADagrad$^\star$, with similar computational costs to Shampoo and the same regret. Synthetic ill-conditioned experiments show improved performance over Shampoo for 32-bit precision, while for several real datasets we have comparable or better generalization.

SKI to go Faster: Accelerating Toeplitz Neural Networks via Asymmetric Kernels

Toeplitz Neural Networks (TNNs) (Qin et. al. 2023) are a recent sequence model with impressive results. They require O(n log n) computational complexity and O(n) relative positional encoder (RPE) multi-layer perceptron (MLP) and decay bias calls. We aim to reduce both. We first note that the RPE is a non-SPD (symmetric positive definite) kernel and the Toeplitz matrices are pseudo-Gram matrices. Further 1) the learned kernels display spiky behavior near the main diagonals with otherwise smooth behavior; 2) the RPE MLP is slow. For bidirectional models, this motivates a sparse plus low-rank Toeplitz matrix decomposition. For the sparse component's action, we do a small 1D convolution. For the low rank component, we replace the RPE MLP with linear interpolation and use asymmetric Structured Kernel Interpolation (SKI) (Wilson et. al. 2015) for O(n) complexity: we provide rigorous error analysis. For causal models, "fast" causal masking (Katharopoulos et. al. 2020) negates SKI's benefits. Working in the frequency domain, we avoid an explicit decay bias. To enforce causality, we represent the kernel via the real part of its frequency response using the RPE and compute the imaginary part via a Hilbert transform. This maintains O(n log n) complexity but achieves an absolute speedup. Modeling the frequency response directly is also competitive for bidirectional training, using one fewer FFT. We set a speed state of the art on Long Range Arena (Tay et. al. 2020) with minimal score degradation.

Single Index Latent Variable Models for Network Topology Inference

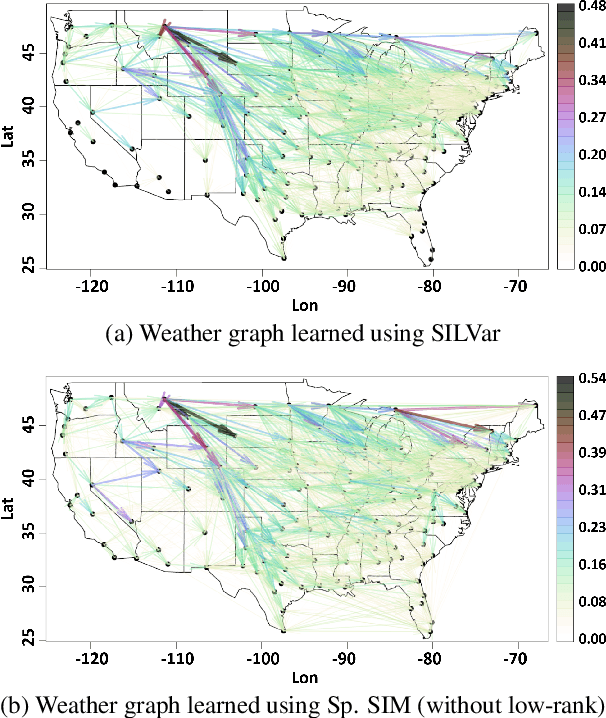
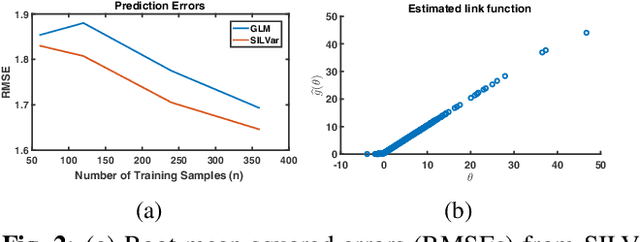
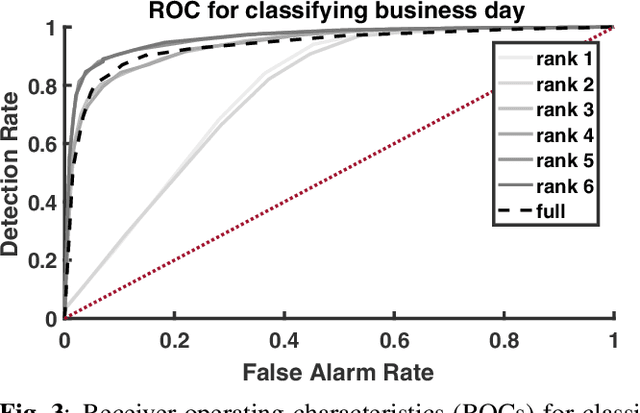
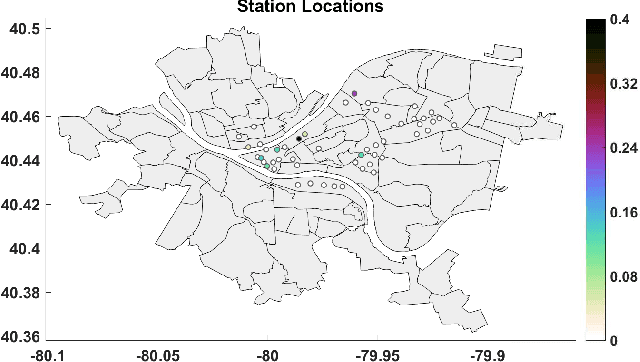
A semi-parametric, non-linear regression model in the presence of latent variables is applied towards learning network graph structure. These latent variables can correspond to unmodeled phenomena or unmeasured agents in a complex system of interacting entities. This formulation jointly estimates non-linearities in the underlying data generation, the direct interactions between measured entities, and the indirect effects of unmeasured processes on the observed data. The learning is posed as regularized empirical risk minimization. Details of the algorithm for learning the model are outlined. Experiments demonstrate the performance of the learned model on real data.

EigenNetworks

In many applications, the interdependencies among a set of $N$ time series $\{ x_{nk}, k>0 \}_{n=1}^{N}$ are well captured by a graph or network $G$. The network itself may change over time as well (i.e., as $G_k$). We expect the network changes to be at a much slower rate than that of the time series. This paper introduces eigennetworks, networks that are building blocks to compose the actual networks $G_k$ capturing the dependencies among the time series. These eigennetworks can be estimated by first learning the time series of graphs $G_k$ from the data, followed by a Principal Network Analysis procedure. Algorithms for learning both the original time series of graphs and the eigennetworks are presented and discussed. Experiments on simulated and real time series data demonstrate the performance of the learning and the interpretation of the eigennetworks.

SILVar: Single Index Latent Variable Models

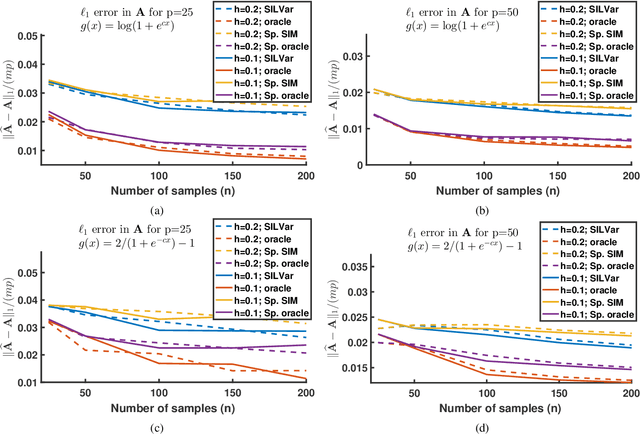
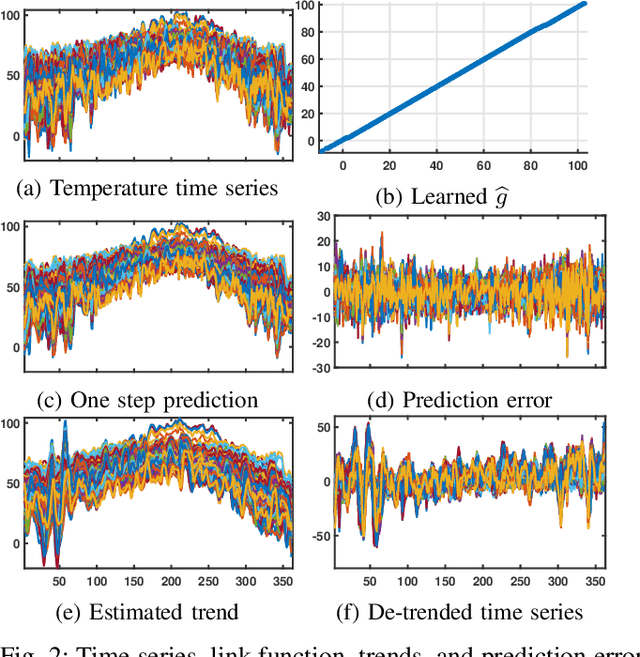
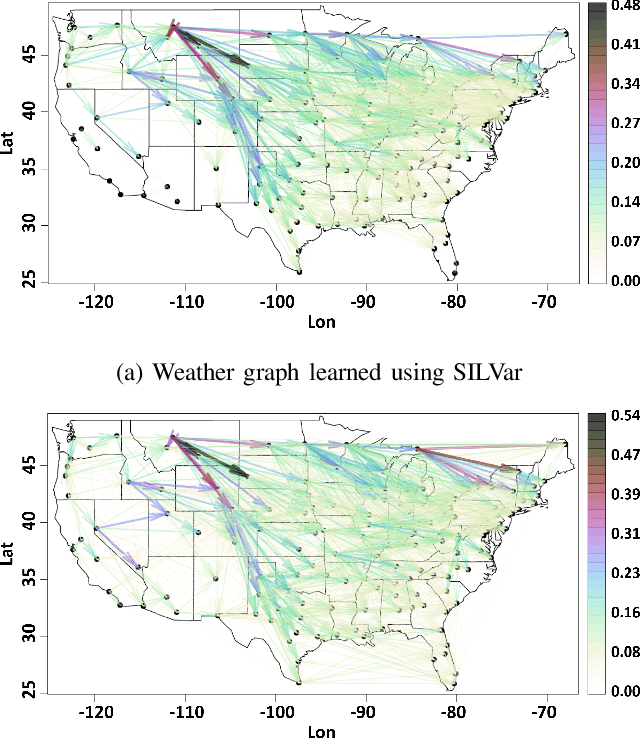
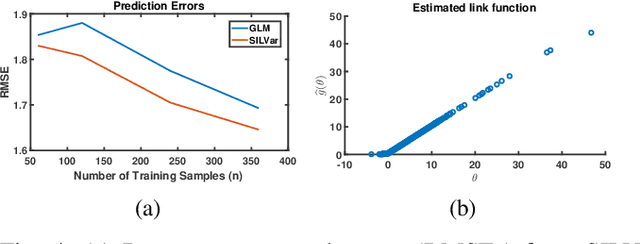
A semi-parametric, non-linear regression model in the presence of latent variables is introduced. These latent variables can correspond to unmodeled phenomena or unmeasured agents in a complex networked system. This new formulation allows joint estimation of certain non-linearities in the system, the direct interactions between measured variables, and the effects of unmodeled elements on the observed system. The particular form of the model adopted is justified, and learning is posed as a regularized empirical risk minimization. This leads to classes of structured convex optimization problems with a "sparse plus low-rank" flavor. Relations between the proposed model and several common model paradigms, such as those of Robust Principal Component Analysis (PCA) and Vector Autoregression (VAR), are established. Particularly in the VAR setting, the low-rank contributions can come from broad trends exhibited in the time series. Details of the algorithm for learning the model are presented. Experiments demonstrate the performance of the model and the estimation algorithm on simulated and real data.

Signal Processing on Graphs: Causal Modeling of Unstructured Data

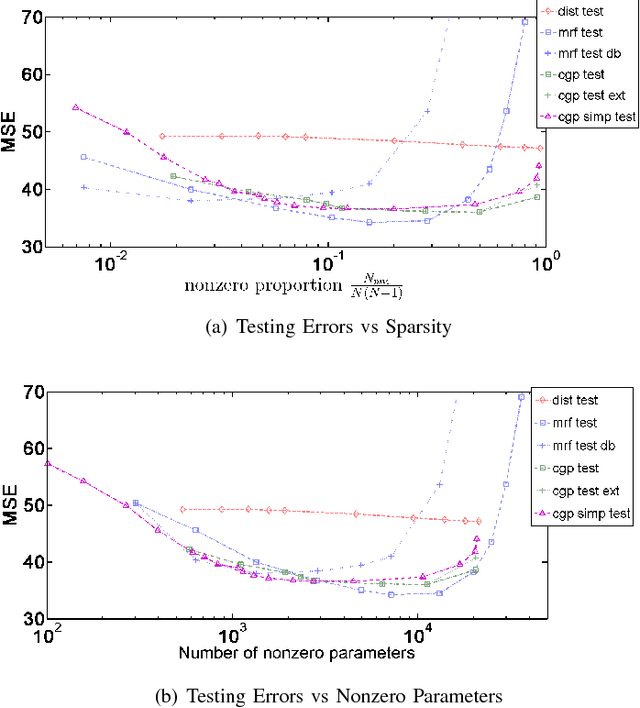
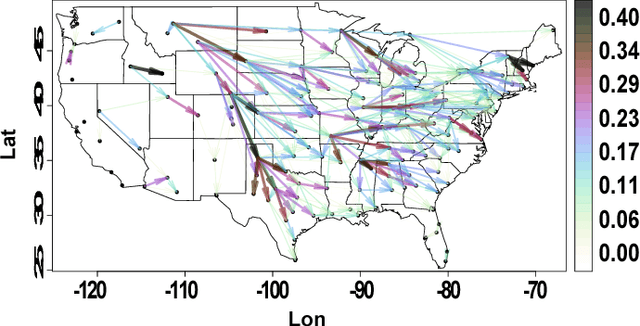
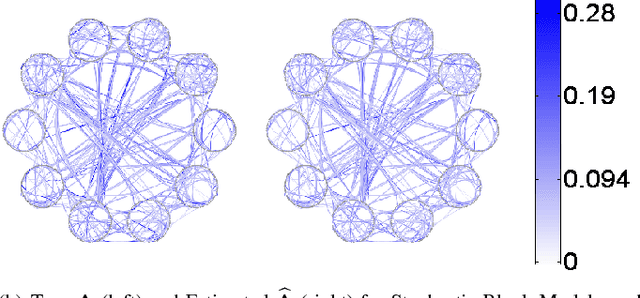
Many applications collect a large number of time series, for example, the financial data of companies quoted in a stock exchange, the health care data of all patients that visit the emergency room of a hospital, or the temperature sequences continuously measured by weather stations across the US. These data are often referred to as unstructured. A first task in its analytics is to derive a low dimensional representation, a graph or discrete manifold, that describes well the interrelations among the time series and their intrarelations across time. This paper presents a computationally tractable algorithm for estimating this graph that structures the data. The resulting graph is directed and weighted, possibly capturing causal relations, not just reciprocal correlations as in many existing approaches in the literature. A convergence analysis is carried out. The algorithm is demonstrated on random graph datasets and real network time series datasets, and its performance is compared to that of related methods. The adjacency matrices estimated with the new method are close to the true graph in the simulated data and consistent with prior physical knowledge in the real dataset tested.