A Neuro-Symbolic Approach to Multi-Agent RL for Interpretability and Probabilistic Decision Making

Multi-agent reinforcement learning (MARL) is well-suited for runtime decision-making in optimizing the performance of systems where multiple agents coexist and compete for shared resources. However, applying common deep learning-based MARL solutions to real-world problems suffers from issues of interpretability, sample efficiency, partial observability, etc. To address these challenges, we present an event-driven formulation, where decision-making is handled by distributed co-operative MARL agents using neuro-symbolic methods. The recently introduced neuro-symbolic Logical Neural Networks (LNN) framework serves as a function approximator for the RL, to train a rules-based policy that is both logical and interpretable by construction. To enable decision-making under uncertainty and partial observability, we developed a novel probabilistic neuro-symbolic framework, Probabilistic Logical Neural Networks (PLNN), which combines the capabilities of logical reasoning with probabilistic graphical models. In PLNN, the upward/downward inference strategy, inherited from LNN, is coupled with belief bounds by setting the activation function for the logical operator associated with each neural network node to a probability-respecting generalization of the Fr\'echet inequalities. These PLNN nodes form the unifying element that combines probabilistic logic and Bayes Nets, permitting inference for variables with unobserved states. We demonstrate our contributions by addressing key MARL challenges for power sharing in a system-on-chip application.

E-PDDL: A Standardized Way of Defining Epistemic Planning Problems

Epistemic Planning (EP) refers to an automated planning setting where the agent reasons in the space of knowledge states and tries to find a plan to reach a desirable state from the current state. Its general form, the Multi-agent Epistemic Planning (MEP) problem involves multiple agents who need to reason about both the state of the world and the information flow between agents. In a MEP problem, multiple approaches have been developed recently with varying restrictions, such as considering only the concept of knowledge while not allowing the idea of belief, or not allowing for ``complex" modal operators such as those needed to handle dynamic common knowledge. While the diversity of approaches has led to a deeper understanding of the problem space, the lack of a standardized way to specify MEP problems independently of solution approaches has created difficulties in comparing performance of planners, identifying promising techniques, exploring new strategies like ensemble methods, and making it easy for new researchers to contribute to this research area. To address the situation, we propose a unified way of specifying EP problems - the Epistemic Planning Domain Definition Language, E-PDDL. We show that E-PPDL can be supported by leading MEP planners and provide corresponding parser code that translates EP problems specified in E-PDDL into (M)EP problems that can be handled by several planners. This work is also useful in building more general epistemic planning environments where we envision a meta-cognitive module that takes a planning problem in E-PDDL, identifies and assesses some of its features, and autonomously decides which planner is the best one to solve it.

A Finitist's Manifesto: Do we need to Reformulate the Foundations of Mathematics?

There is a problem with the foundations of classical mathematics, and potentially even with the foundations of computer science, that mathematicians have by-and-large ignored. This essay is a call for practicing mathematicians who have been sleep-walking in their infinitary mathematical paradise to take heed. Much of mathematics relies upon either (i) the "existence'" of objects that contain an infinite number of elements, (ii) our ability, "in theory", to compute with an arbitrary level of precision, or (iii) our ability, "in theory", to compute for an arbitrarily large number of time steps. All of calculus relies on the notion of a limit. The monumental results of real and complex analysis rely on a seamless notion of the "continuum" of real numbers, which extends in the plane to the complex numbers and gives us, among other things, "rigorous" definitions of continuity, the derivative, various different integrals, as well as the fundamental theorems of calculus and of algebra -- the former of which says that the derivative and integral can be viewed as inverse operations, and the latter of which says that every polynomial over $\mathbb{C}$ has a complex root. This essay is an inquiry into whether there is any way to assign meaning to the notions of "existence" and "in theory'" in (i) to (iii) above.

Analysis of Watson's Strategies for Playing Jeopardy!

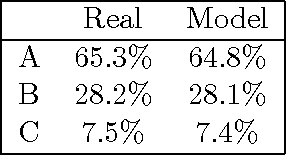
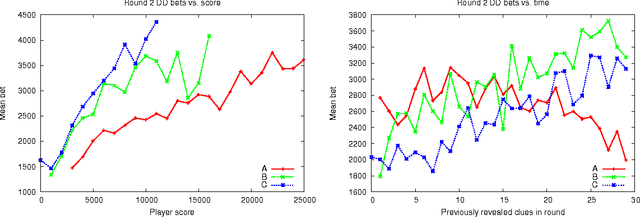
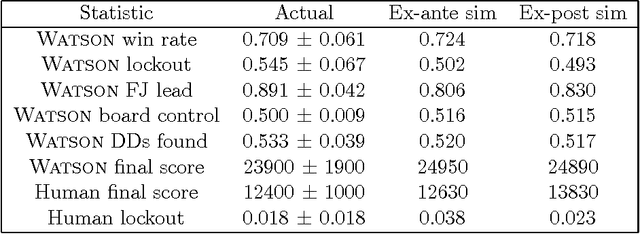
Major advances in Question Answering technology were needed for IBM Watson to play Jeopardy! at championship level -- the show requires rapid-fire answers to challenging natural language questions, broad general knowledge, high precision, and accurate confidence estimates. In addition, Jeopardy! features four types of decision making carrying great strategic importance: (1) Daily Double wagering; (2) Final Jeopardy wagering; (3) selecting the next square when in control of the board; (4) deciding whether to attempt to answer, i.e., "buzz in." Using sophisticated strategies for these decisions, that properly account for the game state and future event probabilities, can significantly boost a players overall chances to win, when compared with simple "rule of thumb" strategies. This article presents our approach to developing Watsons game-playing strategies, comprising development of a faithful simulation model, and then using learning and Monte-Carlo methods within the simulator to optimize Watsons strategic decision-making. After giving a detailed description of each of our game-strategy algorithms, we then focus in particular on validating the accuracy of the simulators predictions, and documenting performance improvements using our methods. Quantitative performance benefits are shown with respect to both simple heuristic strategies, and actual human contestant performance in historical episodes. We further extend our analysis of human play to derive a number of valuable and counterintuitive examples illustrating how human contestants may improve their performance on the show.