Spline Dimensional Decomposition with Interpolation-based Optimal Knot Selection for Stochastic Dynamic Analysis

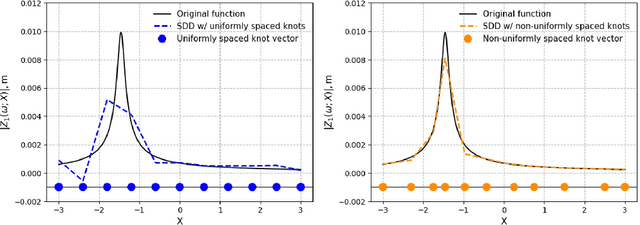
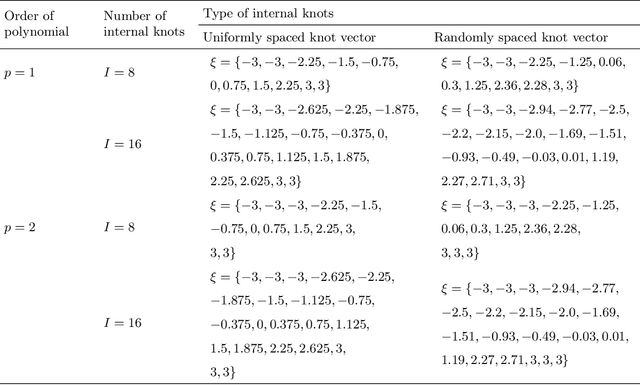
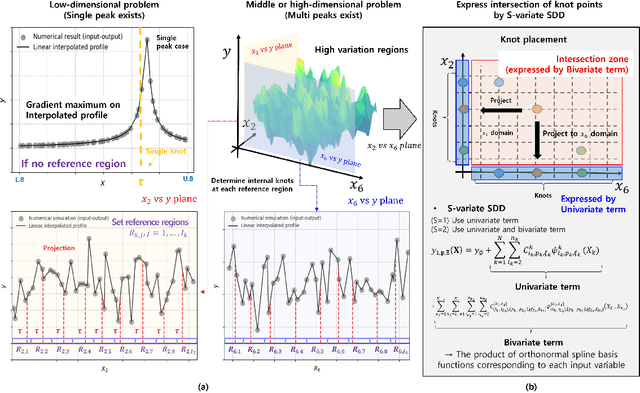
Forward uncertainty quantification in dynamic systems is challenging due to non-smooth or locally oscillating nonlinear behaviors. Spline dimensional decomposition (SDD) effectively addresses such nonlinearity by partitioning input coordinates via knot placement, yet its accuracy is highly sensitive to the location of internal knots. Optimizing knots through sequential quadratic programming can be effective, yet the optimization process becomes computationally intense. We propose a computationally efficient, interpolation-based method for optimal knot selection in SDD. The method involves three steps: (1) interpolating input-output profiles, (2) defining subinterval-based reference regions, and (3) selecting optimal knot locations at maximum gradient points within each region. The resulting knot vector is then applied to SDD for accurate approximation of non-smooth and locally oscillating responses. A modal analysis of a lower control arm demonstrates that SDD with the proposed knot selection achieves higher accuracy than SDD with uniformly or randomly spaced knots, and also a Gaussian process surrogate model. The proposed SDD exhibits the lowest relative variance error (2.89%), compared to SDD with uniformly spaced knots (12.310%), randomly spaced knots (15.274%), and Gaussian process (5.319%) in the first natural frequency distribution. All surrogate models are constructed using the same 401 simulation datasets, and the relative errors are evaluated against a 2000-sample Monte Carlo simulation. The scalability and applicability of proposed method are demonstrated through stochastic and reliability analyses of mathematical functions (N=1, 3) and a lower control arm system (N=10). The results confirm that both second-moment statistics and reliability estimates can be accurately achieved with only a few hundred function evaluations or finite element simulations.

SMT 2.0: A Surrogate Modeling Toolbox with a focus on Hierarchical and Mixed Variables Gaussian Processes

The Surrogate Modeling Toolbox (SMT) is an open-source Python package that offers a collection of surrogate modeling methods, sampling techniques, and a set of sample problems. This paper presents SMT 2.0, a major new release of SMT that introduces significant upgrades and new features to the toolbox. This release adds the capability to handle mixed-variable surrogate models and hierarchical variables. These types of variables are becoming increasingly important in several surrogate modeling applications. SMT 2.0 also improves SMT by extending sampling methods, adding new surrogate models, and computing variance and kernel derivatives for Kriging. This release also includes new functions to handle noisy and use multifidelity data. To the best of our knowledge, SMT 2.0 is the first open-source surrogate library to propose surrogate models for hierarchical and mixed inputs. This open-source software is distributed under the New BSD license.