John K. Golden
Learning to regularize with a variational autoencoder for hydrologic inverse analysis
Jun 06, 2019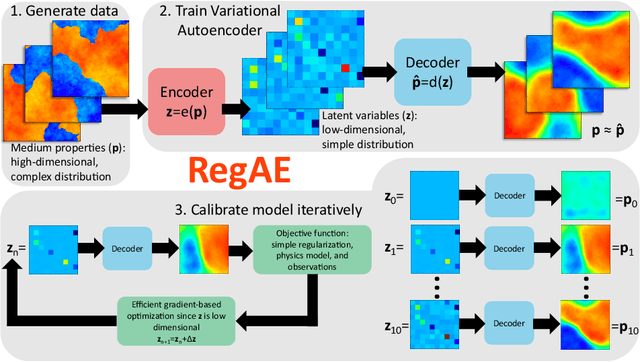
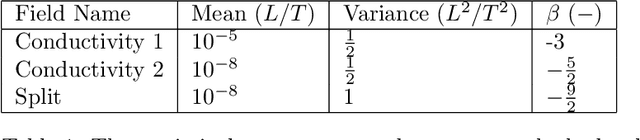
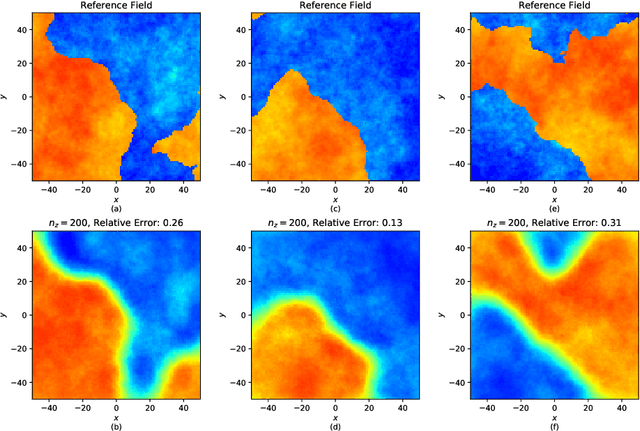
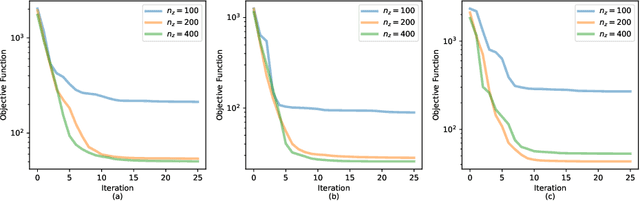
Abstract:Inverse problems often involve matching observational data using a physical model that takes a large number of parameters as input. These problems tend to be under-constrained and require regularization to impose additional structure on the solution in parameter space. A central difficulty in regularization is turning a complex conceptual model of this additional structure into a functional mathematical form to be used in the inverse analysis. In this work we propose a method of regularization involving a machine learning technique known as a variational autoencoder (VAE). The VAE is trained to map a low-dimensional set of latent variables with a simple structure to the high-dimensional parameter space that has a complex structure. We train a VAE on unconditioned realizations of the parameters for a hydrological inverse problem. These unconditioned realizations neither rely on the observational data used to perform the inverse analysis nor require any forward runs of the physical model, thus making the computational cost of generating the training data minimal. The central benefit of this approach is that regularization is then performed on the latent variables from the VAE, which can be regularized simply. A second benefit of this approach is that the VAE reduces the number of variables in the optimization problem, thus making gradient-based optimization more computationally efficient when adjoint methods are unavailable. After performing regularization and optimization on the latent variables, the VAE then decodes the problem back to the original parameter space. Our approach constitutes a novel framework for regularization and optimization, readily applicable to a wide range of inverse problems. We call the approach RegAE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge