Provable Low Rank Plus Sparse Matrix Separation Via Nonconvex Regularizers

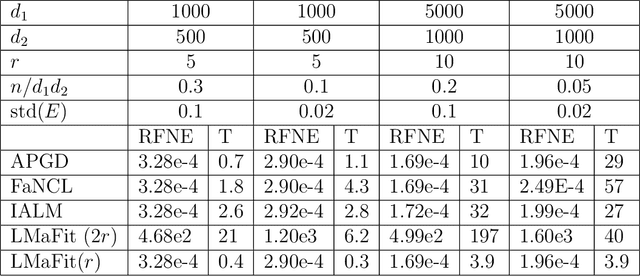
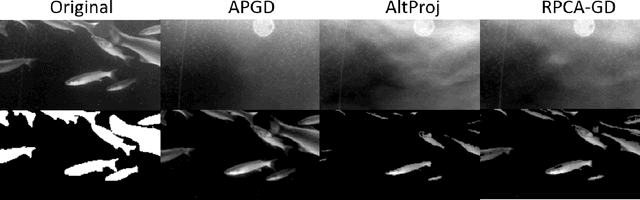
This paper considers a large class of problems where we seek to recover a low rank matrix and/or sparse vector from some set of measurements. While methods based on convex relaxations suffer from a (possibly large) estimator bias, and other nonconvex methods require the rank or sparsity to be known a priori, we use nonconvex regularizers to minimize the rank and $l_0$ norm without the estimator bias from the convex relaxation. We present a novel analysis of the alternating proximal gradient descent algorithm applied to such problems, and bound the error between the iterates and the ground truth sparse and low rank matrices. The algorithm and error bound can be applied to sparse optimization, matrix completion, and robust principal component analysis as special cases of our results.

Training Deep Neural Networks with Constrained Learning Parameters

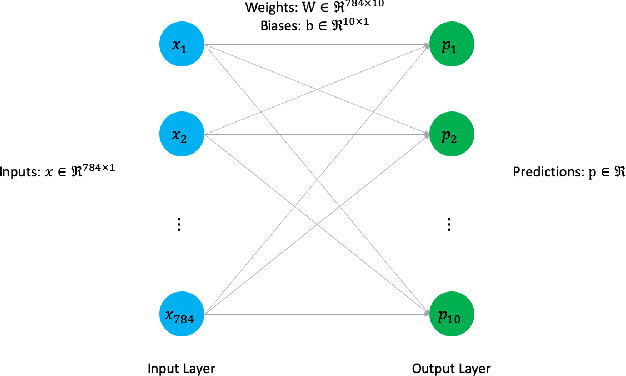
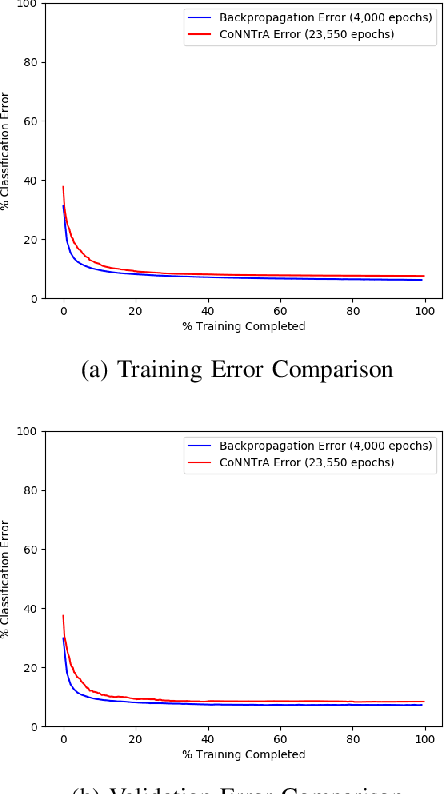
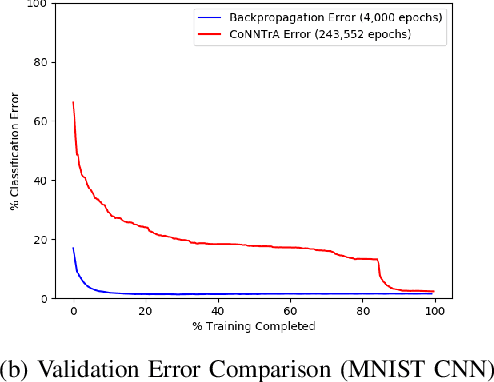
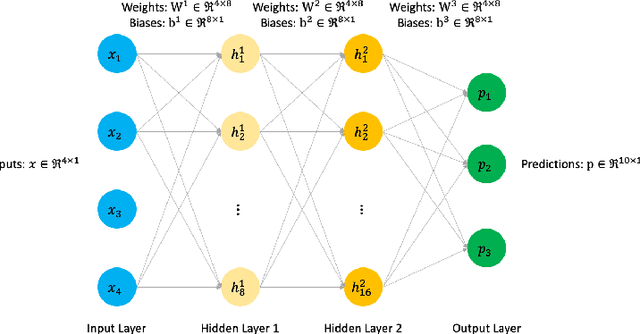
Today's deep learning models are primarily trained on CPUs and GPUs. Although these models tend to have low error, they consume high power and utilize large amount of memory owing to double precision floating point learning parameters. Beyond the Moore's law, a significant portion of deep learning tasks would run on edge computing systems, which will form an indispensable part of the entire computation fabric. Subsequently, training deep learning models for such systems will have to be tailored and adopted to generate models that have the following desirable characteristics: low error, low memory, and low power. We believe that deep neural networks (DNNs), where learning parameters are constrained to have a set of finite discrete values, running on neuromorphic computing systems would be instrumental for intelligent edge computing systems having these desirable characteristics. To this extent, we propose the Combinatorial Neural Network Training Algorithm (CoNNTrA), that leverages a coordinate gradient descent-based approach for training deep learning models with finite discrete learning parameters. Next, we elaborate on the theoretical underpinnings and evaluate the computational complexity of CoNNTrA. As a proof of concept, we use CoNNTrA to train deep learning models with ternary learning parameters on the MNIST, Iris and ImageNet data sets and compare their performance to the same models trained using Backpropagation. We use following performance metrics for the comparison: (i) Training error; (ii) Validation error; (iii) Memory usage; and (iv) Training time. Our results indicate that CoNNTrA models use 32x less memory and have errors at par with the Backpropagation models.

Low-Rank Factorization for Rank Minimization with Nonconvex Regularizers

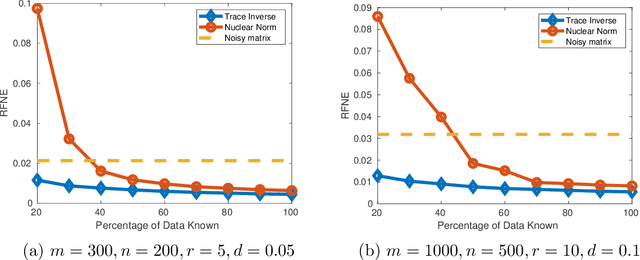
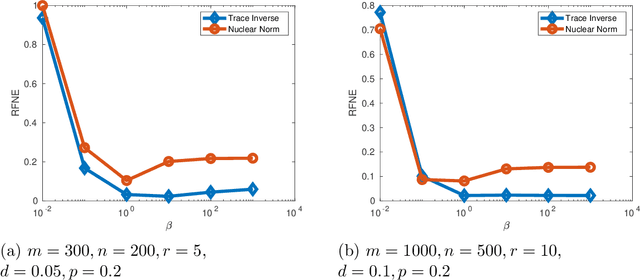
Rank minimization is of interest in machine learning applications such as recommender systems and robust principal component analysis. Minimizing the convex relaxation to the rank minimization problem, the nuclear norm, is an effective technique to solve the problem with strong performance guarantees. However, nonconvex relaxations have less estimation bias than the nuclear norm and can more accurately reduce the effect of noise on the measurements. We develop efficient algorithms based on iteratively reweighted nuclear norm schemes, while also utilizing the low rank factorization for semidefinite programs put forth by Burer and Monteiro. We prove convergence and computationally show the advantages over convex relaxations and alternating minimization methods. Additionally, the computational complexity of each iteration of our algorithm is on par with other state of the art algorithms, allowing us to quickly find solutions to the rank minimization problem for large matrices.