LFFR: Logistic Function For (single-output) Regression

Privacy-preserving regression in machine learning is a crucial area of research, aimed at enabling the use of powerful machine learning techniques while protecting individuals' privacy. In this paper, we implement privacy-preserving regression training using data encrypted under a fully homomorphic encryption scheme. We first examine the common linear regression algorithm and propose a (simplified) fixed Hessian for linear regression training, which can be applied for any datasets even not normalized into the range $[0, 1]$. We also generalize this constant Hessian matrix to the ridge regression version, namely linear regression which includes a regularization term to penalize large coefficients. However, our main contribution is to develop a novel and efficient algorithm called LFFR for homomorphic regression using the logistic function, which could model more complex relations between input values and output prediction in comparison with linear regression. We also find a constant simplified Hessian to train our LFFR algorithm using the Newton-like method and compare it against to with our new fixed Hessian linear regression training over two real-world datasets. We suggest normalizing not only the data but also the target predictions even for the original linear regression used in a privacy-preserving manner, which is helpful to remain weights in a small range, say $[-5, +5]$ good for refreshing ciphertext setting parameters, and avoid tuning the regularization parameter $\lambda$ via cross validation. The linear regression with normalized predictions could be a viable alternative to ridge regression.

Privacy-Preserving 3-Layer Neural Network Training using Mere Homomorphic Encryption Technique

In this manuscript, we consider the problem of privacy-preserving training of neural networks in the mere homomorphic encryption setting. We combine several exsiting techniques available, extend some of them, and finally enable the training of 3-layer neural networks for both the regression and classification problems using mere homomorphic encryption technique.

Activation Functions Not To Active: A Plausible Theory on Interpreting Neural Networks

Researchers commonly believe that neural networks model a high-dimensional space but cannot give a clear definition of this space. What is this space? What is its dimension? And does it has finite dimensions? In this paper, we develop a plausible theory on interpreting neural networks in terms of the role of activation functions in neural networks and define a high-dimensional (more precisely, an infinite-dimensional) space that neural networks including deep-learning networks could create. We show that the activation function acts as a magnifying function that maps the low-dimensional linear space into an infinite-dimensional space, which can distinctly identify the polynomial approximation of any multivariate continuous function of the variable values being the same features of the given dataset. Given a dataset with each example of $d$ features $f_1$, $f_2$, $\cdots$, $f_d$, we believe that neural networks model a special space with infinite dimensions, each of which is a monomial $$\prod_{i_1, i_2, \cdots, i_d} f_1^{i_1} f_2^{i_2} \cdots f_d^{i_d}$$ for some non-negative integers ${i_1, i_2, \cdots, i_d} \in \mathbb{Z}_{0}^{+}=\{0,1,2,3,\ldots\} $. We term such an infinite-dimensional space a $\textit{ Super Space (SS)}$. We see such a dimension as the minimum information unit. Every neuron node previously through an activation layer in neural networks is a $\textit{ Super Plane (SP) }$, which is actually a polynomial of infinite degree. This $\textit{ Super Space }$ is something like a coordinate system, in which every multivalue function can be represented by a $\textit{ Super Plane }$. We also show that training NNs could at least be reduced to solving a system of nonlinear equations. %solve sets of nonlinear equations

Privacy-Preserving CNN Training with Transfer Learning

Privacy-preserving nerual network inference has been well studied while homomorphic CNN training still remains an open challenging task. In this paper, we present a practical solution to implement privacy-preserving CNN training based on mere Homomorphic Encryption (HE) technique. To our best knowledge, this is the first attempt successfully to crack this nut and no work ever before has achieved this goal. Several techniques combine to make it done: (1) with transfer learning, privacy-preserving CNN training can be reduced to homomorphic neural network training, or even multiclass logistic regression (MLR) training; (2) via a faster gradient variant called $\texttt{Quadratic Gradient}$, an enhanced gradient method for MLR with a state-of-the-art performance in converge speed is applied in this work to achieve high performance; (3) we employ the thought of transformation in mathematics to transform approximating Softmax function in encryption domain to the well-studied approximation of Sigmoid function. A new type of loss function is alongside been developed to complement this change; and (4) we use a simple but flexible matrix-encoding method named $\texttt{Volley Revolver}$ to manage the data flow in the ciphertexts, which is the key factor to complete the whole homomorphic CNN training. The complete, runnable C++ code to implement our work can be found at: https://github.com/petitioner/HE.CNNtraining. We select $\texttt{REGNET\_X\_400MF}$ as our pre-train model for using transfer learning. We use the first 128 MNIST training images as training data and the whole MNIST testing dataset as the testing data. The client only needs to upload 6 ciphertexts to the cloud and it takes $\sim 21$ mins to perform 2 iterations on a cloud with 64 vCPUs, resulting in a precision of $21.49\%$.

Quadratic Gradient: Uniting Gradient Algorithm and Newton Method as One

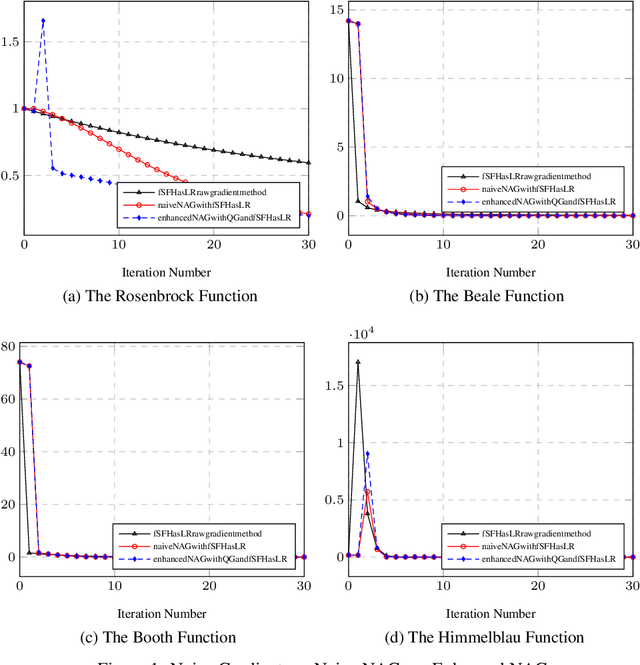
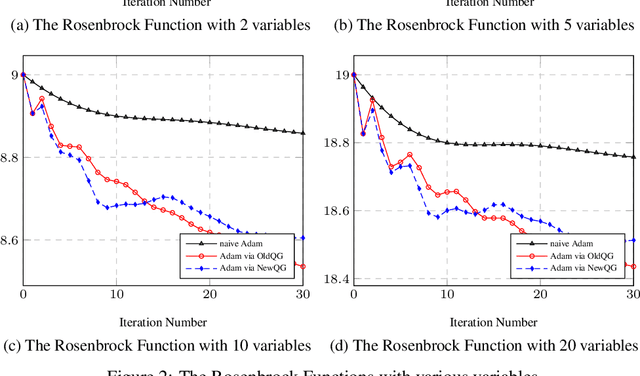
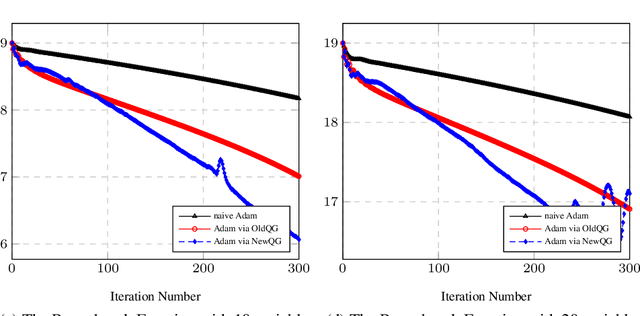
It might be inadequate for the line search technique for Newton's method to use only one floating point number. A column vector of the same size as the gradient might be better than a mere float number to accelerate each of the gradient elements with different rates. Moreover, a square matrix of the same order as the Hessian matrix might be helpful to correct the Hessian matrix. Chiang applied something between a column vector and a square matrix, namely a diagonal matrix, to accelerate the gradient and further proposed a faster gradient variant called quadratic gradient. In this paper, we present a new way to build a new version of the quadratic gradient. This new quadratic gradient doesn't satisfy the convergence conditions of the fixed Hessian Newton's method. However, experimental results show that it sometimes has a better performance than the original one in convergence rate. Also, Chiang speculates that there might be a relation between the Hessian matrix and the learning rate for the first-order gradient descent method. We prove that the floating number $\frac{1}{\epsilon + \max \{| \lambda_i | \}}$ can be a good learning rate of the gradient methods, where $\epsilon$ is a number to avoid division by zero and $\lambda_i$ the eigenvalues of the Hessian matrix.

Multinomial Logistic Regression Algorithms via Quadratic Gradient

Multinomial logistic regression, also known by other names such as multiclass logistic regression and softmax regression, is a fundamental classification method that generalizes binary logistic regression to multiclass problems. A recently work proposed a faster gradient called $\texttt{quadratic gradient}$ that can accelerate the binary logistic regression training, and presented an enhanced Nesterov's accelerated gradient (NAG) method for binary logistic regression. In this paper, we extend this work to multiclass logistic regression and propose an enhanced Adaptive Gradient Algorithm (Adagrad) that can accelerate the original Adagrad method. We test the enhanced NAG method and the enhanced Adagrad method on some multiclass-problem datasets. Experimental results show that both enhanced methods converge faster than their original ones respectively.

On Polynomial Approximation of Activation Function

In this work, we propose an interesting method that aims to approximate an activation function over some domain by polynomials of the presupposing low degree. The main idea behind this method can be seen as an extension of the ordinary least square method and includes the gradient of activation function into the cost function to minimize.

A Novel Matrix-Encoding Method for Privacy-Preserving Neural Networks

In this work, we present $\texttt{Volley Revolver}$, a novel matrix-encoding method that is particularly convenient for privacy-preserving neural networks to make predictions, and use it to implement a CNN for handwritten image classification. Based on this encoding method, we develop several additional operations for putting into practice the secure matrix multiplication over encrypted data matrices. For two matrices $A$ and $B$ to perform multiplication $A \times B$, the main idea is, in a simple version, to encrypt matrix $A$ and the transposition of the matrix $B$ into two ciphertexts respectively. Along with the additional operations, the homomorphic matrix multiplication $A \times B$ can be calculated over encrypted data matrices efficiently. For the convolution operation in CNN, on the basis of the $\texttt{Volley Revolver}$ encoding method, we develop a feasible and efficient evaluation strategy for performing the convolution operation. We in advance span each convolution kernel of CNN to a matrix space of the same size as the input image so as to generate several ciphertexts, each of which is later used together with the input image for calculating some part of the final convolution result. We accumulate all these part results of convolution operation and thus obtain the final convolution result.

Privacy-Preserving Logistic Regression Training with a Faster Gradient Variant

Logistic regression training on an encrypted dataset has been an attractive idea to security concerns for years. In this paper, we propose a faster gradient variant called Quadratic Gradient for logistic regression and implement it via a special homomorphic encryption scheme. The core of this gradient variant can be seen as an extension of the simplified fixed Hessian from Newton's method, which extracts information from the Hessian matrix into the naive gradient, and thus can be used to enhance Nesterov's accelerated gradient (NAG), Adagrad, etc. We evaluate various gradient $ascent$ methods with this gradient variant on the gene dataset provided by the 2017 iDASH competition and the image dataset from the MNIST database. Experimental results show that the enhanced methods converge faster and sometimes even to a better convergence result. We also implement the gradient variant in full batch NAG and mini-batch NAG for training a logistic regression model on a large dataset in the encrypted domain. Equipped with this gradient variant, full batch NAG and mini-batch NAG are both faster than the original ones.