Vector Field Neural Networks

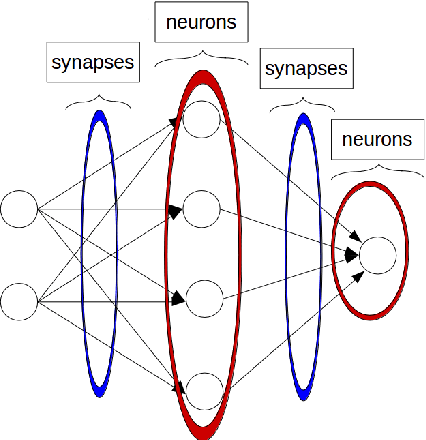
This work begins by establishing a mathematical formalization between different geometrical interpretations of Neural Networks, providing a first contribution. From this starting point, a new interpretation is explored, using the idea of implicit vector fields moving data as particles in a flow. A new architecture, Vector Fields Neural Networks(VFNN), is proposed based on this interpretation, with the vector field becoming explicit. A specific implementation of the VFNN using Euler's method to solve ordinary differential equations (ODEs) and gaussian vector fields is tested. The first experiments present visual results remarking the important features of the new architecture and providing another contribution with the geometrically interpretable regularization of model parameters. Then, the new architecture is evaluated for different hyperparameters and inputs, with the objective of evaluating the influence on model performance, computational time, and complexity. The VFNN model is compared against the known basic models Naive Bayes, Feed Forward Neural Networks, and Support Vector Machines(SVM), showing comparable, or better, results for different datasets. Finally, the conclusion provides many new questions and ideas for improvement of the model that can be used to increase model performance.

Vector Field Based Neural Networks

A novel Neural Network architecture is proposed using the mathematically and physically rich idea of vector fields as hidden layers to perform nonlinear transformations in the data. The data points are interpreted as particles moving along a flow defined by the vector field which intuitively represents the desired movement to enable classification. The architecture moves the data points from their original configuration to anew one following the streamlines of the vector field with the objective of achieving a final configuration where classes are separable. An optimization problem is solved through gradient descent to learn this vector field.