On Conditional Independence Graph Learning From Multi-Attribute Gaussian Dependent Time Series

Estimation of the conditional independence graph (CIG) of high-dimensional multivariate Gaussian time series from multi-attribute data is considered. Existing methods for graph estimation for such data are based on single-attribute models where one associates a scalar time series with each node. In multi-attribute graphical models, each node represents a random vector or vector time series. In this paper we provide a unified theoretical analysis of multi-attribute graph learning for dependent time series using a penalized log-likelihood objective function formulated in the frequency domain using the discrete Fourier transform of the time-domain data. We consider both convex (sparse-group lasso) and non-convex (log-sum and SCAD group penalties) penalty/regularization functions. We establish sufficient conditions in a high-dimensional setting for consistency (convergence of the inverse power spectral density to true value in the Frobenius norm), local convexity when using non-convex penalties, and graph recovery. We do not impose any incoherence or irrepresentability condition for our convergence results. We also empirically investigate selection of the tuning parameters based on the Bayesian information criterion, and illustrate our approach using numerical examples utilizing both synthetic and real data.

Sparse Graph Learning Under Laplacian-Related Constraints

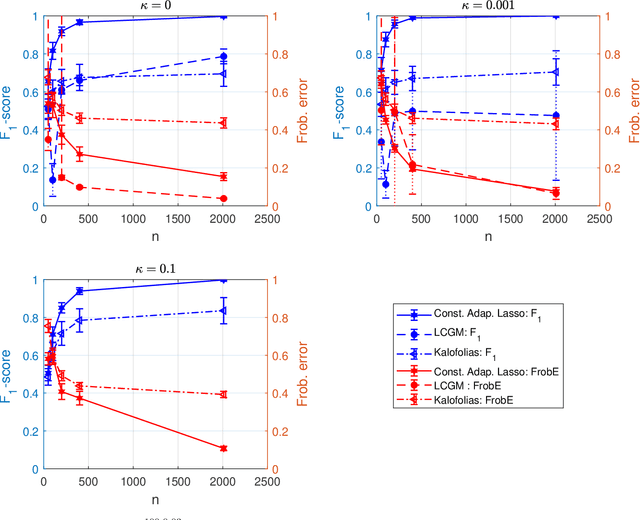
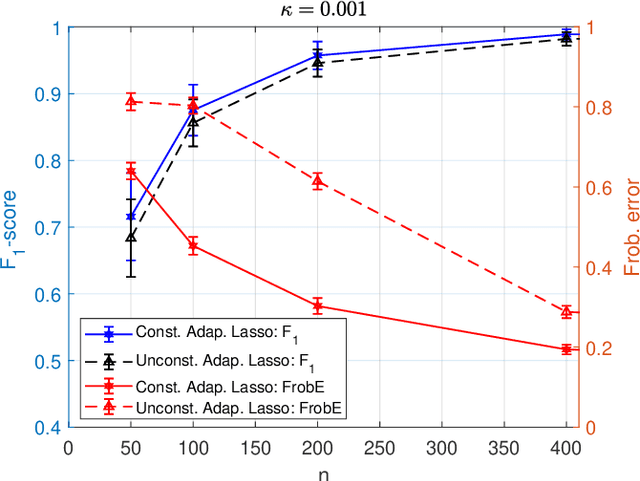
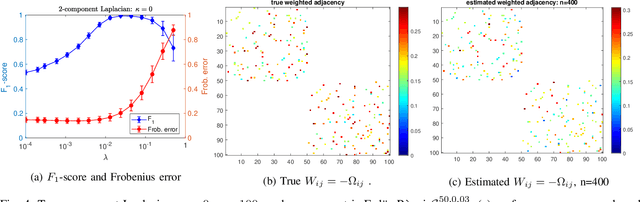
We consider the problem of learning a sparse undirected graph underlying a given set of multivariate data. We focus on graph Laplacian-related constraints on the sparse precision matrix that encodes conditional dependence between the random variables associated with the graph nodes. Under these constraints the off-diagonal elements of the precision matrix are non-positive (total positivity), and the precision matrix may not be full-rank. We investigate modifications to widely used penalized log-likelihood approaches to enforce total positivity but not the Laplacian structure. The graph Laplacian can then be extracted from the off-diagonal precision matrix. An alternating direction method of multipliers (ADMM) algorithm is presented and analyzed for constrained optimization under Laplacian-related constraints and lasso as well as adaptive lasso penalties. Numerical results based on synthetic data show that the proposed constrained adaptive lasso approach significantly outperforms existing Laplacian-based approaches. We also evaluate our approach on real financial data.

On Sparse High-Dimensional Graphical Model Learning For Dependent Time Series

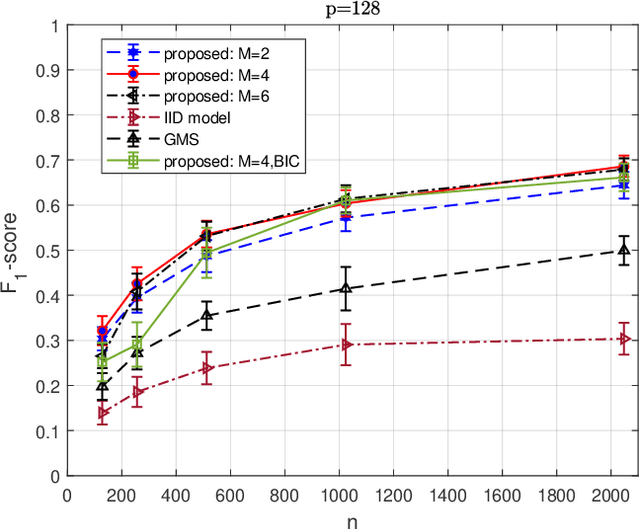
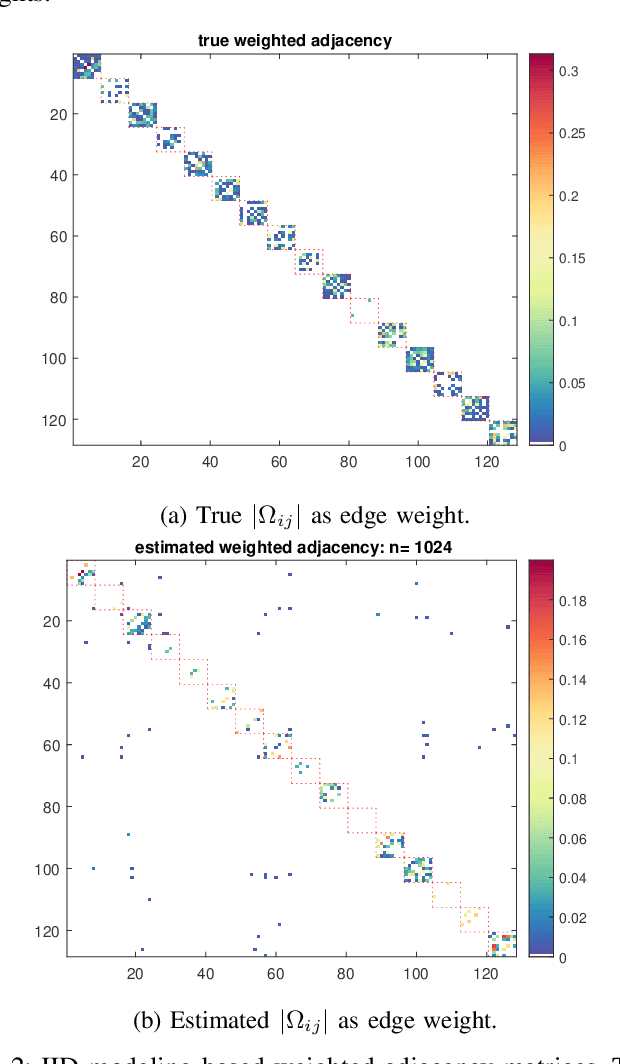
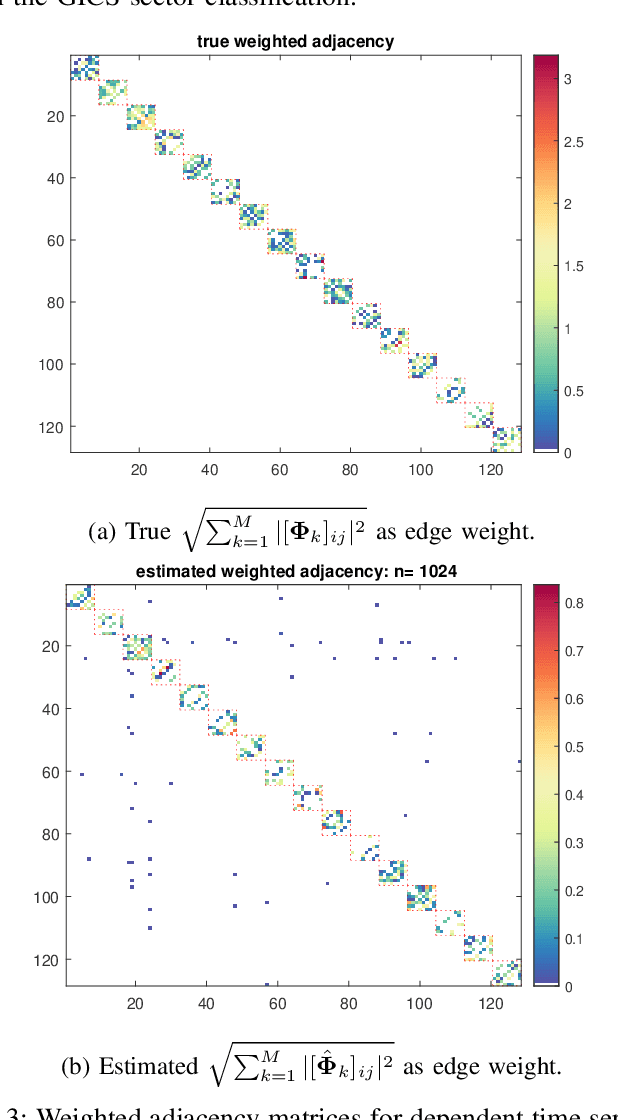
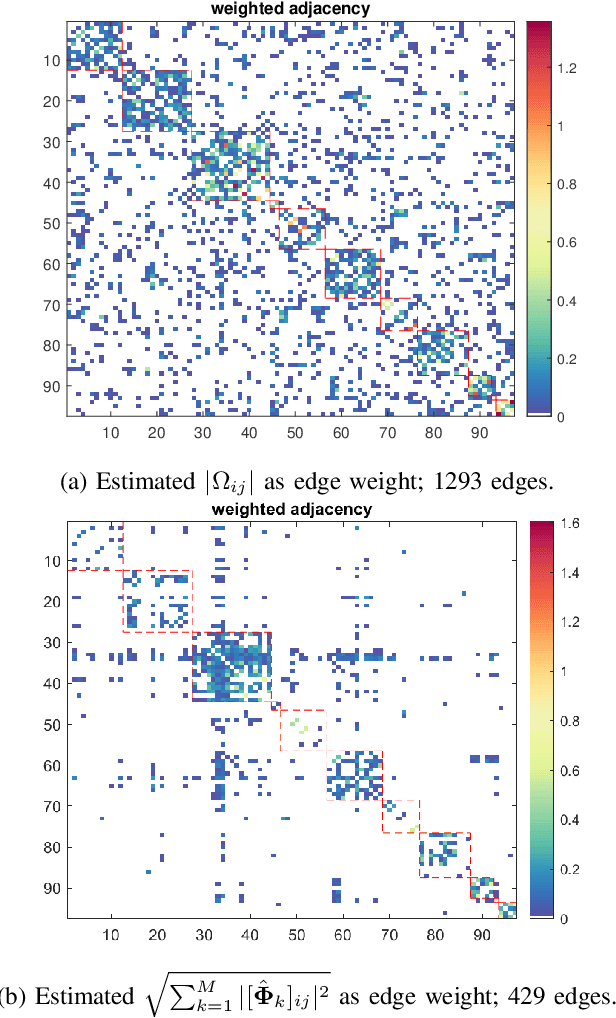
We consider the problem of inferring the conditional independence graph (CIG) of a sparse, high-dimensional stationary multivariate Gaussian time series. A sparse-group lasso-based frequency-domain formulation of the problem based on frequency-domain sufficient statistic for the observed time series is presented. We investigate an alternating direction method of multipliers (ADMM) approach for optimization of the sparse-group lasso penalized log-likelihood. We provide sufficient conditions for convergence in the Frobenius norm of the inverse PSD estimators to the true value, jointly across all frequencies, where the number of frequencies are allowed to increase with sample size. This results also yields a rate of convergence. We also empirically investigate selection of the tuning parameters based on Bayesian information criterion, and illustrate our approach using numerical examples utilizing both synthetic and real data.