Expressive Score-Based Priors for Distribution Matching with Geometry-Preserving Regularization

Distribution matching (DM) is a versatile domain-invariant representation learning technique that has been applied to tasks such as fair classification, domain adaptation, and domain translation. Non-parametric DM methods struggle with scalability and adversarial DM approaches suffer from instability and mode collapse. While likelihood-based methods are a promising alternative, they often impose unnecessary biases through fixed priors or require explicit density models (e.g., flows) that can be challenging to train. We address this limitation by introducing a novel approach to training likelihood-based DM using expressive score-based prior distributions. Our key insight is that gradient-based DM training only requires the prior's score function -- not its density -- allowing us to train the prior via denoising score matching. This approach eliminates biases from fixed priors (e.g., in VAEs), enabling more effective use of geometry-preserving regularization, while avoiding the challenge of learning an explicit prior density model (e.g., a flow-based prior). Our method also demonstrates better stability and computational efficiency compared to other diffusion-based priors (e.g., LSGM). Furthermore, experiments demonstrate superior performance across multiple tasks, establishing our score-based method as a stable and effective approach to distribution matching. Source code available at https://github.com/inouye-lab/SAUB.

Discrete Tree Flows via Tree-Structured Permutations

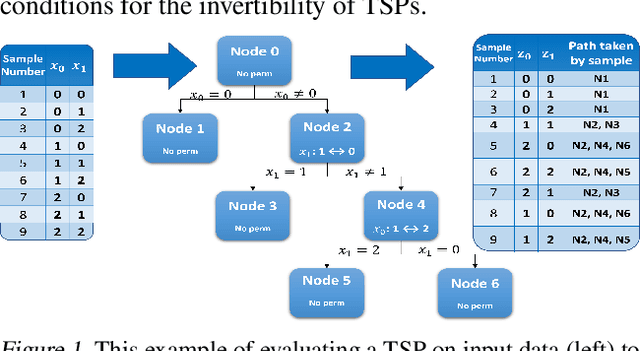
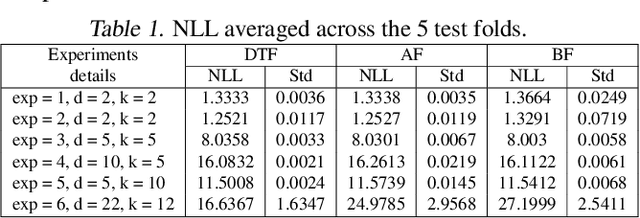
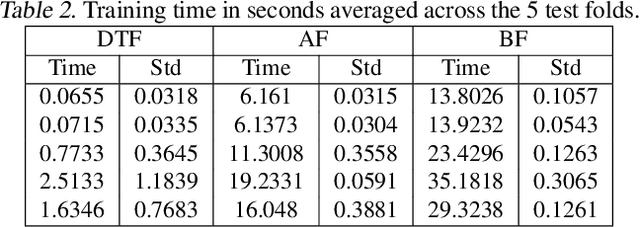
While normalizing flows for continuous data have been extensively researched, flows for discrete data have only recently been explored. These prior models, however, suffer from limitations that are distinct from those of continuous flows. Most notably, discrete flow-based models cannot be straightforwardly optimized with conventional deep learning methods because gradients of discrete functions are undefined or zero. Previous works approximate pseudo-gradients of the discrete functions but do not solve the problem on a fundamental level. In addition to that, backpropagation can be computationally burdensome compared to alternative discrete algorithms such as decision tree algorithms. Our approach seeks to reduce computational burden and remove the need for pseudo-gradients by developing a discrete flow based on decision trees -- building upon the success of efficient tree-based methods for classification and regression for discrete data. We first define a tree-structured permutation (TSP) that compactly encodes a permutation of discrete data where the inverse is easy to compute; thus, we can efficiently compute the density value and sample new data. We then propose a decision tree algorithm to build TSPs that learns the tree structure and permutations at each node via novel criteria. We empirically demonstrate the feasibility of our method on multiple datasets.