uniINF: Best-of-Both-Worlds Algorithm for Parameter-Free Heavy-Tailed MABs

In this paper, we present a novel algorithm, uniINF, for the Heavy-Tailed Multi-Armed Bandits (HTMAB) problem, demonstrating robustness and adaptability in both stochastic and adversarial environments. Unlike the stochastic MAB setting where loss distributions are stationary with time, our study extends to the adversarial setup, where losses are generated from heavy-tailed distributions that depend on both arms and time. Our novel algorithm `uniINF` enjoys the so-called Best-of-Both-Worlds (BoBW) property, performing optimally in both stochastic and adversarial environments without knowing the exact environment type. Moreover, our algorithm also possesses a Parameter-Free feature, i.e., it operates without the need of knowing the heavy-tail parameters $(\sigma, \alpha)$ a-priori. To be precise, uniINF ensures nearly-optimal regret in both stochastic and adversarial environments, matching the corresponding lower bounds when $(\sigma, \alpha)$ is known (up to logarithmic factors). To our knowledge, uniINF is the first parameter-free algorithm to achieve the BoBW property for the heavy-tailed MAB problem. Technically, we develop innovative techniques to achieve BoBW guarantees for Parameter-Free HTMABs, including a refined analysis for the dynamics of log-barrier, an auto-balancing learning rate scheduling scheme, an adaptive skipping-clipping loss tuning technique, and a stopping-time analysis for logarithmic regret.

Queue Scheduling with Adversarial Bandit Learning

In this paper, we study scheduling of a queueing system with zero knowledge of instantaneous network conditions. We consider a one-hop single-server queueing system consisting of $K$ queues, each with time-varying and non-stationary arrival and service rates. Our scheduling approach builds on an innovative combination of adversarial bandit learning and Lyapunov drift minimization, without knowledge of the instantaneous network state (the arrival and service rates) of each queue. We then present two novel algorithms \texttt{SoftMW} (SoftMaxWeight) and \texttt{SSMW} (Sliding-window SoftMaxWeight), both capable of stabilizing systems that can be stablized by some (possibly unknown) sequence of randomized policies whose time-variation satisfies a mild condition. We further generalize our results to the setting where arrivals and departures only have bounded moments instead of being deterministically bounded and propose \texttt{SoftMW+} and \texttt{SSMW+} that are capable of stabilizing the system. As a building block of our new algorithms, we also extend the classical \texttt{EXP3.S} (Auer et al., 2002) algorithm for multi-armed bandits to handle unboundedly large feedback signals, which can be of independent interest.

Banker Online Mirror Descent: A Universal Approach for Delayed Online Bandit Learning

We propose `Banker-OMD`, a novel framework generalizing the classical Online Mirror Descent (OMD) technique in the online learning literature. The `Banker-OMD` framework almost completely decouples feedback delay handling and the task-specific OMD algorithm design, thus allowing the easy design of new algorithms capable of easily and robustly handling feedback delays. Specifically, it offers a general methodology for achieving $\tilde{\mathcal O}(\sqrt{T} + \sqrt{D})$-style regret bounds in online bandit learning tasks with delayed feedback, where $T$ is the number of rounds and $D$ is the total feedback delay. We demonstrate the power of \texttt{Banker-OMD} by applications to two important bandit learning scenarios with delayed feedback, including delayed scale-free adversarial Multi-Armed Bandits (MAB) and delayed adversarial linear bandits. `Banker-OMD` leads to the first delayed scale-free adversarial MAB algorithm achieving $\tilde{\mathcal O}(\sqrt{K(D+T)}L)$ regret and the first delayed adversarial linear bandit algorithm achieving $\tilde{\mathcal O}(\text{poly}(n)(\sqrt{T} + \sqrt{D}))$ regret. As a corollary, the first application also implies $\tilde{\mathcal O}(\sqrt{KT}L)$ regret for non-delayed scale-free adversarial MABs, which is the first to match the $\Omega(\sqrt{KT}L)$ lower bound up to logarithmic factors and can be of independent interest.

Adaptive Best-of-Both-Worlds Algorithm for Heavy-Tailed Multi-Armed Bandits

In this paper, we generalize the concept of heavy-tailed multi-armed bandits to adversarial environments, and develop robust best-of-both-worlds algorithms for heavy-tailed multi-armed bandits (MAB), where losses have $\alpha$-th ($1<\alpha\le 2$) moments bounded by $\sigma^\alpha$, while the variances may not exist. Specifically, we design an algorithm \texttt{HTINF}, when the heavy-tail parameters $\alpha$ and $\sigma$ are known to the agent, \texttt{HTINF} simultaneously achieves the optimal regret for both stochastic and adversarial environments, without knowing the actual environment type a-priori. When $\alpha,\sigma$ are unknown, \texttt{HTINF} achieves a $\log T$-style instance-dependent regret in stochastic cases and $o(T)$ no-regret guarantee in adversarial cases. We further develop an algorithm \texttt{AdaTINF}, achieving $\mathcal O(\sigma K^{1-\nicefrac 1\alpha}T^{\nicefrac{1}{\alpha}})$ minimax optimal regret even in adversarial settings, without prior knowledge on $\alpha$ and $\sigma$. This result matches the known regret lower-bound (Bubeck et al., 2013), which assumed a stochastic environment and $\alpha$ and $\sigma$ are both known. To our knowledge, the proposed \texttt{HTINF} algorithm is the first to enjoy a best-of-both-worlds regret guarantee, and \texttt{AdaTINF} is the first algorithm that can adapt to both $\alpha$ and $\sigma$ to achieve optimal gap-indepedent regret bound in classical heavy-tailed stochastic MAB setting and our novel adversarial formulation.

Scale-Free Adversarial Multi-Armed Bandit with Arbitrary Feedback Delays

We consider the Scale-Free Adversarial Multi Armed Bandit (MAB) problem with unrestricted feedback delays. In contrast to the standard assumption that all losses are $[0,1]$-bounded, in our setting, losses can fall in a general bounded interval $[-L, L]$, unknown to the agent before-hand. Furthermore, the feedback of each arm pull can experience arbitrary delays. We propose an algorithm named \texttt{SFBanker} for this novel setting, which combines a recent banker online mirror descent technique and elaborately designed doubling tricks. We show that \texttt{SFBanker} achieves $\mathcal O(\sqrt{K(D+T)}L)\cdot {\rm polylog}(T, L)$ total regret, where $T$ is the total number of steps and $D$ is the total feedback delay. \texttt{SFBanker} also outperforms existing algorithm for non-delayed (i.e., $D=0$) scale-free adversarial MAB problem instances. We also present a variant of \texttt{SFBanker} for problem instances with non-negative losses (i.e., they range in $[0, L]$ for some unknown $L$), achieving an $\tilde{\mathcal O}(\sqrt{K(D+T)}L)$ total regret, which is near-optimal compared to the $\Omega(\sqrt{KT}+\sqrt{D\log K}L)$ lower-bound ([Cesa-Bianchi et al., 2016]).

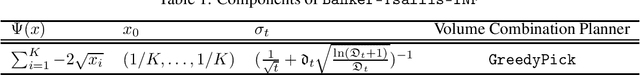
Banker Online Mirror Descent

We propose Banker-OMD, a novel framework generalizing the classical Online Mirror Descent (OMD) technique in online learning algorithm design. Banker-OMD allows algorithms to robustly handle delayed feedback, and offers a general methodology for achieving $\tilde{O}(\sqrt{T} + \sqrt{D})$-style regret bounds in various delayed-feedback online learning tasks, where $T$ is the time horizon length and $D$ is the total feedback delay. We demonstrate the power of Banker-OMD with applications to three important bandit scenarios with delayed feedback, including delayed adversarial Multi-armed bandits (MAB), delayed adversarial linear bandits, and a novel delayed best-of-both-worlds MAB setting. Banker-OMD achieves nearly-optimal performance in all the three settings. In particular, it leads to the first delayed adversarial linear bandit algorithm achieving $\tilde{O}(\text{poly}(n)(\sqrt{T} + \sqrt{D}))$ regret.