Diffusion-Based Cross-Modal Feature Extraction for Multi-Label Classification

Multi-label classification has broad applications and depends on powerful representations capable of capturing multi-label interactions. We introduce \textit{Diff-Feat}, a simple but powerful framework that extracts intermediate features from pre-trained diffusion-Transformer models for images and text, and fuses them for downstream tasks. We observe that for vision tasks, the most discriminative intermediate feature along the diffusion process occurs at the middle step and is located in the middle block in Transformer. In contrast, for language tasks, the best feature occurs at the noise-free step and is located in the deepest block. In particular, we observe a striking phenomenon across varying datasets: a mysterious "Layer $12$" consistently yields the best performance on various downstream classification tasks for images (under DiT-XL/2-256$\times$256). We devise a heuristic local-search algorithm that pinpoints the locally optimal "image-text"$\times$"block-timestep" pair among a few candidates, avoiding an exhaustive grid search. A simple fusion-linear projection followed by addition-of the selected representations yields state-of-the-art performance: 98.6\% mAP on MS-COCO-enhanced and 45.7\% mAP on Visual Genome 500, surpassing strong CNN, graph, and Transformer baselines by a wide margin. t-SNE and clustering metrics further reveal that \textit{Diff-Feat} forms tighter semantic clusters than unimodal counterparts. The code is available at https://github.com/lt-0123/Diff-Feat.

Modeling High-Dimensional Data with Unknown Cut Points: A Fusion Penalized Logistic Threshold Regression

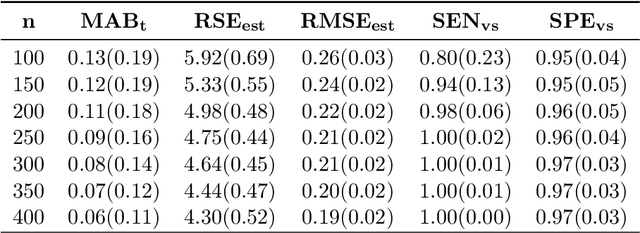
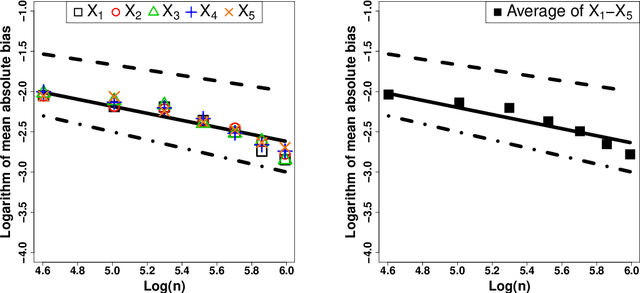
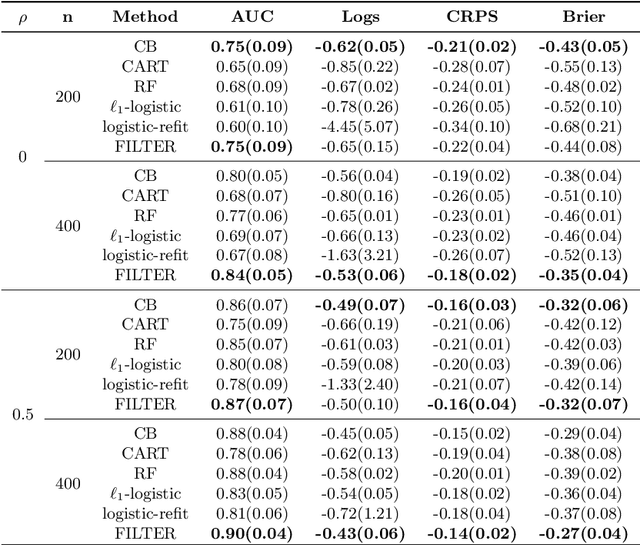
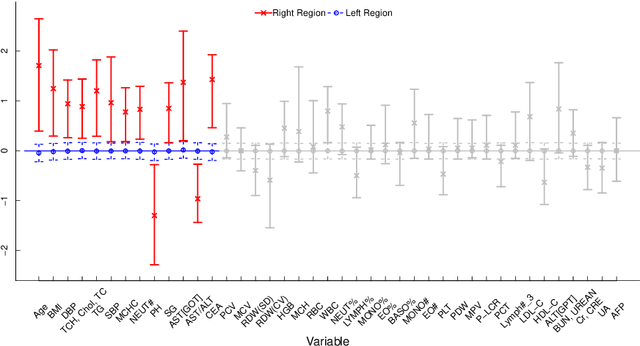
In traditional logistic regression models, the link function is often assumed to be linear and continuous in predictors. Here, we consider a threshold model that all continuous features are discretized into ordinal levels, which further determine the binary responses. Both the threshold points and regression coefficients are unknown and to be estimated. For high dimensional data, we propose a fusion penalized logistic threshold regression (FILTER) model, where a fused lasso penalty is employed to control the total variation and shrink the coefficients to zero as a method of variable selection. Under mild conditions on the estimate of unknown threshold points, we establish the non-asymptotic error bound for coefficient estimation and the model selection consistency. With a careful characterization of the error propagation, we have also shown that the tree-based method, such as CART, fulfill the threshold estimation conditions. We find the FILTER model is well suited in the problem of early detection and prediction for chronic disease like diabetes, using physical examination data. The finite sample behavior of our proposed method are also explored and compared with extensive Monte Carlo studies, which supports our theoretical discoveries.