Variational Bayesian modelling of mixed-effects

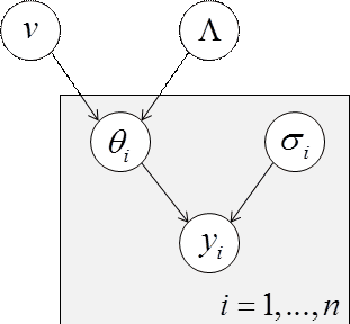
This note is concerned with an accurate and computationally efficient variational bayesian treatment of mixed-effects modelling. We focus on group studies, i.e. empirical studies that report multiple measurements acquired in multiple subjects. When approached from a bayesian perspective, such mixed-effects models typically rely upon a hierarchical generative model of the data, whereby both within- and between-subject effects contribute to the overall observed variance. The ensuing VB scheme can be used to assess statistical significance at the group level and/or to capture inter-individual differences. Alternatively, it can be seen as an adaptive regularization procedure, which iteratively learns the corresponding within-subject priors from estimates of the group distribution of effects of interest (cf. so-called "empirical bayes" approaches). We outline the mathematical derivation of the ensuing VB scheme, whose open-source implementation is available as part the VBA toolbox.

The variational Laplace approach to approximate Bayesian inference

Variational approaches to approximate Bayesian inference provide very efficient means of performing parameter estimation and model selection. Among these, so-called variational-Laplace or VL schemes rely on Gaussian approximations to posterior densities on model parameters. In this note, we review the main variants of VL approaches, that follow from considering nonlinear models of continuous and/or categorical data. En passant, we also derive a few novel theoretical results that complete the portfolio of existing analyses of variational Bayesian approaches, including investigations of their asymptotic convergence. We also suggest practical ways of extending existing VL approaches to hierarchical generative models that include (e.g., precision) hyperparameters.

On parameters transformations for emulating sparse priors using variational-Laplace inference

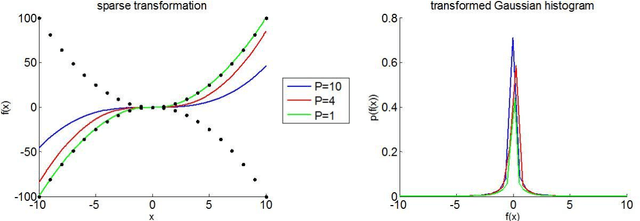
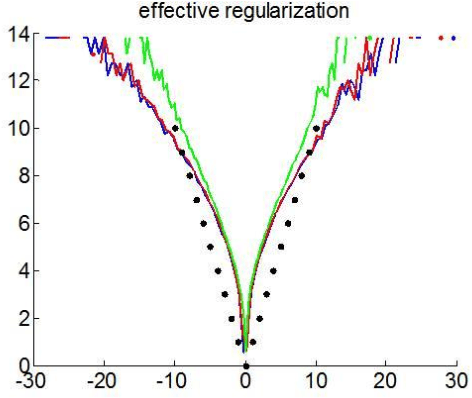
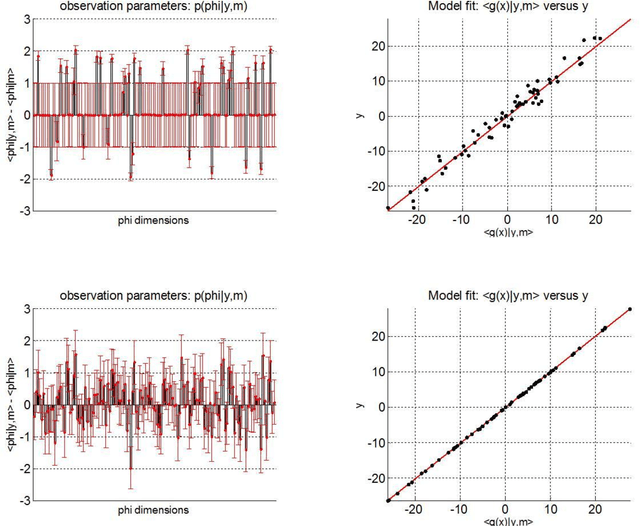
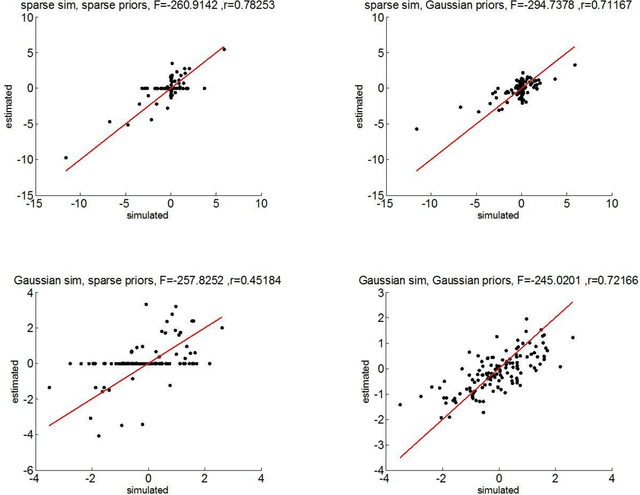
So-called sparse estimators arise in the context of model fitting, when one a priori assumes that only a few (unknown) model parameters deviate from zero. Sparsity constraints can be useful when the estimation problem is under-determined, i.e. when number of model parameters is much higher than the number of data points. Typically, such constraints are enforced by minimizing the L1 norm, which yields the so-called LASSO estimator. In this work, we propose a simple parameter transform that emulates sparse priors without sacrificing the simplicity and robustness of L2-norm regularization schemes. We show how L1 regularization can be obtained with a "sparsify" remapping of parameters under normal Bayesian priors, and we demonstrate the ensuing variational Laplace approach using Monte-Carlo simulations.

Semi-analytical approximations to statistical moments of sigmoid and softmax mappings of normal variables

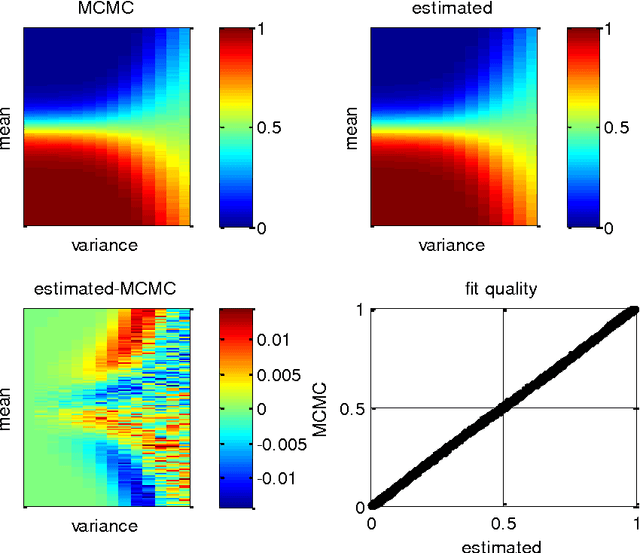
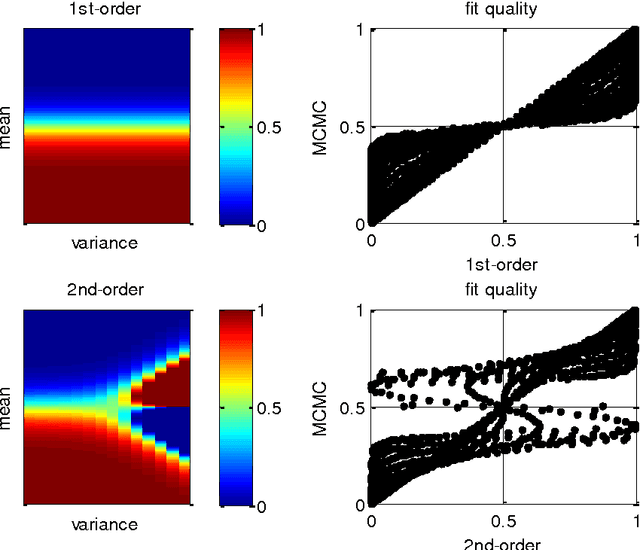
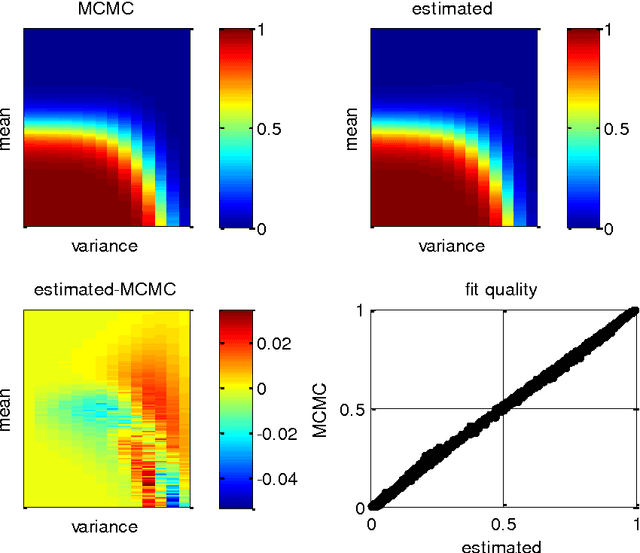
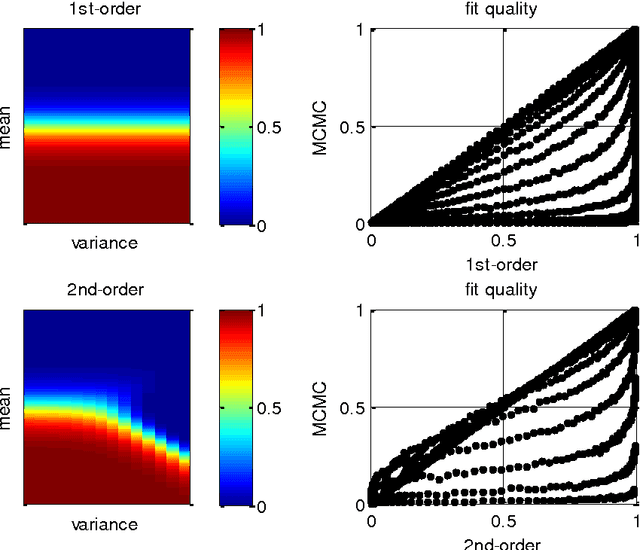
This note is concerned with accurate and computationally efficient approximations of moments of Gaussian random variables passed through sigmoid or softmax mappings. These approximations are semi-analytical (i.e. they involve the numerical adjustment of parametric forms) and highly accurate (they yield 5% error at most). We also highlight a few niche applications of these approximations, which arise in the context of, e.g., drift-diffusion models of decision making or non-parametric data clustering approaches. We provide these as examples of efficient alternatives to more tedious derivations that would be needed if one was to approach the underlying mathematical issues in a more formal way. We hope that this technical note will be helpful to modellers facing similar mathematical issues, although maybe stemming from different academic prospects.