Robust Quickest Correlation Change Detection in High-Dimensional Random Vectors

Detecting changes in high-dimensional vectors presents significant challenges, especially when the post-change distribution is unknown and time-varying. This paper introduces a novel robust algorithm for correlation change detection in high-dimensional data. The approach utilizes the summary statistic of the maximum magnitude correlation coefficient to detect the change. This summary statistic captures the level of correlation present in the data but also has an asymptotic density. The robust test is designed using the asymptotic density. The proposed approach is robust because it can help detect a change in correlation level from some known level to unknown, time-varying levels. The proposed test is also computationally efficient and valid for a broad class of data distributions. The effectiveness of the proposed algorithm is demonstrated on simulated data.

Learning Combined Set Covering and Traveling Salesman Problem

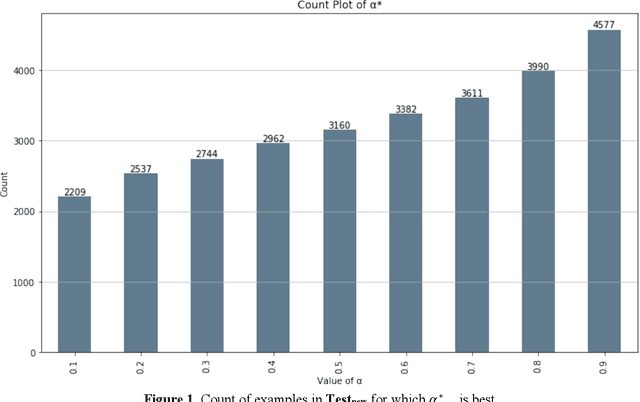
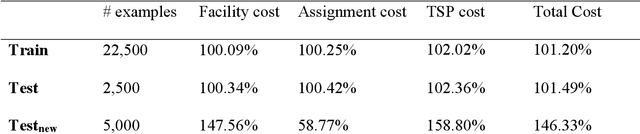
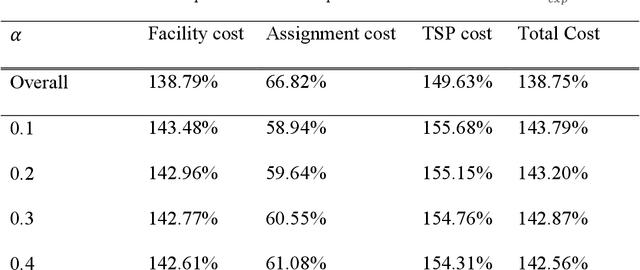
The Traveling Salesman Problem is one of the most intensively studied combinatorial optimization problems due both to its range of real-world applications and its computational complexity. When combined with the Set Covering Problem, it raises even more issues related to tractability and scalability. We study a combined Set Covering and Traveling Salesman problem and provide a mixed integer programming formulation to solve the problem. Motivated by applications where the optimal policy needs to be updated on a regular basis and repetitively solving this via MIP can be computationally expensive, we propose a machine learning approach to effectively deal with this problem by providing an opportunity to learn from historical optimal solutions that are derived from the MIP formulation. We also present a case study using the vaccine distribution chain of the World Health Organization, and provide numerical results with data derived from four countries in sub-Saharan Africa.

Optimizing vaccine distribution networks in low and middle-income countries

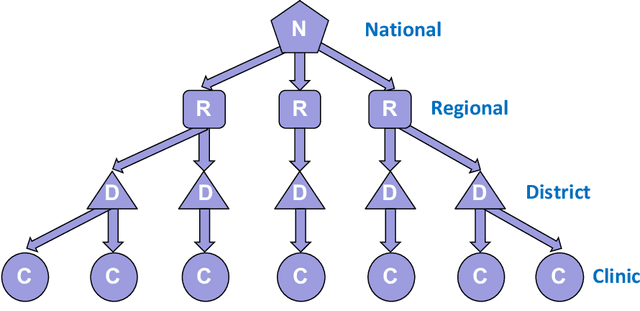
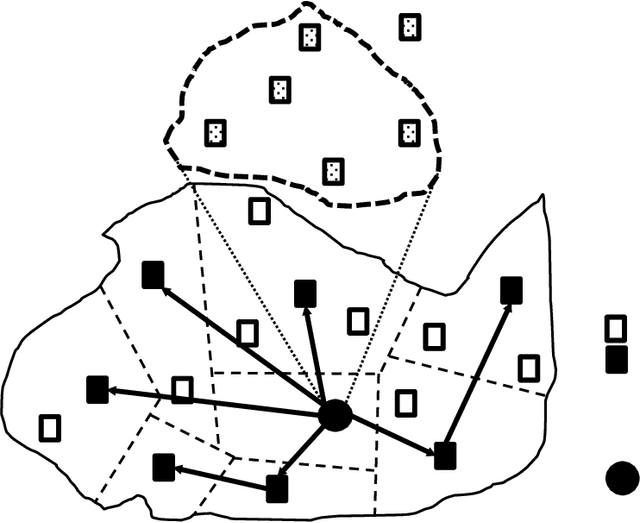
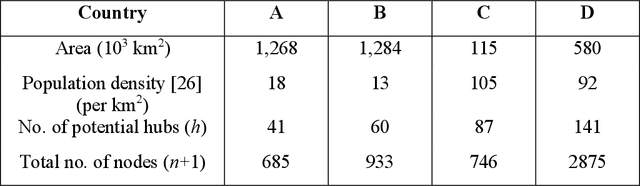
Vaccination has been proven to be the most effective method to prevent infectious diseases. However, there are still millions of children in low and middle-income countries who are not covered by routine vaccines and remain at risk. The World Health Organization's Expanded Programme on Immunization (WHO-EPI) was designed to provide universal childhood vaccine access for children across the world and in this work, we address the design of the distribution network for WHO-EPI vaccines. In particular, we formulate the network design problem as a mixed integer program (MIP) and present a new algorithm for typical problems that are too large to be solved using commercial MIP software. We test the algorithm using data derived from four different countries in sub-Saharan Africa and show that the algorithm is able to obtain high-quality solutions for even the largest problems within a few minutes.