Distributed Control Barrier Functions for Safe Multi-Vehicle Navigation in Heterogeneous USV Fleets

Collision avoidance in heterogeneous fleets of uncrewed vessels is challenging because the decision-making processes and controllers often differ between platforms, and it is further complicated by the limitations on sharing trajectories and control values in real-time. This paper presents a pragmatic approach that addresses these issues by adding a control filter on each autonomous vehicle that assumes worst-case behavior from other contacts, including crewed vessels. This distributed safety control filter is developed using control barrier function (CBF) theory and the application is clearly described to ensure explainability of these safety-critical methods. This work compares the worst-case CBF approach with a Collision Regulations (COLREGS) behavior-based approach in simulated encounters. Real-world experiments with three different uncrewed vessels and a human operated vessel were performed to confirm the approach is effective across a range of platforms and is robust to uncooperative behavior from human operators. Results show that combining both CBF methods and COLREGS behaviors achieves the best safety and efficiency.

Automatic Grid Updates for Kolmogorov-Arnold Networks using Layer Histograms

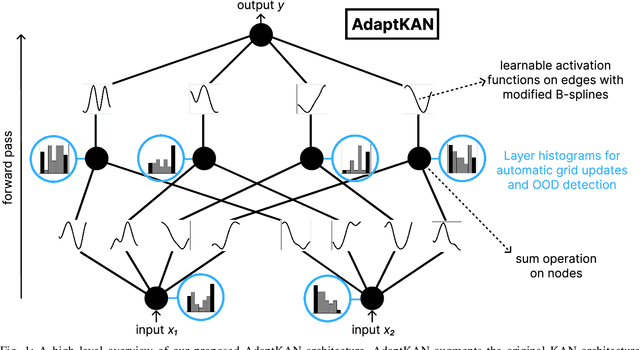
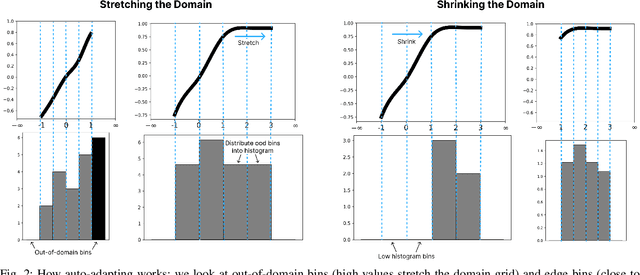
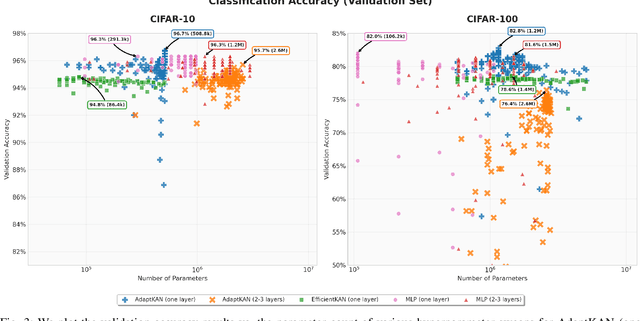
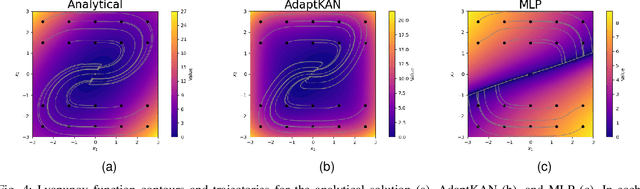
Kolmogorov-Arnold Networks (KANs) are a class of neural networks that have received increased attention in recent literature. In contrast to MLPs, KANs leverage parameterized, trainable activation functions and offer several benefits including improved interpretability and higher accuracy on learning symbolic equations. However, the original KAN architecture requires adjustments to the domain discretization of the network (called the "domain grid") during training, creating extra overhead for the user in the training process. Typical KAN layers are not designed with the ability to autonomously update their domains in a data-driven manner informed by the changing output ranges of previous layers. As an added benefit, this histogram algorithm may also be applied towards detecting out-of-distribution (OOD) inputs in a variety of settings. We demonstrate that AdaptKAN exceeds or matches the performance of prior KAN architectures and MLPs on four different tasks: learning scientific equations from the Feynman dataset, image classification from frozen features, learning a control Lyapunov function, and detecting OOD inputs on the OpenOOD v1.5 benchmark.

Triangle-Decomposable Graphs for Isoperimetric Robots

Isoperimetric robots are large scale, untethered inflatable robots that can undergo large shape changes, but have only been demonstrated in one 3D shape -- an octahedron. These robots consist of independent triangles that can change shape while maintaining their perimeter by moving the relative position of their joints. We introduce an optimization routine that determines if an arbitrary graph can be partitioned into unique triangles, and thus be constructed as an isoperimetric robotic system. We enumerate all minimally rigid graphs that can be constructed with unique triangles up to 9 nodes (7 triangles), and characterize the workspace of one node of each these robots. We also present a method for constructing larger graphs that can be partitioned by assembling subgraphs that are already partitioned into triangles. This enables a wide variety of isoperimetric robot configurations.