Online Newton Method for Bandit Convex Optimisation

We introduce a computationally efficient algorithm for zeroth-order bandit convex optimisation and prove that in the adversarial setting its regret is at most $d^{3.5} \sqrt{n} \mathrm{polylog}(n, d)$ with high probability where $d$ is the dimension and $n$ is the time horizon. In the stochastic setting the bound improves to $M d^{2} \sqrt{n} \mathrm{polylog}(n, d)$ where $M \in [d^{-1/2}, d^{-1 / 4}]$ is a constant that depends on the geometry of the constraint set and the desired computational properties.

Scale-free Unconstrained Online Learning for Curved Losses

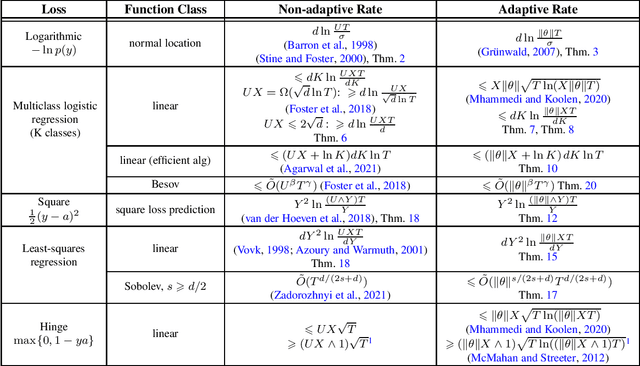
A sequence of works in unconstrained online convex optimisation have investigated the possibility of adapting simultaneously to the norm $U$ of the comparator and the maximum norm $G$ of the gradients. In full generality, matching upper and lower bounds are known which show that this comes at the unavoidable cost of an additive $G U^3$, which is not needed when either $G$ or $U$ is known in advance. Surprisingly, recent results by Kempka et al. (2019) show that no such price for adaptivity is needed in the specific case of $1$-Lipschitz losses like the hinge loss. We follow up on this observation by showing that there is in fact never a price to pay for adaptivity if we specialise to any of the other common supervised online learning losses: our results cover log loss, (linear and non-parametric) logistic regression, square loss prediction, and (linear and non-parametric) least-squares regression. We also fill in several gaps in the literature by providing matching lower bounds with an explicit dependence on $U$. In all cases we obtain scale-free algorithms, which are suitably invariant under rescaling of the data. Our general goal is to establish achievable rates without concern for computational efficiency, but for linear logistic regression we also provide an adaptive method that is as efficient as the recent non-adaptive algorithm by Agarwal et al. (2021).