Statistical Agnostic Regression: a machine learning method to validate regression models

Regression analysis is a central topic in statistical modeling, aiming to estimate the relationships between a dependent variable, commonly referred to as the response variable, and one or more independent variables, i.e., explanatory variables. Linear regression is by far the most popular method for performing this task in several fields of research, such as prediction, forecasting, or causal inference. Beyond various classical methods to solve linear regression problems, such as Ordinary Least Squares, Ridge, or Lasso regressions - which are often the foundation for more advanced machine learning (ML) techniques - the latter have been successfully applied in this scenario without a formal definition of statistical significance. At most, permutation or classical analyses based on empirical measures (e.g., residuals or accuracy) have been conducted to reflect the greater ability of ML estimations for detection. In this paper, we introduce a method, named Statistical Agnostic Regression (SAR), for evaluating the statistical significance of an ML-based linear regression based on concentration inequalities of the actual risk using the analysis of the worst case. To achieve this goal, similar to the classification problem, we define a threshold to establish that there is sufficient evidence with a probability of at least 1-eta to conclude that there is a linear relationship in the population between the explanatory (feature) and the response (label) variables. Simulations in only two dimensions demonstrate the ability of the proposed agnostic test to provide a similar analysis of variance given by the classical $F$ test for the slope parameter.

Is K-fold cross validation the best model selection method for Machine Learning?

As a technique that can compactly represent complex patterns, machine learning has significant potential for predictive inference. K-fold cross-validation (CV) is the most common approach to ascertaining the likelihood that a machine learning outcome is generated by chance and frequently outperforms conventional hypothesis testing. This improvement uses measures directly obtained from machine learning classifications, such as accuracy, that do not have a parametric description. To approach a frequentist analysis within machine learning pipelines, a permutation test or simple statistics from data partitions (i.e. folds) can be added to estimate confidence intervals. Unfortunately, neither parametric nor non-parametric tests solve the inherent problems around partitioning small sample-size datasets and learning from heterogeneous data sources. The fact that machine learning strongly depends on the learning parameters and the distribution of data across folds recapitulates familiar difficulties around excess false positives and replication. The origins of this problem are demonstrated by simulating common experimental circumstances, including small sample sizes, low numbers of predictors, and heterogeneous data sources. A novel statistical test based on K-fold CV and the Upper Bound of the actual error (K-fold CUBV) is composed, where uncertain predictions of machine learning with CV are bounded by the \emph{worst case} through the evaluation of concentration inequalities. Probably Approximately Correct-Bayesian upper bounds for linear classifiers in combination with K-fold CV is used to estimate the empirical error. The performance with neuroimaging datasets suggests this is a robust criterion for detecting effects, validating accuracy values obtained from machine learning whilst avoiding excess false positives.

A hypothesis-driven method based on machine learning for neuroimaging data analysis

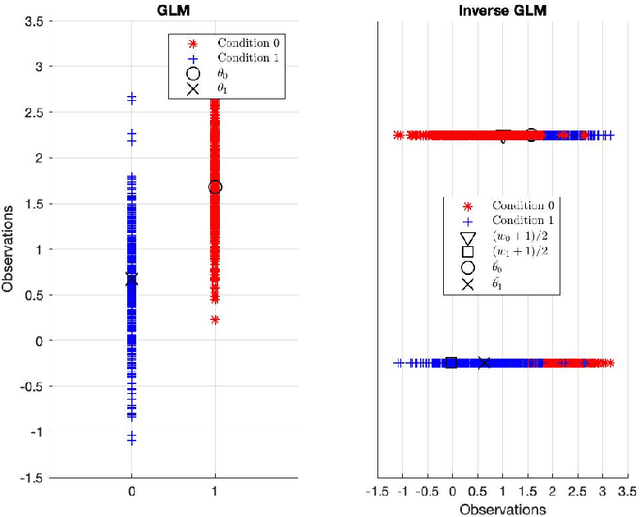
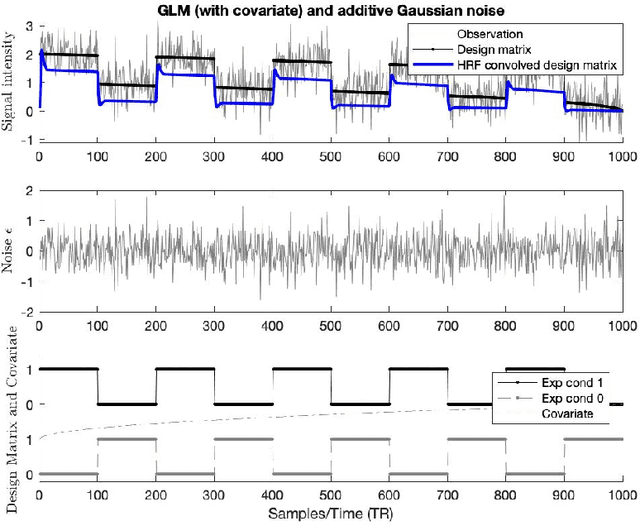
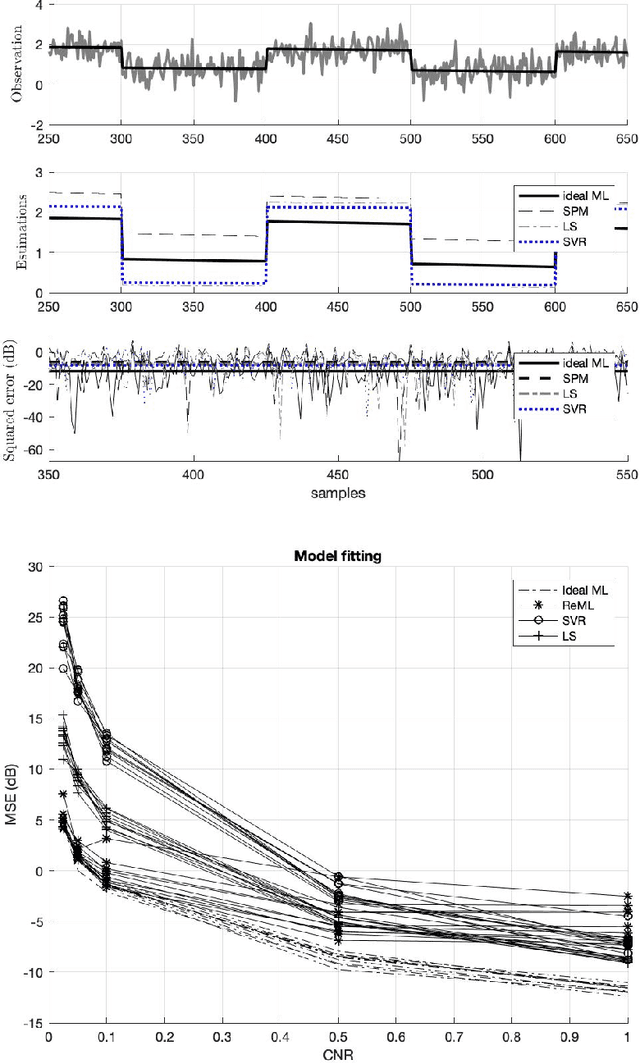
There remains an open question about the usefulness and the interpretation of Machine learning (MLE) approaches for discrimination of spatial patterns of brain images between samples or activation states. In the last few decades, these approaches have limited their operation to feature extraction and linear classification tasks for between-group inference. In this context, statistical inference is assessed by randomly permuting image labels or by the use of random effect models that consider between-subject variability. These multivariate MLE-based statistical pipelines, whilst potentially more effective for detecting activations than hypotheses-driven methods, have lost their mathematical elegance, ease of interpretation, and spatial localization of the ubiquitous General linear Model (GLM). Recently, the estimation of the conventional GLM has been demonstrated to be connected to an univariate classification task when the design matrix is expressed as a binary indicator matrix. In this paper we explore the complete connection between the univariate GLM and MLE \emph{regressions}. To this purpose we derive a refined statistical test with the GLM based on the parameters obtained by a linear Support Vector Regression (SVR) in the \emph{inverse} problem (SVR-iGLM). Subsequently, random field theory (RFT) is employed for assessing statistical significance following a conventional GLM benchmark. Experimental results demonstrate how parameter estimations derived from each model (mainly GLM and SVR) result in different experimental design estimates that are significantly related to the predefined functional task. Moreover, using real data from a multisite initiative the proposed MLE-based inference demonstrates statistical power and the control of false positives, outperforming the regular GLM.