A Modern Self-Referential Weight Matrix That Learns to Modify Itself

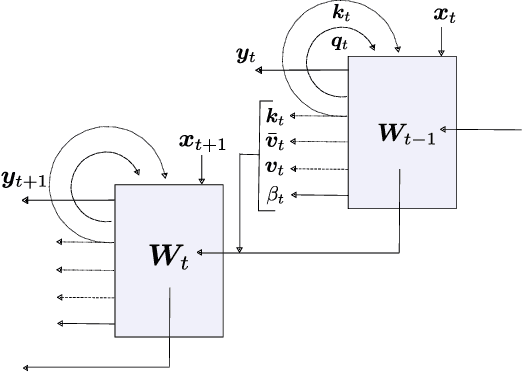
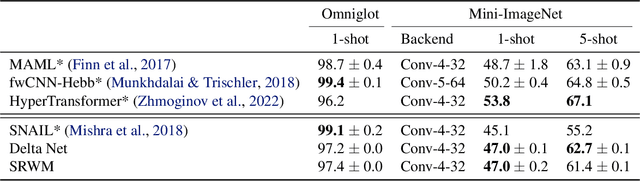
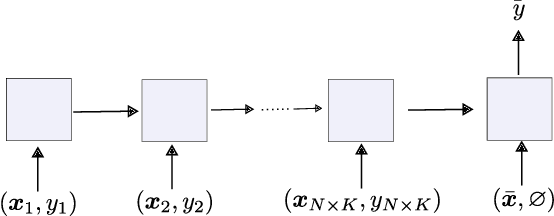
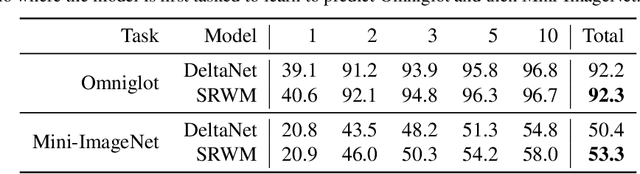
The weight matrix (WM) of a neural network (NN) is its program. The programs of many traditional NNs are learned through gradient descent in some error function, then remain fixed. The WM of a self-referential NN, however, can keep rapidly modifying all of itself during runtime. In principle, such NNs can meta-learn to learn, and meta-meta-learn to meta-learn to learn, and so on, in the sense of recursive self-improvement. While NN architectures potentially capable of implementing such behavior have been proposed since the '90s, there have been few if any practical studies. Here we revisit such NNs, building upon recent successes of fast weight programmers and closely related linear Transformers. We propose a scalable self-referential WM (SRWM) that uses outer products and the delta update rule to modify itself. We evaluate our SRWM in supervised few-shot learning and in multi-task reinforcement learning with procedurally generated game environments. Our experiments demonstrate both practical applicability and competitive performance of the proposed SRWM. Our code is public.

Improving Baselines in the Wild

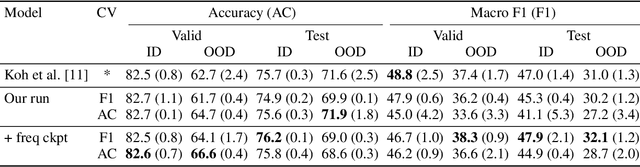
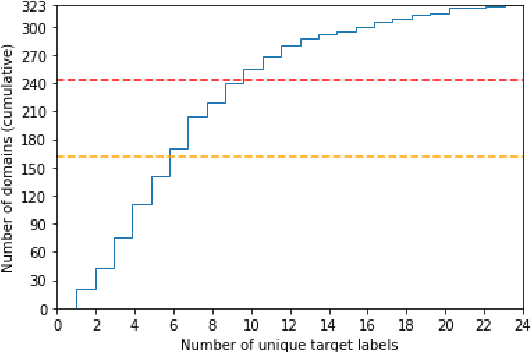
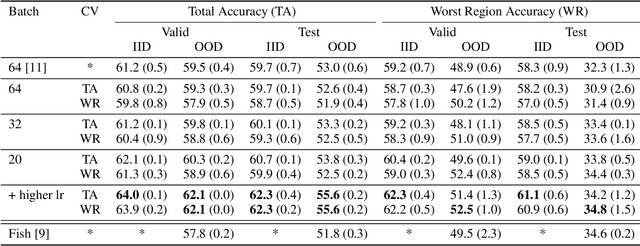
We share our experience with the recently released WILDS benchmark, a collection of ten datasets dedicated to developing models and training strategies which are robust to domain shifts. Several experiments yield a couple of critical observations which we believe are of general interest for any future work on WILDS. Our study focuses on two datasets: iWildCam and FMoW. We show that (1) Conducting separate cross-validation for each evaluation metric is crucial for both datasets, (2) A weak correlation between validation and test performance might make model development difficult for iWildCam, (3) Minor changes in the training of hyper-parameters improve the baseline by a relatively large margin (mainly on FMoW), (4) There is a strong correlation between certain domains and certain target labels (mainly on iWildCam). To the best of our knowledge, no prior work on these datasets has reported these observations despite their obvious importance. Our code is public.

Going Beyond Linear Transformers with Recurrent Fast Weight Programmers

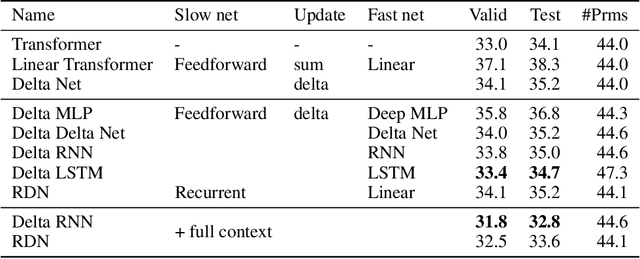
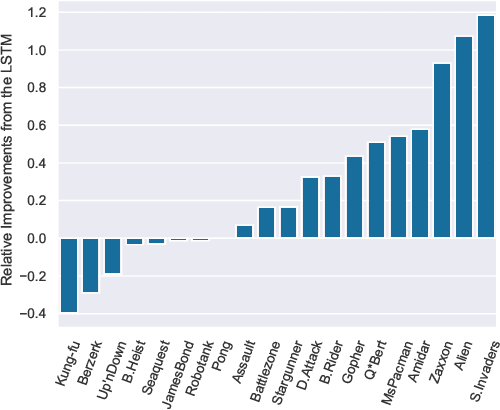
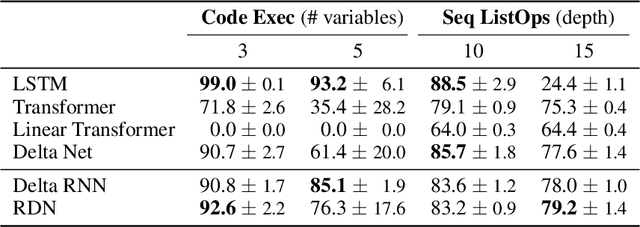
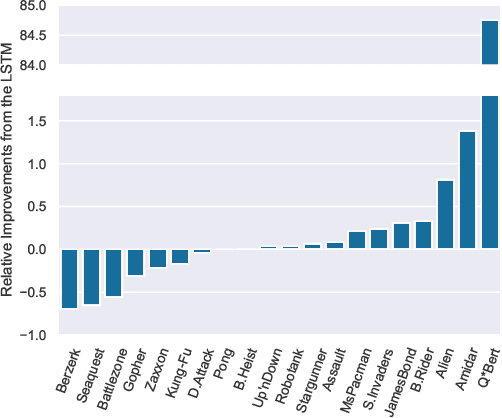
Transformers with linearised attention ("linear Transformers") have demonstrated the practical scalability and effectiveness of outer product-based Fast Weight Programmers (FWPs) from the '90s. However, the original FWP formulation is more general than the one of linear Transformers: a slow neural network (NN) continually reprograms the weights of a fast NN with arbitrary NN architectures. In existing linear Transformers, both NNs are feedforward and consist of a single layer. Here we explore new variations by adding recurrence to the slow and fast nets. We evaluate our novel recurrent FWPs (RFWPs) on two synthetic algorithmic tasks (code execution and sequential ListOps), Wikitext-103 language models, and on the Atari 2600 2D game environment. Our models exhibit properties of Transformers and RNNs. In the reinforcement learning setting, we report large improvements over LSTM in several Atari games. Our code is public.

Linear Transformers Are Secretly Fast Weight Memory Systems

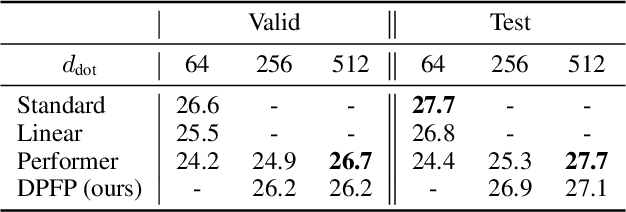
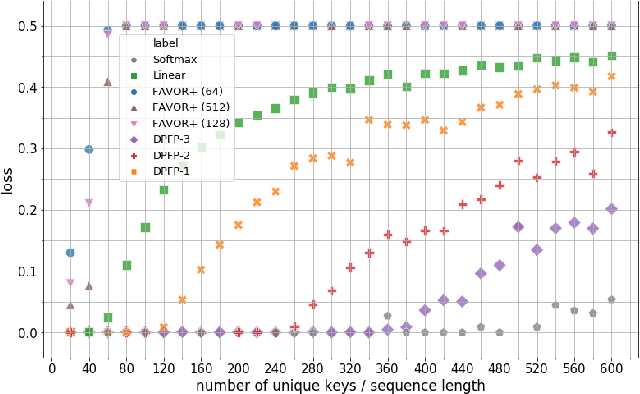
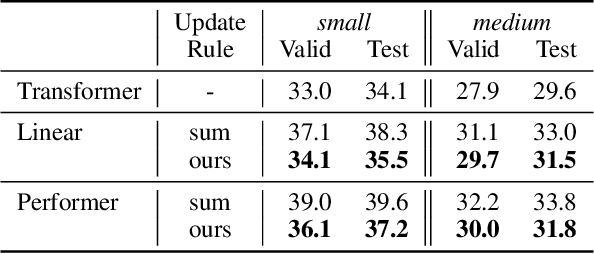
We show the formal equivalence of linearised self-attention mechanisms and fast weight memories from the early '90s. From this observation we infer a memory capacity limitation of recent linearised softmax attention variants. With finite memory, a desirable behaviour of fast weight memory models is to manipulate the contents of memory and dynamically interact with it. Inspired by previous work on fast weights, we propose to replace the update rule with an alternative rule yielding such behaviour. We also propose a new kernel function to linearise attention, balancing simplicity and effectiveness. We conduct experiments on synthetic retrieval problems as well as standard machine translation and language modelling tasks which demonstrate the benefits of our methods.

Learning Associative Inference Using Fast Weight Memory

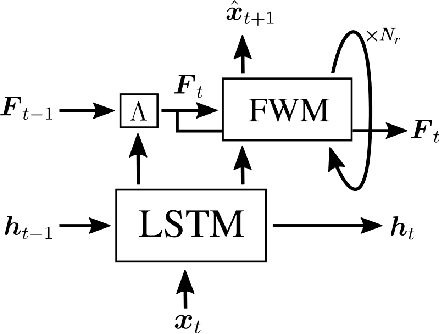
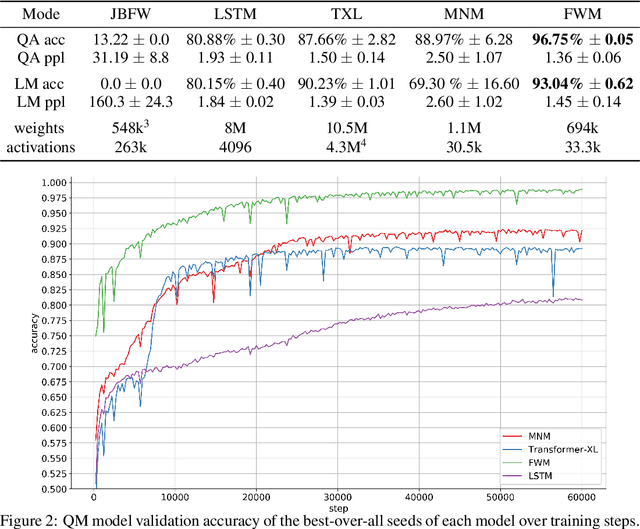
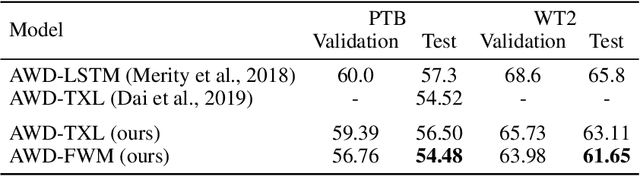
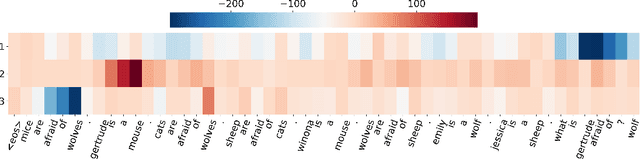
Humans can quickly associate stimuli to solve problems in novel contexts. Our novel neural network model learns state representations of facts that can be composed to perform such associative inference. To this end, we augment the LSTM model with an associative memory, dubbed Fast Weight Memory (FWM). Through differentiable operations at every step of a given input sequence, the LSTM updates and maintains compositional associations stored in the rapidly changing FWM weights. Our model is trained end-to-end by gradient descent and yields excellent performance on compositional language reasoning problems, meta-reinforcement-learning for POMDPs, and small-scale word-level language modelling.

Enhancing the Transformer with Explicit Relational Encoding for Math Problem Solving

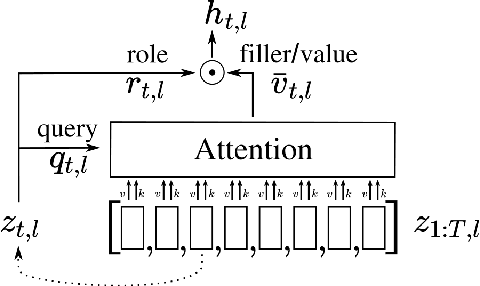
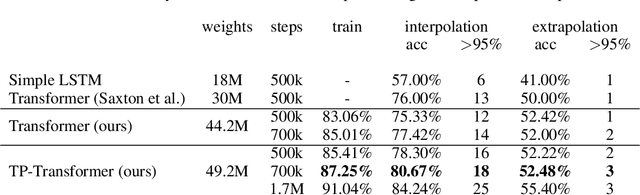
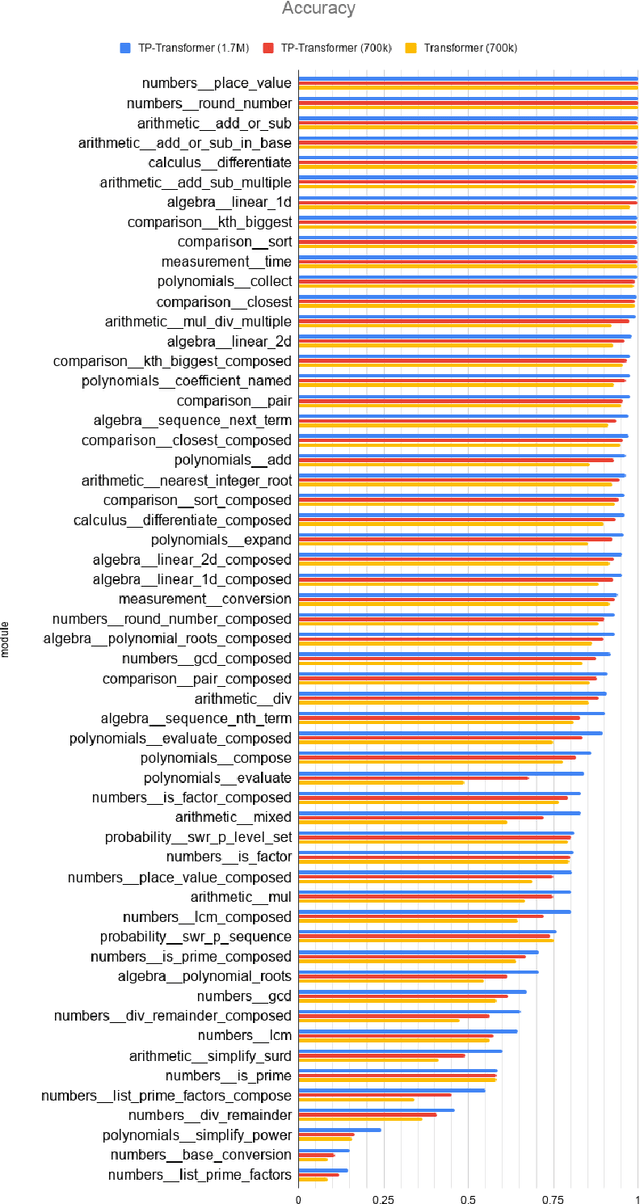
We incorporate Tensor-Product Representations within the Transformer in order to better support the explicit representation of relation structure. Our Tensor-Product Transformer (TP-Transformer) sets a new state of the art on the recently-introduced Mathematics Dataset containing 56 categories of free-form math word-problems. The essential component of the model is a novel attention mechanism, called TP-Attention, which explicitly encodes the relations between each Transformer cell and the other cells from which values have been retrieved by attention. TP-Attention goes beyond linear combination of retrieved values, strengthening representation-building and resolving ambiguities introduced by multiple layers of standard attention. The TP-Transformer's attention maps give better insights into how it is capable of solving the Mathematics Dataset's challenging problems. Pretrained models and code will be made available after publication.

Learning to Reason with Third-Order Tensor Products

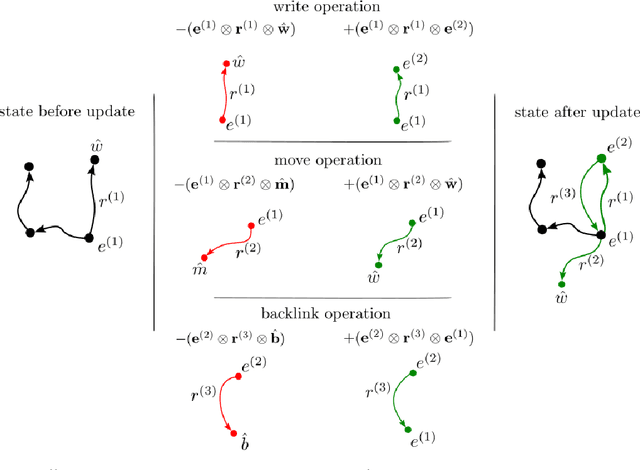
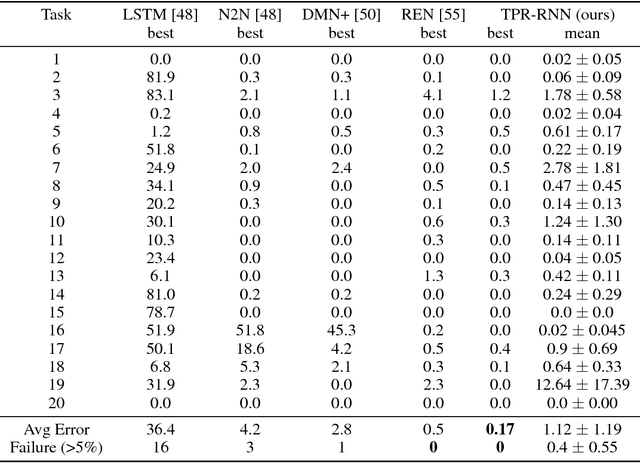
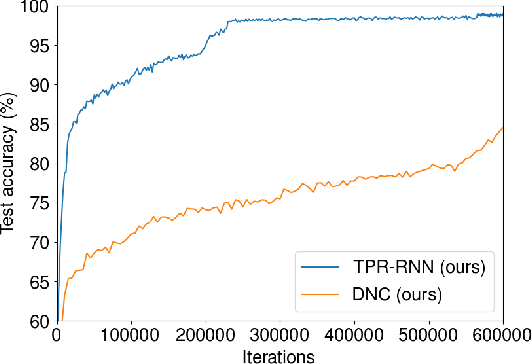
We combine Recurrent Neural Networks with Tensor Product Representations to learn combinatorial representations of sequential data. This improves symbolic interpretation and systematic generalisation. Our architecture is trained end-to-end through gradient descent on a variety of simple natural language reasoning tasks, significantly outperforming the latest state-of-the-art models in single-task and all-tasks settings. We also augment a subset of the data such that training and test data exhibit large systematic differences and show that our approach generalises better than the previous state-of-the-art.