Translating Answer-Set Programs into Bit-Vector Logic

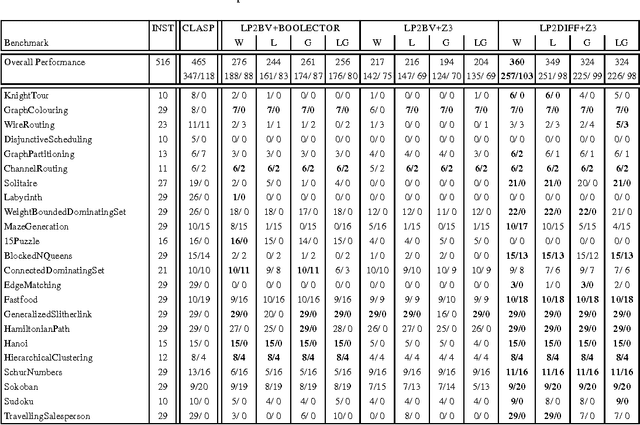
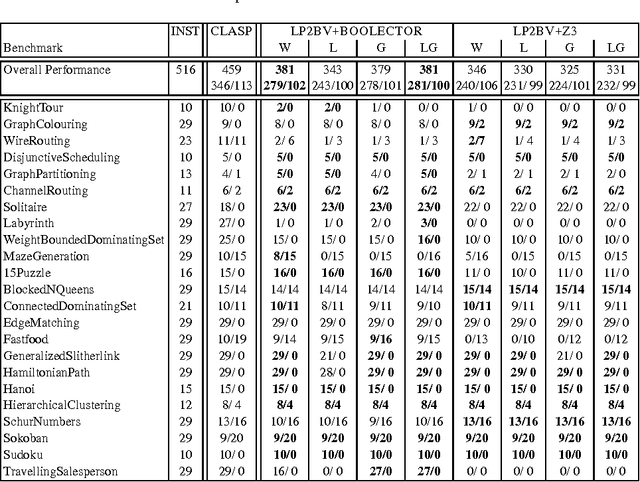
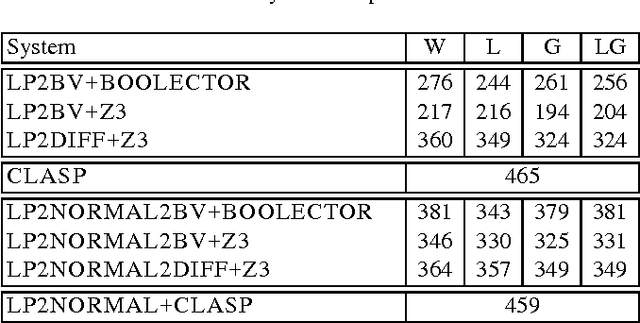
Answer set programming (ASP) is a paradigm for declarative problem solving where problems are first formalized as rule sets, i.e., answer-set programs, in a uniform way and then solved by computing answer sets for programs. The satisfiability modulo theories (SMT) framework follows a similar modelling philosophy but the syntax is based on extensions of propositional logic rather than rules. Quite recently, a translation from answer-set programs into difference logic was provided---enabling the use of particular SMT solvers for the computation of answer sets. In this paper, the translation is revised for another SMT fragment, namely that based on fixed-width bit-vector theories. Thus, even further SMT solvers can be harnessed for the task of computing answer sets. The results of a preliminary experimental comparison are also reported. They suggest a level of performance which is similar to that achieved via difference logic.

Bounded LTL Model Checking with Stable Models

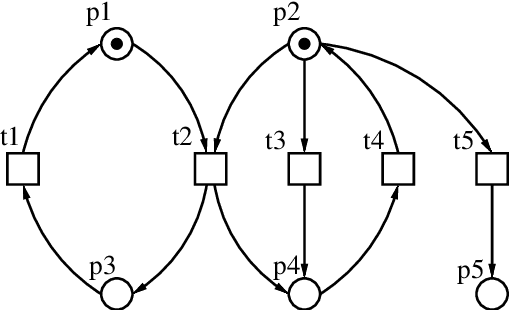
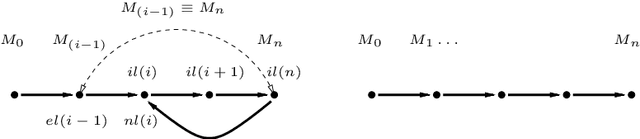
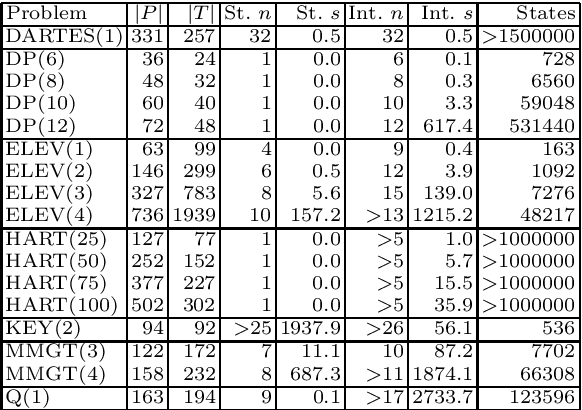
In this paper bounded model checking of asynchronous concurrent systems is introduced as a promising application area for answer set programming. As the model of asynchronous systems a generalisation of communicating automata, 1-safe Petri nets, are used. It is shown how a 1-safe Petri net and a requirement on the behaviour of the net can be translated into a logic program such that the bounded model checking problem for the net can be solved by computing stable models of the corresponding program. The use of the stable model semantics leads to compact encodings of bounded reachability and deadlock detection tasks as well as the more general problem of bounded model checking of linear temporal logic. Correctness proofs of the devised translations are given, and some experimental results using the translation and the Smodels system are presented.