ASyMOB: Algebraic Symbolic Mathematical Operations Benchmark

Large language models (LLMs) are rapidly approaching the level of proficiency in university-level symbolic mathematics required for applications in advanced science and technology. However, existing benchmarks fall short in assessing the core skills of LLMs in symbolic mathematics-such as integration, differential equations, and algebraic simplification. To address this gap, we introduce ASyMOB, a novel assessment framework focused exclusively on symbolic manipulation, featuring 17,092 unique math challenges, organized by similarity and complexity. ASyMOB enables analysis of LLM generalization capabilities by comparing performance in problems that differ by simple numerical or symbolic `perturbations'. Evaluated LLMs exhibit substantial degradation in performance for all perturbation types (up to -70.3%), suggesting reliance on memorized patterns rather than deeper understanding of symbolic math, even among models achieving high baseline accuracy. Comparing LLM performance to computer algebra systems, we identify examples where they fail while LLMs succeed, as well as problems solved only by combining both approaches. Models capable of integrated code execution yielded higher accuracy compared to their performance without code, particularly stabilizing weaker models (up to +33.1% for certain perturbation types). Notably, the most advanced models (o4-mini, Gemini 2.5 Flash) demonstrate not only high symbolic math proficiency (scoring 96.8% and 97.6% on the unperturbed set), but also remarkable robustness against perturbations, (-21.7% and -21.2% vs. average -50.4% for the other models). This may indicate a recent "phase transition" in the generalization capabilities of frontier LLMs. It remains to be seen whether the path forward lies in deeper integration with sophisticated external tools, or in developing models so capable that symbolic math systems like CAS become unnecessary.

From Euler to AI: Unifying Formulas for Mathematical Constants

The constant $\pi$ has fascinated scholars for centuries, inspiring the derivation of countless formulas rooted in profound mathematical insight. This abundance of formulas raises a question: Are they interconnected, and can a unifying structure explain their relationships? We propose a systematic methodology for discovering and proving formula equivalences, leveraging modern large language models, large-scale data processing, and novel mathematical algorithms. Analyzing 457,145 arXiv papers, over a third of the validated formulas for $\pi$ were proven to be derivable from a single mathematical object - including formulas by Euler, Gauss, Lord Brouncker, and newer ones from algorithmic discoveries by the Ramanujan Machine. Our approach extends to other constants, such as $e$, $\zeta(3)$, and Catalan's constant, proving its broad applicability. This work represents a step toward the automatic unification of mathematical knowledge, laying a foundation for AI-driven discoveries of connections across scientific domains.

Unsupervised Discovery of Formulas for Mathematical Constants

Ongoing efforts that span over decades show a rise of AI methods for accelerating scientific discovery, yet accelerating discovery in mathematics remains a persistent challenge for AI. Specifically, AI methods were not effective in creation of formulas for mathematical constants because each such formula must be correct for infinite digits of precision, with "near-true" formulas providing no insight toward the correct ones. Consequently, formula discovery lacks a clear distance metric needed to guide automated discovery in this realm. In this work, we propose a systematic methodology for categorization, characterization, and pattern identification of such formulas. The key to our methodology is introducing metrics based on the convergence dynamics of the formulas, rather than on the numerical value of the formula. These metrics enable the first automated clustering of mathematical formulas. We demonstrate this methodology on Polynomial Continued Fraction formulas, which are ubiquitous in their intrinsic connections to mathematical constants, and generalize many mathematical functions and structures. We test our methodology on a set of 1,768,900 such formulas, identifying many known formulas for mathematical constants, and discover previously unknown formulas for $\pi$, $\ln(2)$, Gauss', and Lemniscate's constants. The uncovered patterns enable a direct generalization of individual formulas to infinite families, unveiling rich mathematical structures. This success paves the way towards a generative model that creates formulas fulfilling specified mathematical properties, accelerating the rate of discovery of useful formulas.

The Ramanujan Library -- Automated Discovery on the Hypergraph of Integer Relations

Fundamental mathematical constants appear in nearly every field of science, from physics to biology. Formulas that connect different constants often bring great insight by hinting at connections between previously disparate fields. Discoveries of such relations, however, have remained scarce events, relying on sporadic strokes of creativity by human mathematicians. Recent developments of algorithms for automated conjecture generation have accelerated the discovery of formulas for specific constants. Yet, the discovery of connections between constants has not been addressed. In this paper, we present the first library dedicated to mathematical constants and their interrelations. This library can serve as a central repository of knowledge for scientists from different areas, and as a collaborative platform for development of new algorithms. The library is based on a new representation that we propose for organizing the formulas of mathematical constants: a hypergraph, with each node representing a constant and each edge representing a formula. Using this representation, we propose and demonstrate a systematic approach for automatically enriching this library using PSLQ, an integer relation algorithm based on QR decomposition and lattice construction. During its development and testing, our strategy led to the discovery of 75 previously unknown connections between constants, including a new formula for the `first continued fraction' constant $C_1$, novel formulas for natural logarithms, and new formulas connecting $\pi$ and $e$. The latter formulas generalize a century-old relation between $\pi$ and $e$ by Ramanujan, which until now was considered a singular formula and is now found to be part of a broader mathematical structure. The code supporting this library is a public, open-source API that can serve researchers in experimental mathematics and other fields of science.

Algorithm-assisted discovery of an intrinsic order among mathematical constants

In recent decades, a growing number of discoveries in fields of mathematics have been assisted by computer algorithms, primarily for exploring large parameter spaces that humans would take too long to investigate. As computers and algorithms become more powerful, an intriguing possibility arises - the interplay between human intuition and computer algorithms can lead to discoveries of novel mathematical concepts that would otherwise remain elusive. To realize this perspective, we have developed a massively parallel computer algorithm that discovers an unprecedented number of continued fraction formulas for fundamental mathematical constants. The sheer number of formulas discovered by the algorithm unveils a novel mathematical structure that we call the conservative matrix field. Such matrix fields (1) unify thousands of existing formulas, (2) generate infinitely many new formulas, and most importantly, (3) lead to unexpected relations between different mathematical constants, including multiple integer values of the Riemann zeta function. Conservative matrix fields also enable new mathematical proofs of irrationality. In particular, we can use them to generalize the celebrated proof by Ap\'ery for the irrationality of $\zeta(3)$. Utilizing thousands of personal computers worldwide, our computer-supported research strategy demonstrates the power of experimental mathematics, highlighting the prospects of large-scale computational approaches to tackle longstanding open problems and discover unexpected connections across diverse fields of science.

Automated Search for Conjectures on Mathematical Constants using Analysis of Integer Sequences

Formulas involving fundamental mathematical constants had a great impact on various fields of science and mathematics, for example aiding in proofs of irrationality of constants. However, the discovery of such formulas has historically remained scarce, often perceived as an act of mathematical genius by great mathematicians such as Ramanujan, Euler, and Gauss. Recent efforts to automate the discovery of formulas for mathematical constants, such as the Ramanujan Machine project, relied on exhaustive search. Despite several successful discoveries, exhaustive search remains limited by the space of options that can be covered and by the need for vast amounts of computational resources. Here we propose a fundamentally different method to search for conjectures on mathematical constants: through analysis of integer sequences. We introduce the Enumerated Signed-continued-fraction Massey Approve (ESMA) algorithm, which builds on the Berlekamp-Massey algorithm to identify patterns in integer sequences that represent mathematical constants. The ESMA algorithm found various known formulas for $e, e^2, tan(1)$, and ratios of values of Bessel functions. The algorithm further discovered a large number of new conjectures for these constants, some providing simpler representations and some providing faster numerical convergence than the corresponding simple continued fractions. Along with the algorithm, we present mathematical tools for manipulating continued fractions. These connections enable us to characterize what space of constants can be found by ESMA and quantify its algorithmic advantage in certain scenarios. Altogether, this work continues in the development of augmenting mathematical intuition by computer algorithms, to help reveal mathematical structures and accelerate mathematical research.

The Ramanujan Machine: Automatically Generated Conjectures on Fundamental Constants

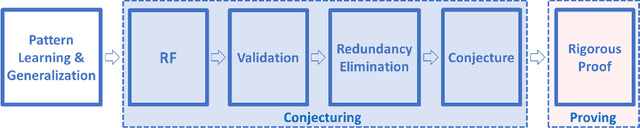
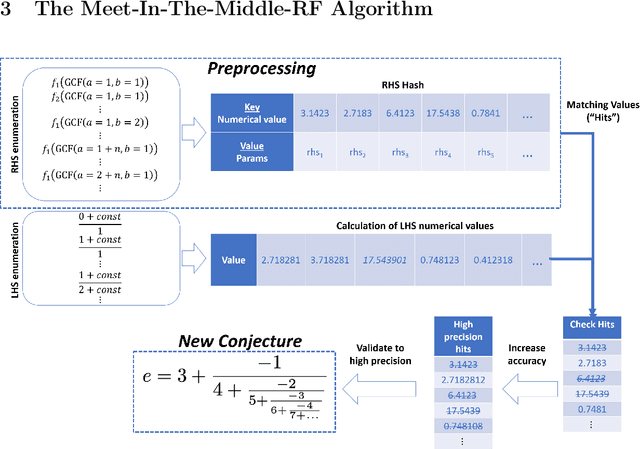
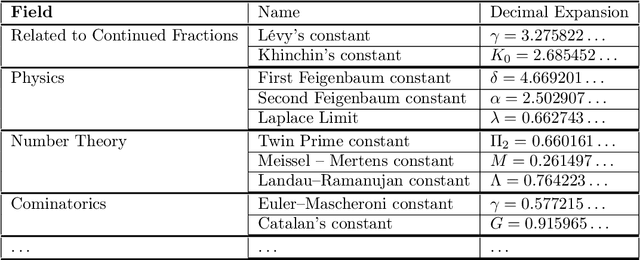
Fundamental mathematical constants like $e$ and $\pi$ are ubiquitous in diverse fields of science, from abstract mathematics and geometry to physics, biology and chemistry. Nevertheless, for centuries new mathematical formulas relating fundamental constants have been scarce and usually discovered sporadically. In this paper we propose a novel and systematic approach that leverages algorithms for deriving mathematical formulas for fundamental constants and help reveal their underlying structure. Our algorithms find dozens of well-known as well as previously unknown continued fraction representations of $\pi$, $e$, and the Riemann zeta function values. Two conjectures produced by our algorithm, along with many others, are: \begin{equation*} \frac{e}{e-2} = 4 - \frac{1}{5-\frac{2}{6-\frac{3}{7-\frac{4}{8-\ldots}}}} \quad\quad,\quad\quad \frac{4}{3\pi-8} = 3-\frac{1\cdot1}{6-\frac{2\cdot3}{9-\frac{3\cdot5}{12-\frac{4\cdot 7}{15-\ldots}}}} \end{equation*} We present two algorithms that proved useful in finding conjectures: a variant of the Meet-In-The-Middle (MITM) algorithm and a Gradient Descent (GD) tailored to the recurrent structure of continued fractions. Both algorithms are based on matching numerical values and thus they conjecture formulas without providing proofs and without requiring any prior knowledge on any underlaying mathematical structure. This approach is especially attractive for fundamental constants for which no mathematical structure is known, as it reverses the conventional approach of sequential logic in formal proofs. Instead, our work supports a different conceptual approach for research: computer algorithms utilizing numerical data to unveil mathematical structures, thus trying to play the role of intuition of great mathematicians of the past, providing leads to new mathematical research.