Case-based similar image retrieval for weakly annotated large histopathological images of malignant lymphoma using deep metric learning

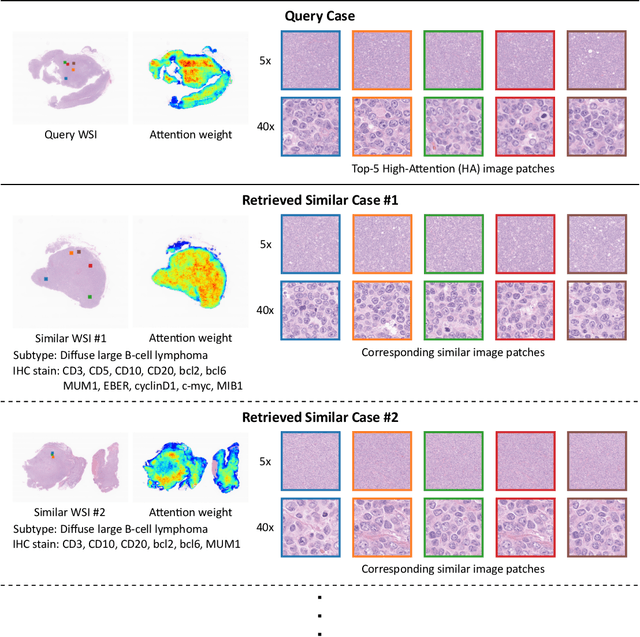
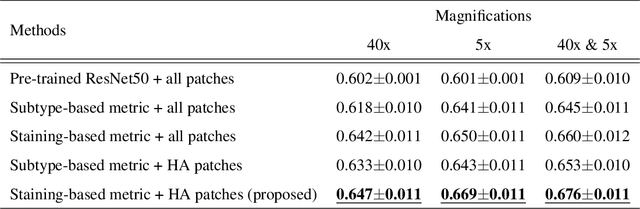
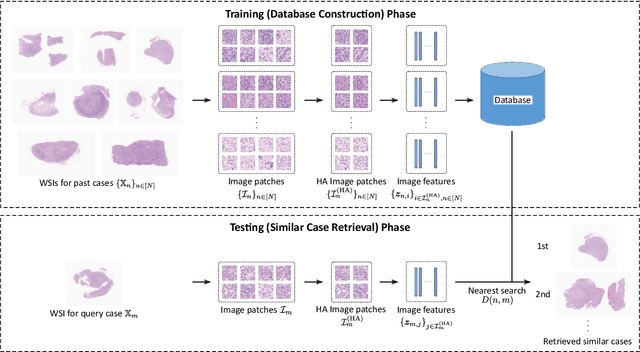
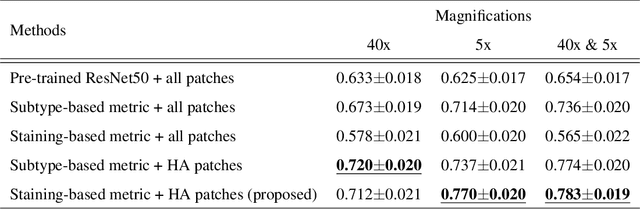
In the present study, we propose a novel case-based similar image retrieval (SIR) method for hematoxylin and eosin (H&E)-stained histopathological images of malignant lymphoma. When a whole slide image (WSI) is used as an input query, it is desirable to be able to retrieve similar cases by focusing on image patches in pathologically important regions such as tumor cells. To address this problem, we employ attention-based multiple instance learning, which enables us to focus on tumor-specific regions when the similarity between cases is computed. Moreover, we employ contrastive distance metric learning to incorporate immunohistochemical (IHC) staining patterns as useful supervised information for defining appropriate similarity between heterogeneous malignant lymphoma cases. In the experiment with 249 malignant lymphoma patients, we confirmed that the proposed method exhibited higher evaluation measures than the baseline case-based SIR methods. Furthermore, the subjective evaluation by pathologists revealed that our similarity measure using IHC staining patterns is appropriate for representing the similarity of H&E-stained tissue images for malignant lymphoma.

Fast and More Powerful Selective Inference for Sparse High-order Interaction Model

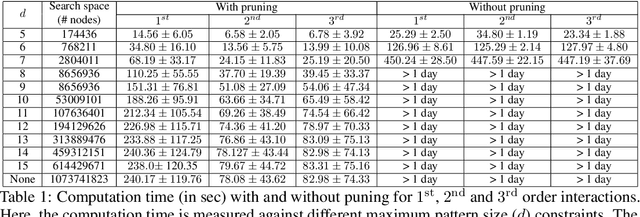
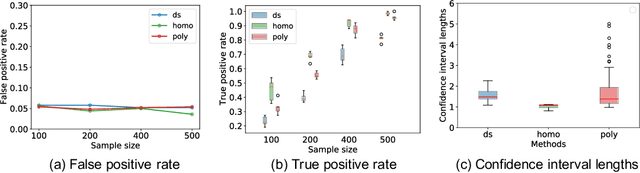
Automated high-stake decision-making such as medical diagnosis requires models with high interpretability and reliability. As one of the interpretable and reliable models with good prediction ability, we consider Sparse High-order Interaction Model (SHIM) in this study. However, finding statistically significant high-order interactions is challenging due to the intrinsic high dimensionality of the combinatorial effects. Another problem in data-driven modeling is the effect of "cherry-picking" a.k.a. selection bias. Our main contribution is to extend the recently developed parametric programming approach for selective inference to high-order interaction models. Exhaustive search over the cherry tree (all possible interactions) can be daunting and impractical even for a small-sized problem. We introduced an efficient pruning strategy and demonstrated the computational efficiency and statistical power of the proposed method using both synthetic and real data.

More Powerful Conditional Selective Inference for Generalized Lasso by Parametric Programming

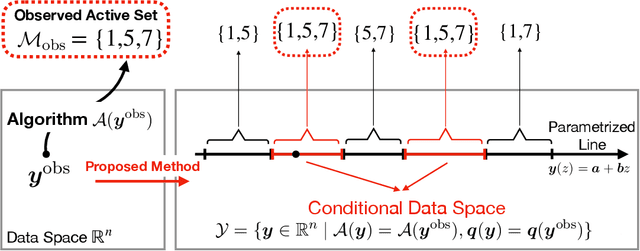
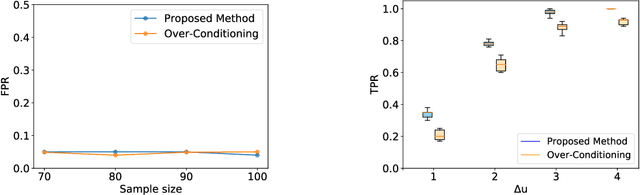
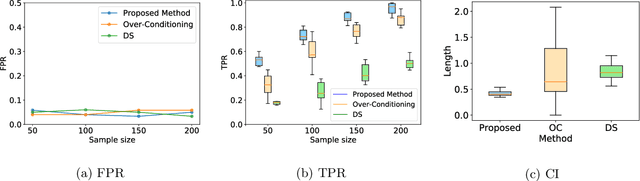
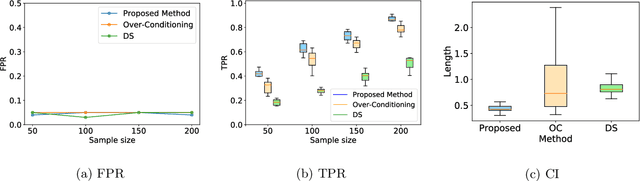
Conditional selective inference (SI) has been studied intensively as a new statistical inference framework for data-driven hypotheses. The basic concept of conditional SI is to make the inference conditional on the selection event, which enables an exact and valid statistical inference to be conducted even when the hypothesis is selected based on the data. Conditional SI has mainly been studied in the context of model selection, such as vanilla lasso or generalized lasso. The main limitation of existing approaches is the low statistical power owing to over-conditioning, which is required for computational tractability. In this study, we propose a more powerful and general conditional SI method for a class of problems that can be converted into quadratic parametric programming, which includes generalized lasso. The key concept is to compute the continuum path of the optimal solution in the direction of the selected test statistic and to identify the subset of the data space that corresponds to the model selection event by following the solution path. The proposed parametric programming-based method not only avoids the aforementioned major drawback of over-conditioning, but also improves the performance and practicality of SI in various respects. We conducted several experiments to demonstrate the effectiveness and efficiency of our proposed method.

Conditional Selective Inference for Robust Regression and Outlier Detection using Piecewise-Linear Homotopy Continuation

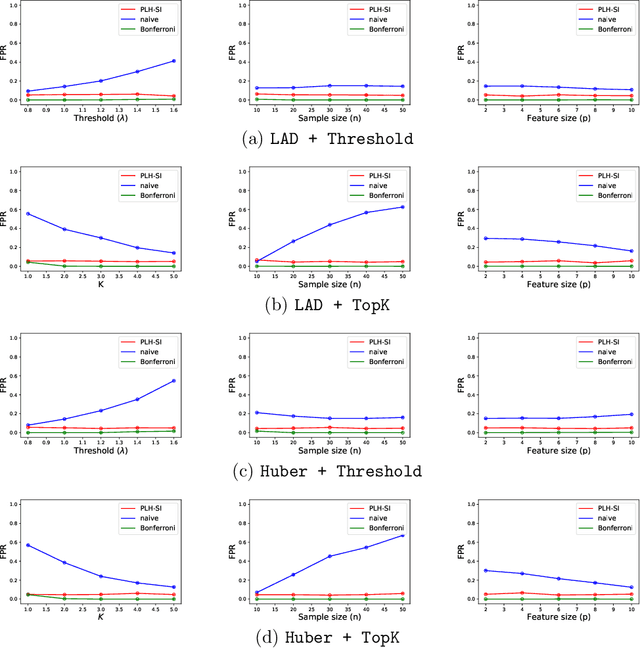
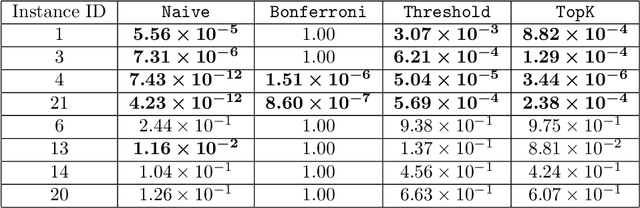
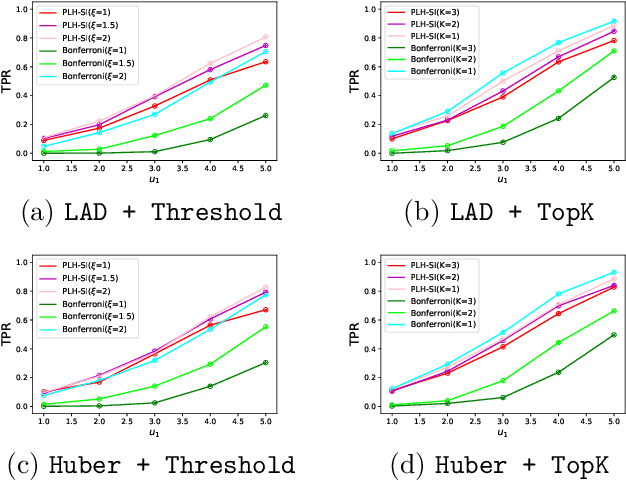
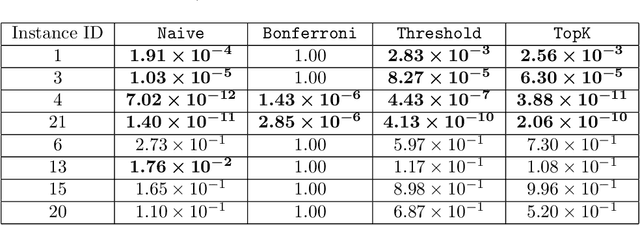
In practical data analysis under noisy environment, it is common to first use robust methods to identify outliers, and then to conduct further analysis after removing the outliers. In this paper, we consider statistical inference of the model estimated after outliers are removed, which can be interpreted as a selective inference (SI) problem. To use conditional SI framework, it is necessary to characterize the events of how the robust method identifies outliers. Unfortunately, the existing methods cannot be directly used here because they are applicable to the case where the selection events can be represented by linear/quadratic constraints. In this paper, we propose a conditional SI method for popular robust regressions by using homotopy method. We show that the proposed conditional SI method is applicable to a wide class of robust regression and outlier detection methods and has good empirical performance on both synthetic data and real data experiments.

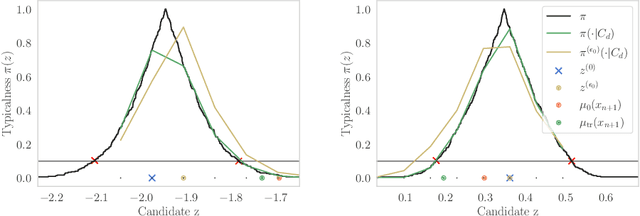
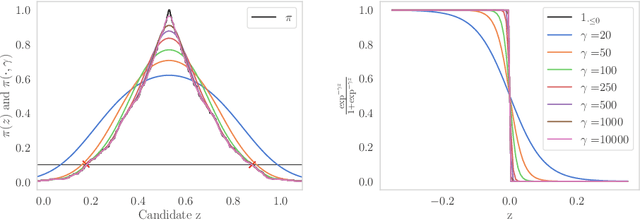
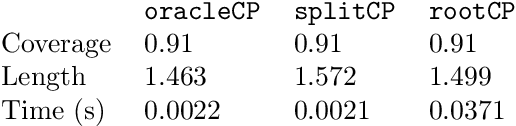
Root-finding Approaches for Computing Conformal Prediction Set

Conformal prediction constructs a confidence region for an unobserved response of a feature vector based on previous identically distributed and exchangeable observations of responses and features. It has a coverage guarantee at any nominal level without additional assumptions on their distribution. However, it requires a refitting procedure for all replacement candidates of the target response. In regression settings, this corresponds to an infinite number of model fit. Apart from relatively simple estimators that can be written as pieces of linear function of the response, efficiently computing such sets is difficult and is still considered as an open problem. We exploit the fact that, \emph{often}, conformal prediction sets are intervals whose boundaries can be efficiently approximated by classical root-finding software. We investigate how this approach can overcome many limitations of formerly used strategies and achieves calculations that have been unattainable so far. We discuss its complexity as well as its drawbacks and evaluate its efficiency through numerical experiments.

Active learning for distributionally robust level-set estimation

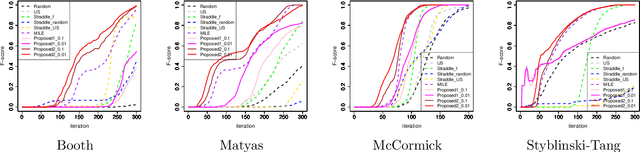
Many cases exist in which a black-box function $f$ with high evaluation cost depends on two types of variables $\bm x$ and $\bm w$, where $\bm x$ is a controllable \emph{design} variable and $\bm w$ are uncontrollable \emph{environmental} variables that have random variation following a certain distribution $P$. In such cases, an important task is to find the range of design variables $\bm x$ such that the function $f(\bm x, \bm w)$ has the desired properties by incorporating the random variation of the environmental variables $\bm w$. A natural measure of robustness is the probability that $f(\bm x, \bm w)$ exceeds a given threshold $h$, which is known as the \emph{probability threshold robustness} (PTR) measure in the literature on robust optimization. However, this robustness measure cannot be correctly evaluated when the distribution $P$ is unknown. In this study, we addressed this problem by considering the \textit{distributionally robust PTR} (DRPTR) measure, which considers the worst-case PTR within given candidate distributions. Specifically, we studied the problem of efficiently identifying a reliable set $H$, which is defined as a region in which the DRPTR measure exceeds a certain desired probability $\alpha$, which can be interpreted as a level set estimation (LSE) problem for DRPTR. We propose a theoretically grounded and computationally efficient active learning method for this problem. We show that the proposed method has theoretical guarantees on convergence and accuracy, and confirmed through numerical experiments that the proposed method outperforms existing methods.

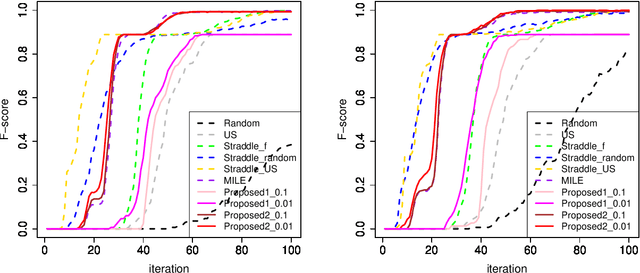
More Powerful and General Selective Inference for Stepwise Feature Selection using the Homotopy Continuation Approach

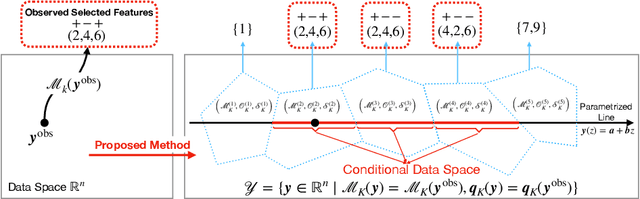
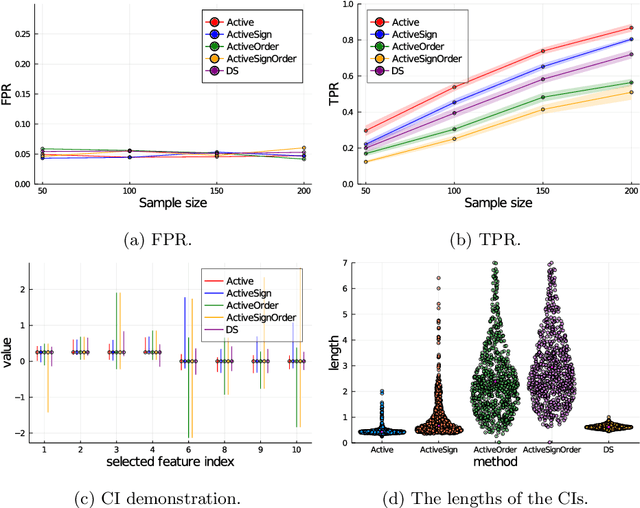
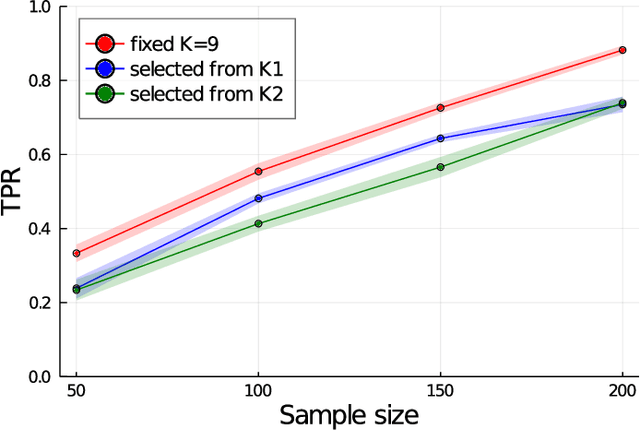
Conditional Selective Inference (SI) has been actively studied as a new statistical inference framework for data-driven hypotheses. For example, conditional SI framework enables exact (non-asymptotic) inference on the features selected by stepwise feature selection (SFS) method. The basic idea of conditional SI is to make inference conditional on the selection event. The main limitation of existing conditional SI approach for SFS method is the loss of power due to over-conditioning for computational tractability. In this paper, we develop more powerful and general conditional SI method for SFS by resolving the over-conditioning issue by homotopy continuation approach. We conduct several experiments to demonstrate the effectiveness and efficiency of our proposed method.

Supervised sequential pattern mining of event sequences in sport to identify important patterns of play: an application to rugby union

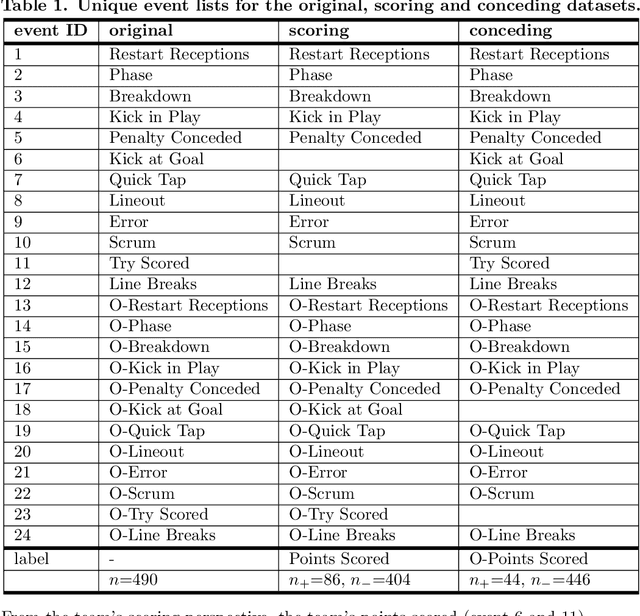
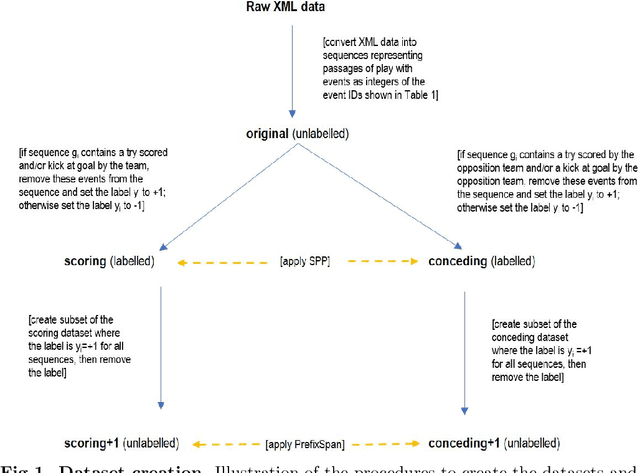
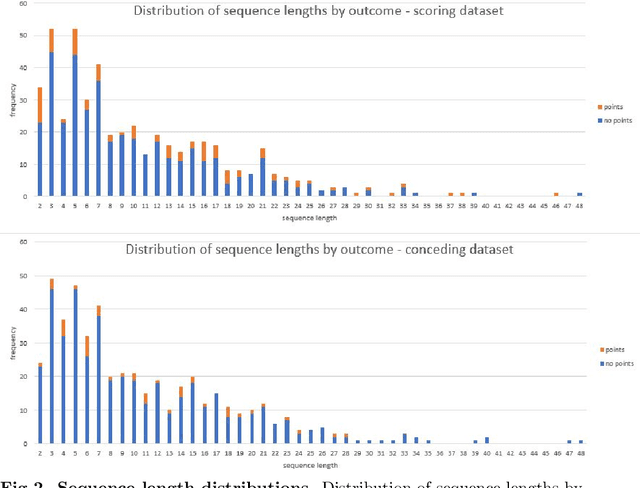
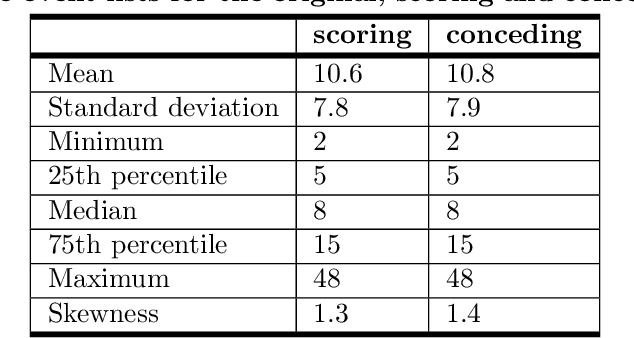
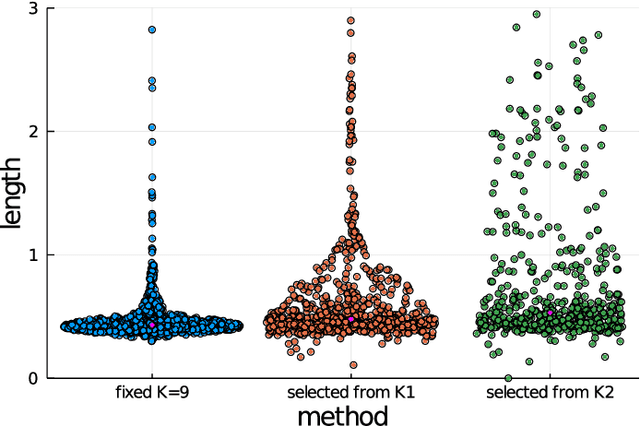
Given a set of sequences comprised of time-ordered events, sequential pattern mining is useful to identify frequent sub-sequences from different sequences or within the same sequence. However, in sport, these techniques cannot determine the importance of particular patterns of play to good or bad outcomes, which is often of greater interest to coaches. In this study, we apply a supervised sequential pattern mining algorithm called safe pattern pruning (SPP) to 490 labelled event sequences representing passages of play from one rugby team's matches from the 2018 Japan Top League, and then evaluate the importance of the obtained sub-sequences to points-scoring outcomes. Linebreaks, successful lineouts, regained kicks in play, repeated phase-breakdown play, and failed opposition exit plays were identified as important patterns of play for the team scoring. When sequences were labelled with points scoring outcomes for the opposition teams, opposition team linebreaks, errors made by the team, opposition team lineouts, and repeated phase-breakdown play by the opposition team were identified as important patterns of play for the opposition team scoring. By virtue of its supervised nature and pruning properties, SPP obtained a greater variety of generally more sophisticated patterns than the well-known unsupervised PrefixSpan algorithm.

Quantifying Statistical Significance of Neural Network Representation-Driven Hypotheses by Selective Inference

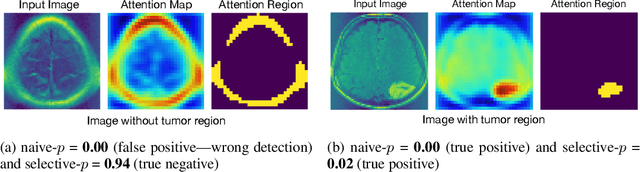
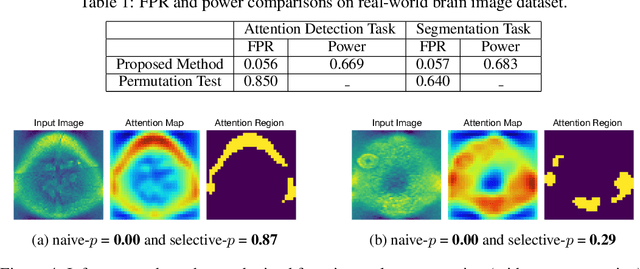
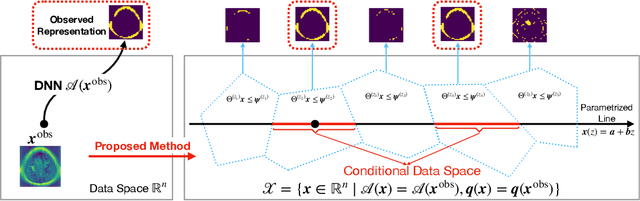
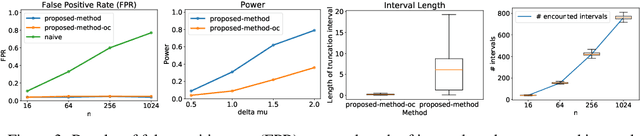
In the past few years, various approaches have been developed to explain and interpret deep neural network (DNN) representations, but it has been pointed out that these representations are sometimes unstable and not reproducible. In this paper, we interpret these representations as hypotheses driven by DNN (called DNN-driven hypotheses) and propose a method to quantify the reliability of these hypotheses in statistical hypothesis testing framework. To this end, we introduce Selective Inference (SI) framework, which has received much attention in the past few years as a new statistical inference framework for data-driven hypotheses. The basic idea of SI is to make conditional inferences on the selected hypotheses under the condition that they are selected. In order to use SI framework for DNN representations, we develop a new SI algorithm based on homotopy method which enables us to derive the exact (non-asymptotic) conditional sampling distribution of the DNN-driven hypotheses. We conduct experiments on both synthetic and real-world datasets, through which we offer evidence that our proposed method can successfully control the false positive rate, has decent performance in terms of computational efficiency, and provides good results in practical applications.

Mean-Variance Analysis in Bayesian Optimization under Uncertainty

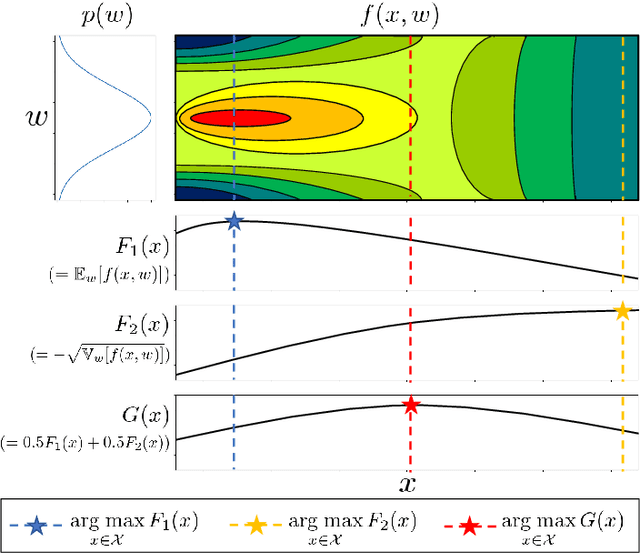
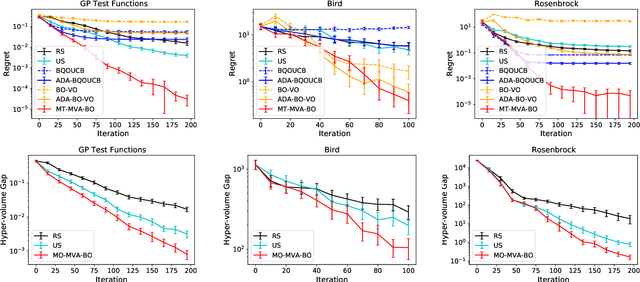
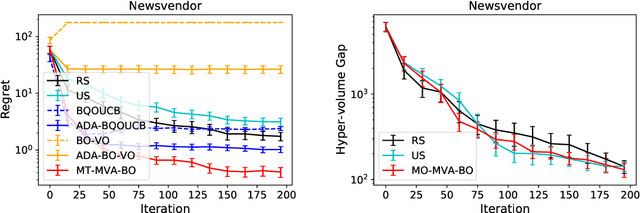
We consider active learning (AL) in an uncertain environment in which trade-off between multiple risk measures need to be considered. As an AL problem in such an uncertain environment, we study Mean-Variance Analysis in Bayesian Optimization (MVA-BO) setting. Mean-variance analysis was developed in the field of financial engineering and has been used to make decisions that take into account the trade-off between the average and variance of investment uncertainty. In this paper, we specifically focus on BO setting with an uncertain component and consider multi-task, multi-objective, and constrained optimization scenarios for the mean-variance trade-off of the uncertain component. When the target blackbox function is modeled by Gaussian Process (GP), we derive the bounds of the two risk measures and propose AL algorithm for each of the above three problems based on the risk measure bounds. We show the effectiveness of the proposed AL algorithms through theoretical analysis and numerical experiments.