Phase Transitions with Structured Sparsity

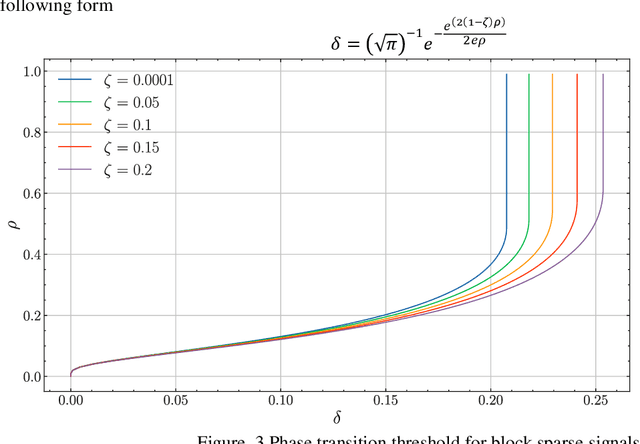
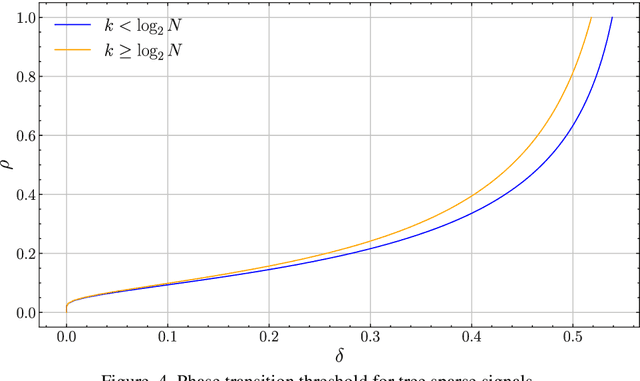
In the field of signal processing, phase transition phenomena have recently attracted great attention. Donoho's work established the signal recovery threshold using indicators such as restricted isotropy (RIP) and incoherence and proved that phase transition phenomena occur in compressed sampling. Nevertheless, the phase transition phenomenon of structured sparse signals remains unclear, and these studies mainly focused on simple sparse signals. Signals with a specific structure, such as the block or tree structures common in real-world applications, are called structured sparse signals. The objectives of this article are to study the phase transition phenomenon of structured sparse signals and to investigate how structured sparse signals affect the phase transition threshold. It begins with a summary of the common subspace of structured sparse signals and the theory of high-dimensional convex polytope random projections. Next, the strong threshold expression of block-structured and tree-structured sparse signals is derived after examining the weak and strong thresholds of structured sparse signals.

Windowed Compressed Spectrum Sensing with Block sparsity

Compressed Spectrum Sensing (CSS) is widely employed in spectral analysis due to its sampling efficiency. However, conventional CSS assumes a standard sparse spectrum, which is affected by Spectral Leakage (SL). Despite the widespread use of CSS, the impact of SL on its performance has not been systematically and thoroughly investigated. This study addresses this research gap by analyzing the Restricted Isometry Property (RIP) of windowed Gaussian measurement matrices and proposing a novel block-sparse CSS model. We introduce the Edge Zeroing Coefficient (EZC) to evaluate SL suppression and RIP impact, and the Window Scaling Coefficient (WSC) to quantify the effect on RIP. Our research investigates the influence of Window Function (WF) on signal sparsity and measurement matrices, and presents a block-sparse CSS model that considers component frequency distribution, signal length, windowing, and noise floor. Based on subspace counting theory, we derive sample bound for our model. The findings demonstrate that while WFs reduce SL, excessively small EZC and WSC values can negatively affect RIP quality and cause numerical instability during signal reconstruction. This highlights the delicate balance required when applying WFs in CSS. Our block-sparse approach enables precise compression and reconstruction, particularly for high noise floor and super-sparse signals. This study provides a framework for optimizing CSS performance when dealing with SL and sparse signals, offering insights for improving signal reconstruction quality in various applications