A Minimal Model for Emergent Collective Behaviors in Autonomous Robotic Multi-Agent Systems

Collective behaviors such as swarming and flocking emerge from simple, decentralized interactions in biological systems. Existing models, such as Vicsek and Cucker-Smale, lack collision avoidance, whereas the Olfati-Saber model imposes rigid formations, limiting their applicability in swarm robotics. To address these limitations, this paper proposes a minimal yet expressive model that governs agent dynamics using relative positions, velocities, and local density, modulated by two tunable parameters: the spatial offset and kinetic offset. The model achieves spatially flexible, collision-free behaviors that reflect naturalistic group dynamics. Furthermore, we extend the framework to cognitive autonomous systems, enabling energy-aware phase transitions between swarming and flocking through adaptive control parameter tuning. This cognitively inspired approach offers a robust foundation for real-world applications in multi-robot systems, particularly autonomous aerial swarms.

Distributed Receding Horizon Control of Autonomous Convoy with Self-Interested Vehicles

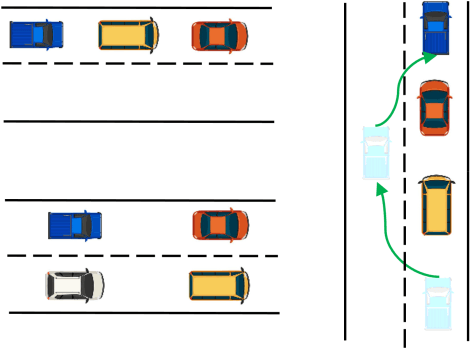
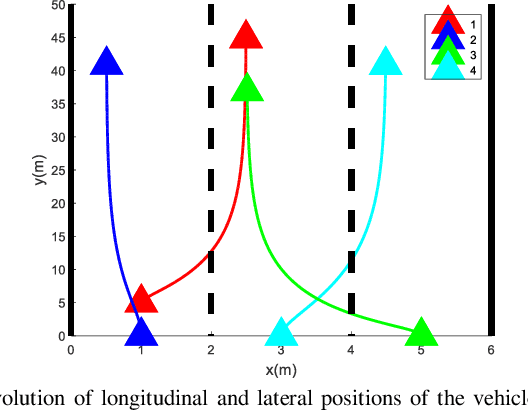
This paper considers the problem of controlling a convoy of autonomous vehicles to be deployed on automated highways. The individual behavior of an autonomous vehicle as an intelligent self-interested decision-maker can be analyzed under a non-cooperative differential game model of the convoy. The receding horizon Nash equilibrium of the linear-quadratic differential game provides a distributed state-feedback control strategy for the convoy. This approach suffers a fundamental issue that neither the existence nor the uniqueness of a Nash equilibrium is guaranteed, so the convoy control. We present a relative dynamics based model of the convoy that carries all the features of the individual dynamics based game model. We show that the relative dynamics model guarantees the existence of the convoy control as well as the asymptotic stability of the closed-loop system. Simulations illustrate the effectiveness of the presented convoy control scheme.