Distributed Nonparametric Function Estimation: Optimal Rate of Convergence and Cost of Adaptation

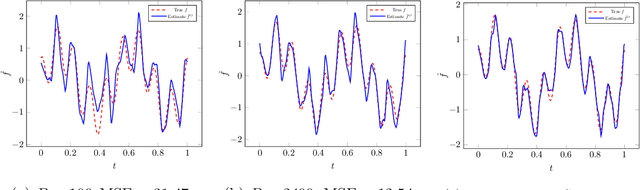
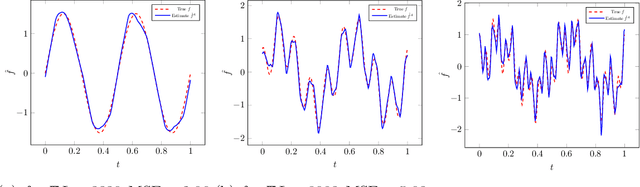
Distributed minimax estimation and distributed adaptive estimation under communication constraints for Gaussian sequence model and white noise model are studied. The minimax rate of convergence for distributed estimation over a given Besov class, which serves as a benchmark for the cost of adaptation, is established. We then quantify the exact communication cost for adaptation and construct an optimally adaptive procedure for distributed estimation over a range of Besov classes. The results demonstrate significant differences between nonparametric function estimation in the distributed setting and the conventional centralized setting. For global estimation, adaptation in general cannot be achieved for free in the distributed setting. The new technical tools to obtain the exact characterization for the cost of adaptation can be of independent interest.

Distributed Gaussian Mean Estimation under Communication Constraints: Optimal Rates and Communication-Efficient Algorithms

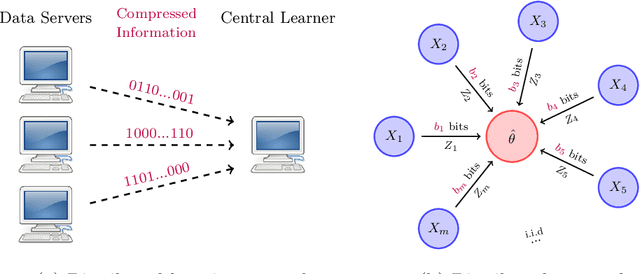
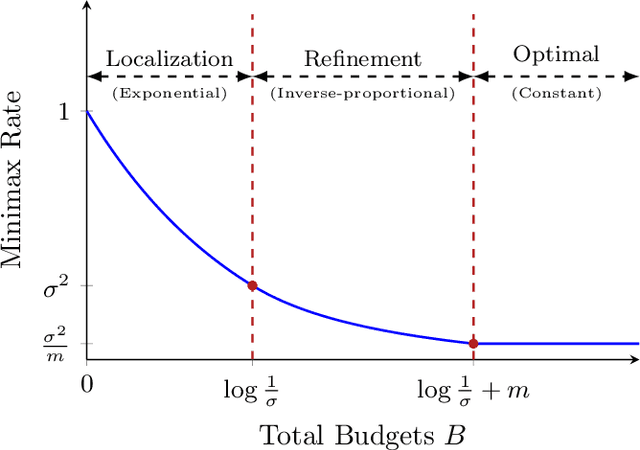
We study distributed estimation of a Gaussian mean under communication constraints in a decision theoretical framework. Minimax rates of convergence, which characterize the tradeoff between the communication costs and statistical accuracy, are established in both the univariate and multivariate settings. Communication-efficient and statistically optimal procedures are developed. In the univariate case, the optimal rate depends only on the total communication budget, so long as each local machine has at least one bit. However, in the multivariate case, the minimax rate depends on the specific allocations of the communication budgets among the local machines. Although optimal estimation of a Gaussian mean is relatively simple in the conventional setting, it is quite involved under the communication constraints, both in terms of the optimal procedure design and lower bound argument. The techniques developed in this paper can be of independent interest. An essential step is the decomposition of the minimax estimation problem into two stages, localization and refinement. This critical decomposition provides a framework for both the lower bound analysis and optimal procedure design.

Transfer Learning for Nonparametric Classification: Minimax Rate and Adaptive Classifier

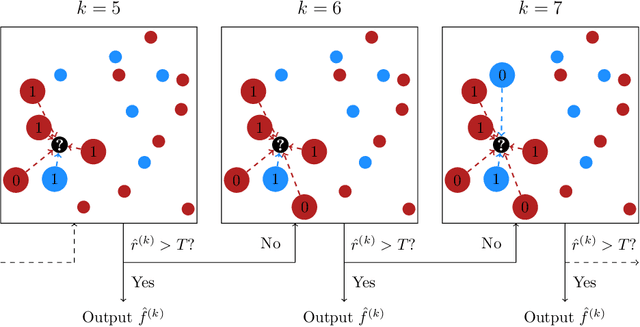
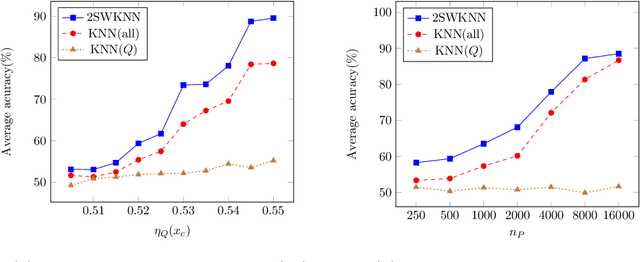
Human learners have the natural ability to use knowledge gained in one setting for learning in a different but related setting. This ability to transfer knowledge from one task to another is essential for effective learning. In this paper, we study transfer learning in the context of nonparametric classification based on observations from different distributions under the posterior drift model, which is a general framework and arises in many practical problems. We first establish the minimax rate of convergence and construct a rate-optimal two-sample weighted $K$-NN classifier. The results characterize precisely the contribution of the observations from the source distribution to the classification task under the target distribution. A data-driven adaptive classifier is then proposed and is shown to simultaneously attain within a logarithmic factor of the optimal rate over a large collection of parameter spaces. Simulation studies and real data applications are carried out where the numerical results further illustrate the theoretical analysis. Extensions to the case of multiple source distributions are also considered.