The Glider Equation for Asymptotic Lenia

Lenia is a continuous extension of Conway's Game of Life that exhibits rich pattern formations including self-propelling structures called gliders. In this paper, we focus on Asymptotic Lenia, a variant formulated as partial differential equations. By utilizing this mathematical formulation, we analytically derive the conditions for glider patterns, which we term the ``Glider Equation.'' We demonstrate that by using this equation as a loss function, gradient descent methods can successfully discover stable glider configurations. This approach enables the optimization of update rules to find novel gliders with specific properties, such as faster-moving variants. We also derive a velocity-free equation that characterizes gliders of any speed, expanding the search space for novel patterns. While many optimized patterns result in transient gliders that eventually destabilize, our approach effectively identifies diverse pattern formations that would be difficult to discover through traditional methods. Finally, we establish connections between Asymptotic Lenia and neural field models, highlighting mathematical relationships that bridge these systems and suggesting new directions for analyzing pattern formation in continuous dynamical systems.

Evolution of Collective AI Beyond Individual Optimization

This study investigates collective behaviors that emerge from a group of homogeneous individuals optimized for a specific capability. We created a group of simple, identical neural network based agents modeled after chemotaxis-driven vehicles that follow pheromone trails and examined multi-agent simulations using clones of these evolved individuals. Our results show that the evolution of individuals led to population differentiation. Surprisingly, we observed that collective fitness significantly changed during later evolutionary stages, despite maintained high individual performance and simplified neural architectures. This decline occurred when agents developed reduced sensor-motor coupling, suggesting that over-optimization of individual agents almost always lead to less effective group behavior. Our research investigates how individual differentiation can evolve through what evolutionary pathways.

Implementation of Lenia as a Reaction-Diffusion System

The relationship between reaction-diffusion (RD) systems, characterized by continuous spatiotemporal states, and cellular automata (CA), marked by discrete spatiotemporal states, remains poorly understood. This paper delves into this relationship through an examination of a recently developed CA known as Lenia. We demonstrate that asymptotic Lenia, a variant of Lenia, can be comprehensively described by differential equations, and, unlike the original Lenia, it is independent of time-step ticks. Further, we establish that this formulation is mathematically equivalent to a generalization of the kernel-based Turing model (KT model). Stemming from these insights, we establish that asymptotic Lenia can be replicated by an RD system composed solely of diffusion and spatially local reaction terms, resulting in the simulated asymptotic Lenia based on an RD system, or "RD Lenia". However, our RD Lenia cannot be construed as a chemical system since the reaction term fails to satisfy mass-action kinetics.

Organization of a Latent Space structure in VAE/GAN trained by navigation data

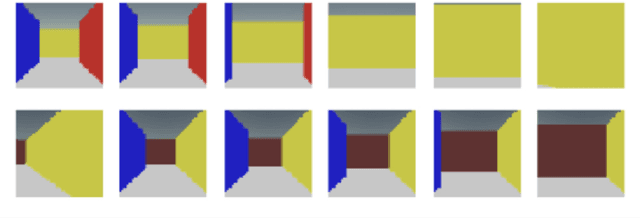
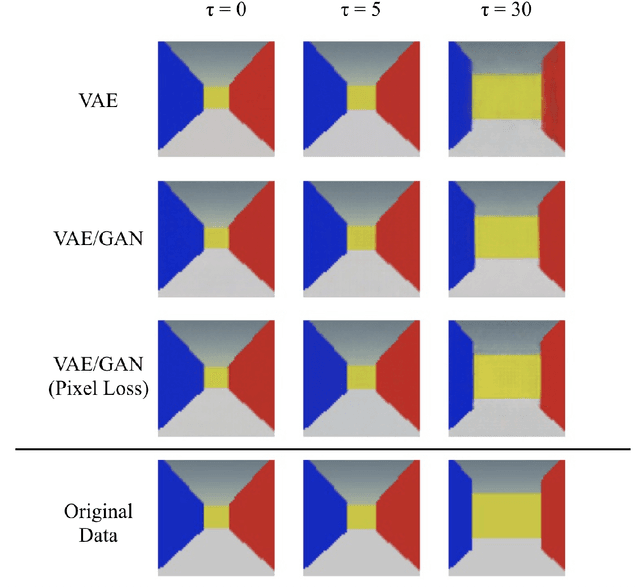
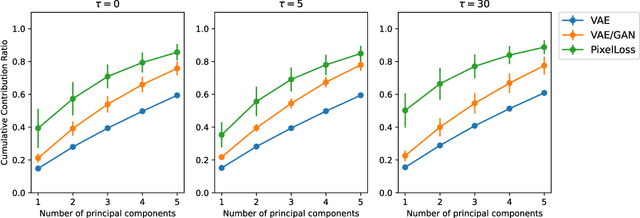
We present a novel artificial cognitive mapping system using generative deep neural networks (VAE/GAN), which can map input images to latent vectors and generate temporal sequences internally. The results show that the distance of the predicted image is reflected in the distance of the corresponding latent vector after training. This indicates that the latent space is constructed to reflect the proximity structure of the data set, and may provide a mechanism by which many aspects of cognition are spatially represented. The present study allows the network to internally generate temporal sequences analogous to hippocampal replay/pre-play, where VAE produces only near-accurate replays of past experiences, but by introducing GANs, latent vectors of temporally close images are closely aligned and sequence acquired some instability. This may be the origin of the generation of the new sequences found in the hippocampus.