Analysing the Influence of Attack Configurations on the Reconstruction of Medical Images in Federated Learning

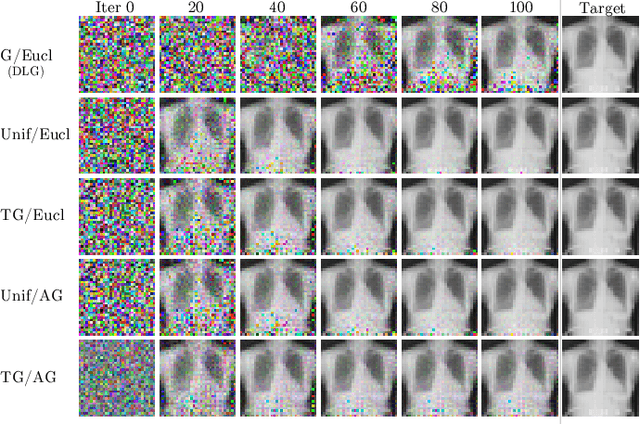
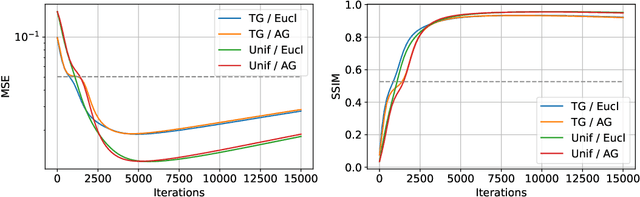
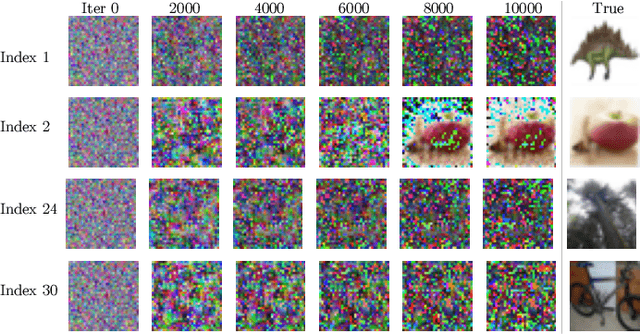
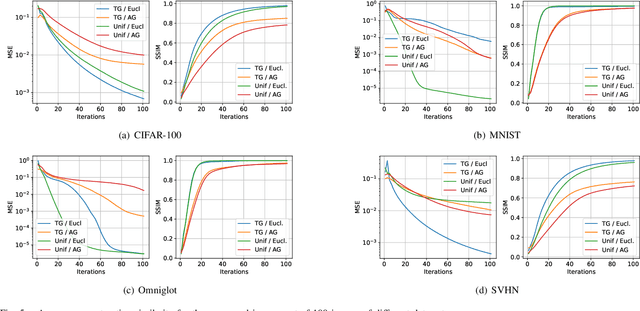
The idea of federated learning is to train deep neural network models collaboratively and share them with multiple participants without exposing their private training data to each other. This is highly attractive in the medical domain due to patients' privacy records. However, a recently proposed method called Deep Leakage from Gradients enables attackers to reconstruct data from shared gradients. This study shows how easy it is to reconstruct images for different data initialization schemes and distance measures. We show how data and model architecture influence the optimal choice of initialization scheme and distance measure configurations when working with single images. We demonstrate that the choice of initialization scheme and distance measure can significantly increase convergence speed and quality. Furthermore, we find that the optimal attack configuration depends largely on the nature of the target image distribution and the complexity of the model architecture.

Machine Learning Assisted Orthonormal Basis Selection for Functional Data Analysis

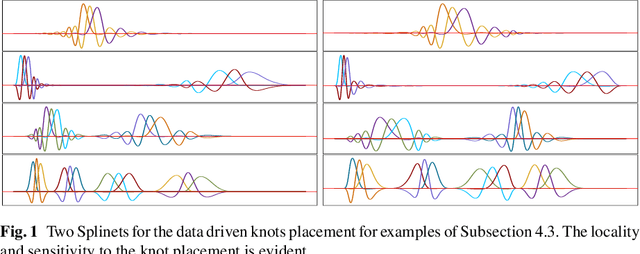
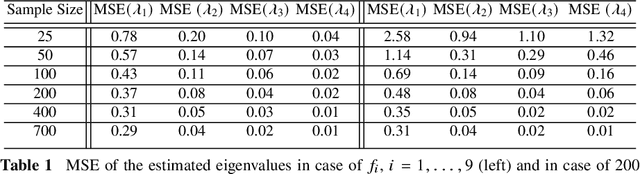
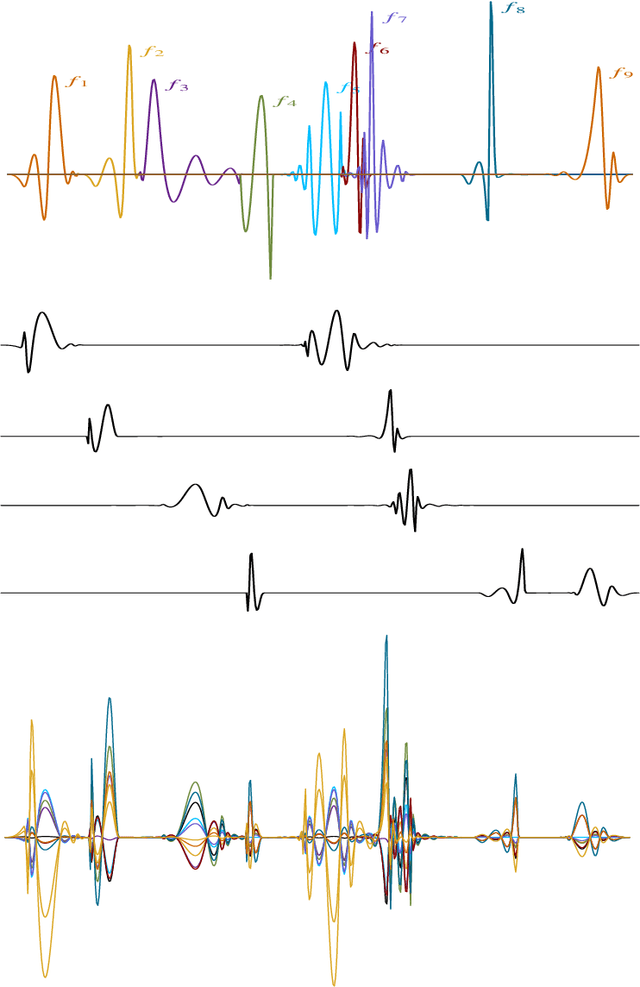
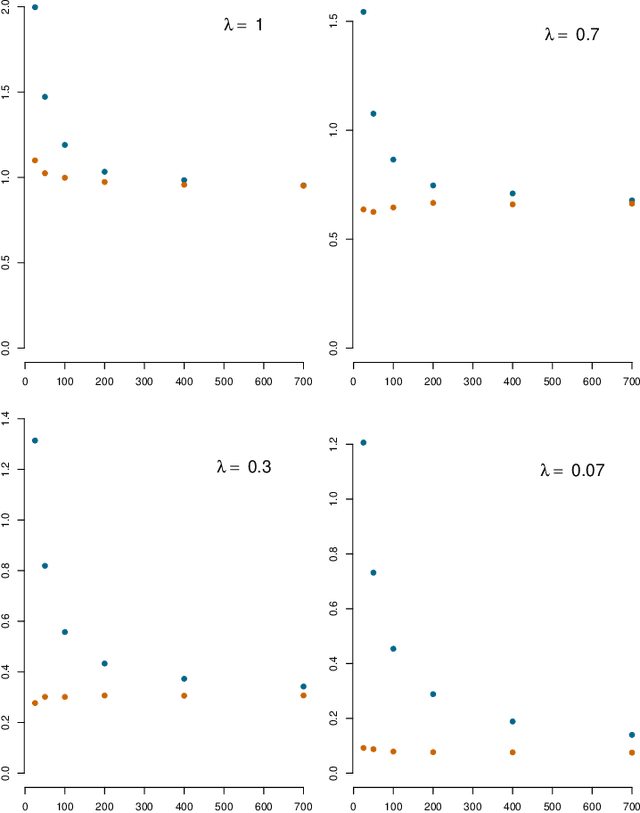
In implementations of the functional data methods, the effect of the initial choice of an orthonormal basis has not gained much attention in the past. Typically, several standard bases such as Fourier, wavelets, splines, etc. are considered to transform observed functional data and a choice is made without any formal criteria indicating which of the bases is preferable for the initial transformation of the data into functions. In an attempt to address this issue, we propose a strictly data-driven method of orthogonal basis selection. The method uses recently introduced orthogonal spline bases called the splinets obtained by efficient orthogonalization of the B-splines. The algorithm learns from the data in the machine learning style to efficiently place knots. The optimality criterion is based on the average (per functional data point) mean square error and is utilized both in the learning algorithms and in comparison studies. The latter indicates efficiency that is particularly evident for the sparse functional data and to a lesser degree in analyses of responses to complex physical systems.