Criticality in Formal Languages and Statistical Physics

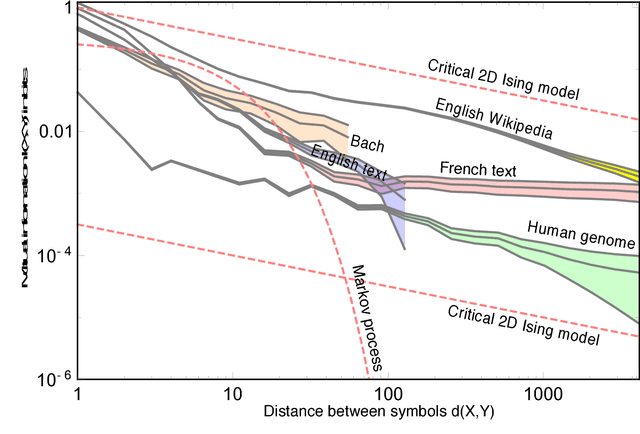
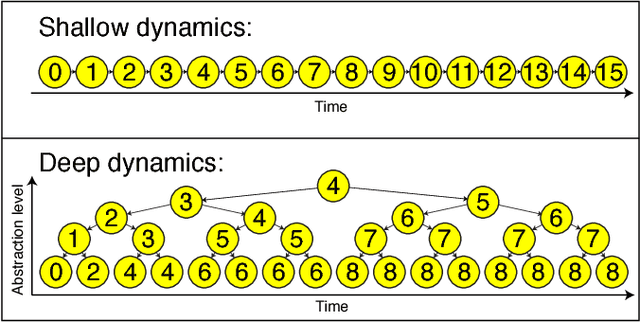
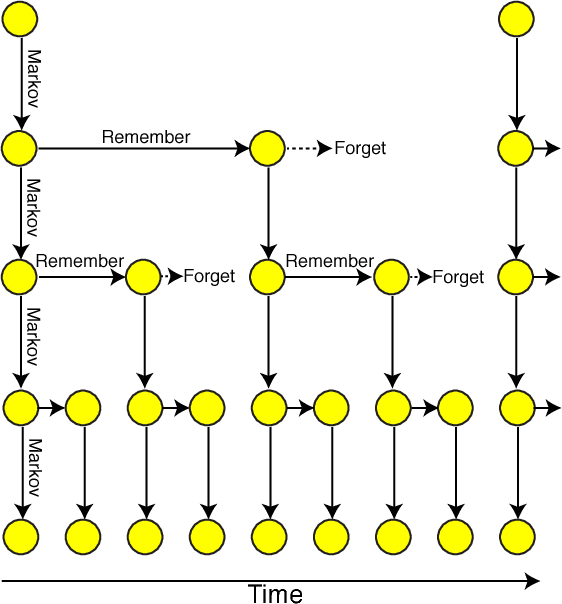
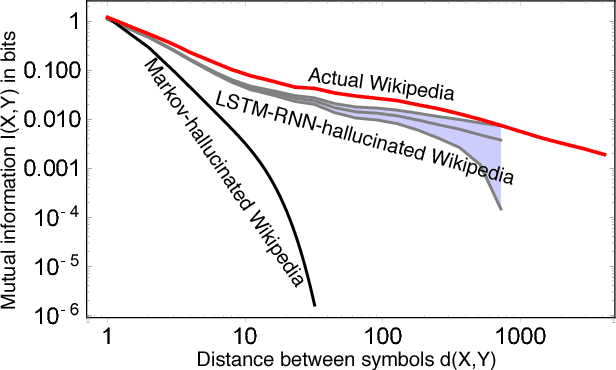
We show that the mutual information between two symbols, as a function of the number of symbols between the two, decays exponentially in any probabilistic regular grammar, but can decay like a power law for a context-free grammar. This result about formal languages is closely related to a well-known result in classical statistical mechanics that there are no phase transitions in dimensions fewer than two. It is also related to the emergence of power-law correlations in turbulence and cosmological inflation through recursive generative processes. We elucidate these physics connections and comment on potential applications of our results to machine learning tasks like training artificial recurrent neural networks. Along the way, we introduce a useful quantity which we dub the rational mutual information and discuss generalizations of our claims involving more complicated Bayesian networks.

Why does deep and cheap learning work so well?

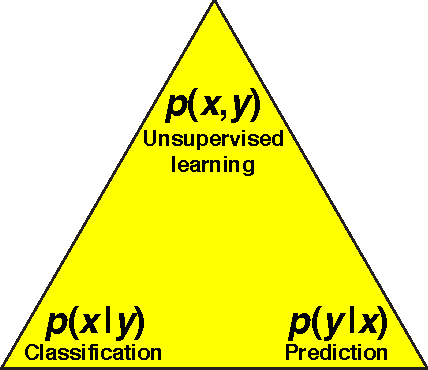
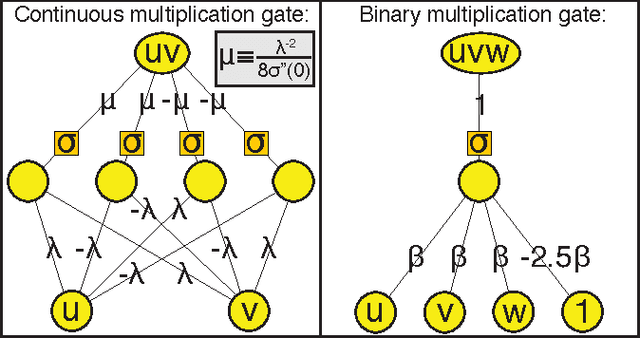
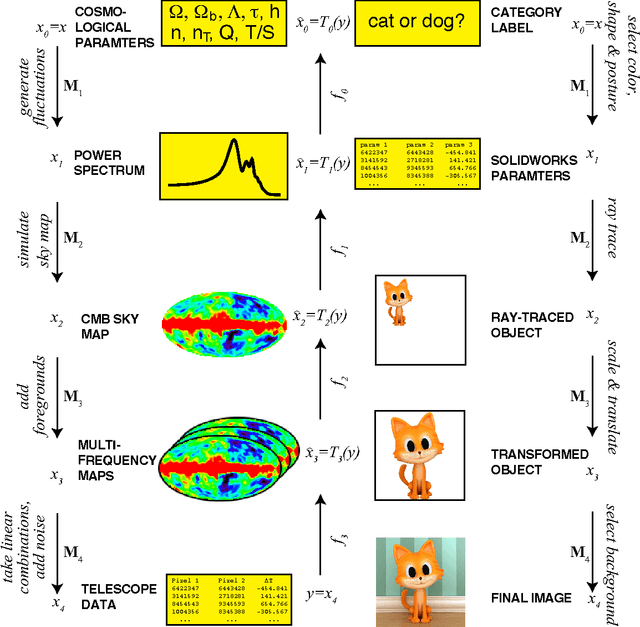
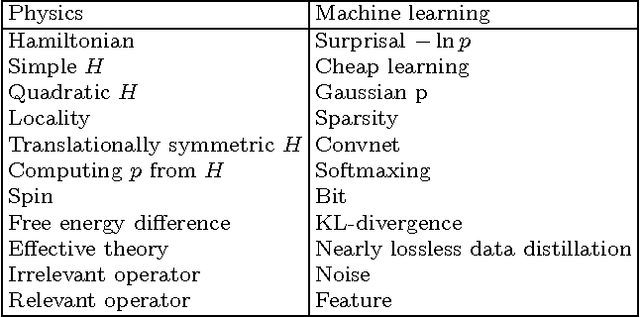
We show how the success of deep learning could depend not only on mathematics but also on physics: although well-known mathematical theorems guarantee that neural networks can approximate arbitrary functions well, the class of functions of practical interest can frequently be approximated through "cheap learning" with exponentially fewer parameters than generic ones. We explore how properties frequently encountered in physics such as symmetry, locality, compositionality, and polynomial log-probability translate into exceptionally simple neural networks. We further argue that when the statistical process generating the data is of a certain hierarchical form prevalent in physics and machine-learning, a deep neural network can be more efficient than a shallow one. We formalize these claims using information theory and discuss the relation to the renormalization group. We prove various "no-flattening theorems" showing when efficient linear deep networks cannot be accurately approximated by shallow ones without efficiency loss, for example, we show that $n$ variables cannot be multiplied using fewer than 2^n neurons in a single hidden layer.