Metrics for Learning in Topological Persistence

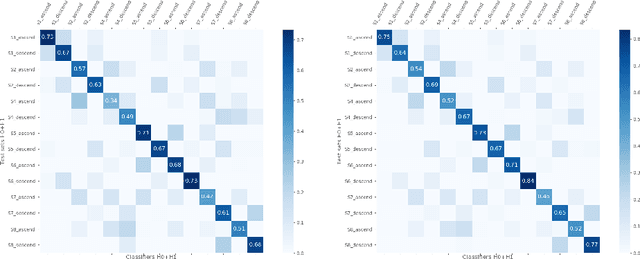
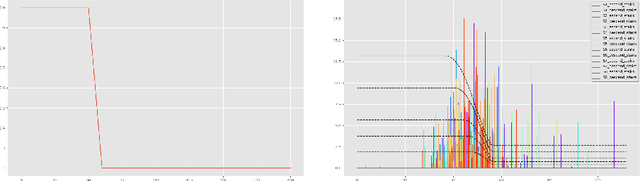
Persistent homology analysis provides means to capture the connectivity structure of data sets in various dimensions. On the mathematical level, by defining a metric between the objects that persistence attaches to data sets, we can stabilize invariants characterizing these objects. We outline how so called contour functions induce relevant metrics for stabilizing the rank invariant. On the practical level, the stable ranks are used as fingerprints for data. Different choices of contour lead to different stable ranks and the topological learning is then the question of finding the optimal contour. We outline our analysis pipeline and show how it can enhance classification of physical activities data. As our main application we study how stable ranks and contours provide robust descriptors of spatial patterns of atmospheric cloud fields.

A topological data analysis based classification method for multiple measurements

Machine learning models for repeated measurements are limited. Using topological data analysis (TDA), we present a classifier for repeated measurements which samples from the data space and builds a network graph based on the data topology. When applying this to two case studies, accuracy exceeds alternative models with additional benefits such as reporting data subsets with high purity along with feature values. For 300 examples of 3 tree species, the accuracy reached 80% after 30 datapoints, which was improved to 90% after increased sampling to 400 datapoints. Using data from 100 examples of each of 6 point processes, the classifier achieved 96.8% accuracy. In both datasets, the TDA classifier outperformed an alternative model. This algorithm and software can be beneficial for repeated measurement data common in biological sciences, as both an accurate classifier and a feature selection tool.